大规模定制生产调度优化模型及其仿真研究——以汽轮机生产为例

王 玉，朱凯燕，成谞虓WANG Yu,ZHU Kai-yan,CHENG Xu-xiao

（1.广东商学院 信息学院，广东 广州 510320；2.同济大学 管理学院，上海 200092）

(1.School of Information Science,Guangdong University of Business Studies,Guangzhou 510320,China;2.School of Economics and Management,Tongji University,Shanghai 200092,China)

0 引 言

大规模定制企业的客户需求多变，如何根据客户的定制需求制定出合适的生产计划，及时对客户需求做出反应是大规模定制企业需要解决的关键问题之一。大规模定制是大规模生产和定制生产的有机结合，其供应链是推式供应链与拉式供应链的结合，即推拉相结合的供应链。推拉供应链的分界点为客户订单分离点 （customer order decoupling point，CODP）。CODP分离的上游计划是基于预测，下游计划是基于订单。这就意味着上游的活动运作可通过主生产计划 （master production schedule，MPS），而下游通过车间调度 （job shop schedule）来管理和控制其生产活动[1]。由于MPS调度问题通常存在众多的约束，使之成为非常难解的NP完全性复杂的优化问题。本文就结合广州某大规模定制企业的汽轮机生产过程，建立大规模定制企业的生产调度优化模型，并用粒子群算法进行了求解。

1 大规模定制的生产调度模型

大规模定制供应链中，CODP定位处是基于预测与基于订单驱动生产的结合，在特定的时期内，产品种类、数量都是动态变化的，具有不确定性。但是，由于产品结构的模块化、规范化，使得其生产在一定程度上呈现出工艺的相似性与产品的同质性，这样该节点的生产在一段时期具有一定的连续性及相关性，如生产主要集中在几种产品上，而其到达时间与需求量是不确定的。因此该节点的生产任务通常由两部分组成，一是基于预测的已有任务，二是随机到来的订单，但随机到来的订单产品又具有一定的规律性。因此，要根据大规模定制的特性来安排订单的生产。大规模定制中，客户一旦下订单，就要在承诺的时间内提交产品和服务。交货时间的变动是按一定时间周期的，如交货时间是n天、n周、n月等，其变动周期为天、周、月。因此，必然有很多订单的交货期在同一周期内。如同一天，同一周，或同一月。由于在同一周期内交货，对这些订单的生产就可以按优化的生产顺序，而不是按下订单的先后顺序。把同一周期内的订单生产的优化，称为同一时间窗口的优化。而跨周期的生产订单，由于交货期的限制，因此，必须先下订单的先生产。下面针对同一时间窗口的订单进行调度分析。

大规模定制生产商将同一时间窗口T内接到的订单进行分类、合并，并对生产过程进行调度。调度过程包括企业任务排序及各子任务开工时间确定。这里调度的例子是某MC机械厂汽轮机的生产过程。汽轮机是技术密集型产品，产品结构比较复杂，可靠性要求很高，主要零部件要求耐高温、耐冲击和高精度。平均每台汽轮机有近5000个零部件。汽轮机的BOM有多层结构，这里主要分析两层。第一层主要由汽缸、油箱底盘、主汽门、前轴承座、前轴承、汽封管路、调节阀、转子部套、隔板部套组成。第二层中汽缸主要由前汽缸、后汽缸、管接头组成；油箱底盘主要由滤网、通汽装置、盖板组成；主汽门主要由管接头、滤网组成；前轴承座主要由盖、除汽器组成；前轴承主要由轴承盖、前径向轴承瓦组成；汽封管路主要由前汽封、排汽管组成；转子部套核心是转子，由汽封环、白铜丝、接长轴、螺钉、螺栓、销等组成；隔板部套主要由隔板1A、隔板2A、隔板3A组成。汽轮机采用了组合产品的设计原理，将产品分解成不同的标准模块，如同搭积木一样，可以根据客户的个性化需求，将有限数量的标准模块组合起来，形成不同的定制产品。如图1是一种汽轮机的定制产品图。

该厂汽轮机的生产主要有5个车间组成，隔板车间、汽缸车间、转子装配车间、箱体车间和总装车间。对汽轮机的生产加工点进行简化后，可以用图2来表示汽轮机的整个生产过程。

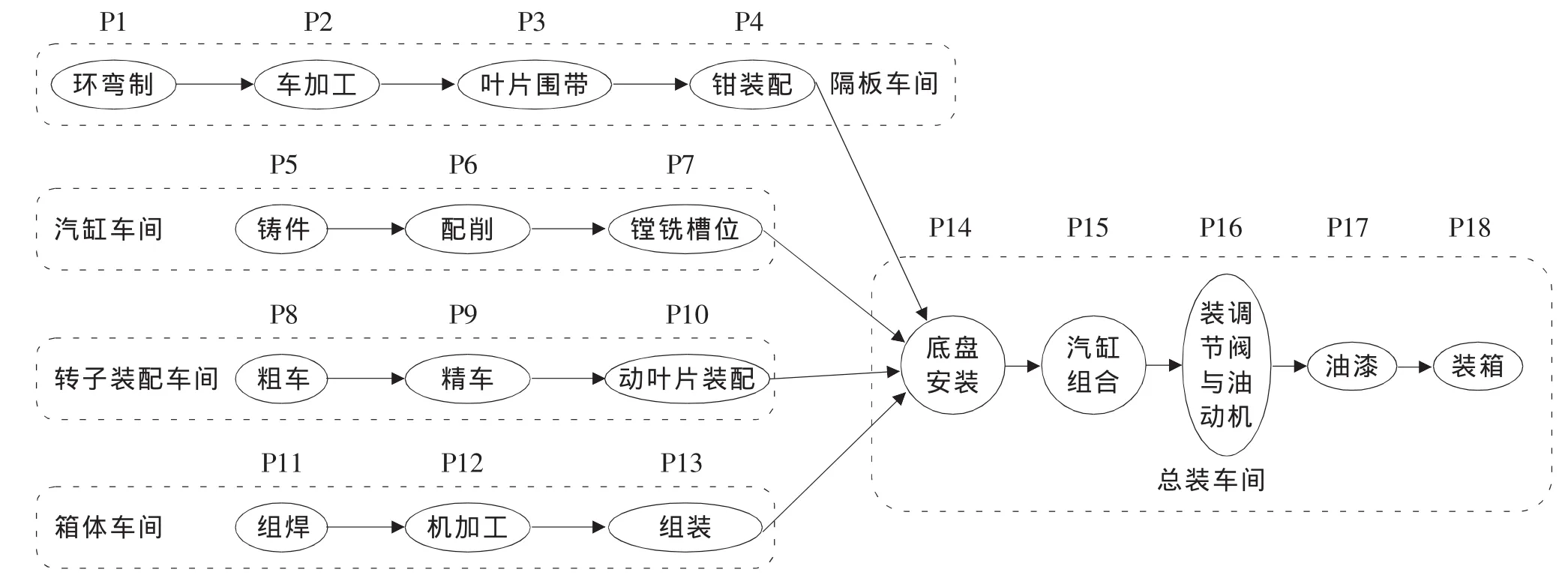
图2 汽轮机的生产链

根据图2，可以将汽轮机的生产根据某类定制订单的生产分解为18个子任务。其中隔板车间的子任务经过P1、P2、P3、P4的加工过程；汽缸车间的子任务经过P5、P6、P7的加工过程；转子车间的子任务经过P8、P9、P10的加工过程；箱体车间的子任务经过P11、P12、P13的加工过程；总装车间的子任务经过P14、P15、P16、P17、P18的加工过程。当考虑同一时间窗口下多个订单的综合调度时，各订单子任务之间约束关系复杂，任何选择及调度偏差都将导致订单生产时间、生产成本及库存成本的变化，影响生产链效率。

调度模型的假设如下：

·在建立的模型中对于定制子任务，加工成本及加工时间固定且已知。由于所有调度方案的加工成本是相同的，所以在模型里不考虑加工成本。

·忽略企业之间的订货、运输时间及成本，仅考虑库存成本、加工时间、订单延迟损失与订单的优先级别。

·MC生产商的生产目标是，在尽可能满足各订单交货时间约束的条件下，尽量满足优先级顺序，之后尽早完成全部订单任务，并降低生产及在制品库存成本。

·当交货周期≤生产周期时，生产商需要大于正常生产能力才能完成交货，此时可能产生拖期交货现象，产生缺货成本。αi表示为定制产品i拖期生产单位时间内的惩罚因子；βi表示没有满足定制品i的单位时间内的惩罚因子[2]。

设MC生产商在时间域值T内接到M个订单，每个订单都可以分解为Ni（i=1,2,…,M）个子任务，每个订单的最迟交货期为的Di（i=1,2,…,M）。

为便于描述进行如下定义：

定义1：矩阵Ci为一个结构矩阵，是描述订单i各子任务可选方案参数的集合：

则MC的生产调度优化模型为：

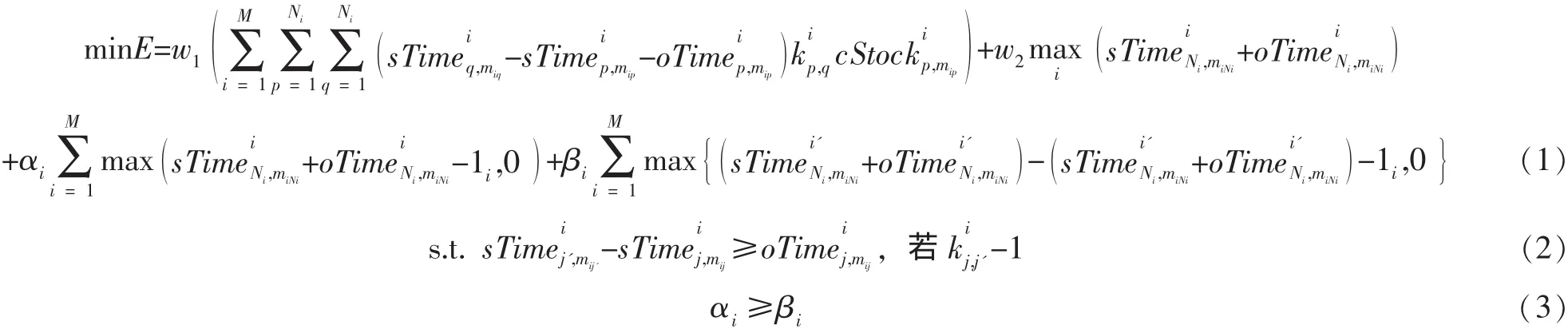
调度模型 （公式1）中的第一部分为库存成本评价因子；第二部分为时间评价因子；第三部分为订单延期惩罚项，第四部分为优先权惩罚因子。公式 （2）为同一订单各子任务之间的时间约束；公式 （3）表示延期惩罚远大于优先权惩罚约束。

2 基于粒子群算法的生产计划调度模型求解

2.1 粒子群优化算法概述

粒子群优化算法 （Particle Swarm Optimization，PSO）最早是由1995年由Eberhart和Kennedy共同提出的，其基本思想是受他们早期对许多鸟类的群体行为进行建模与仿真研究结果的启发[4]。算法模拟鸟群飞行觅食的行为,通过鸟之间的集体协作使群体达到最优。与遗传算法类似，它也是基于群体迭代，但没有交叉、变异算子，群体在解空间中追随最优粒子进行搜索。其数学描述如下：设zi=（zi1,zi1,…,ziD）为第i个粒子 （i=1,2,…,m ）的D维位置矢量，根据具体研究背景下事先设定的适应函数计算zi的适应值，以此来衡量粒子位置的优劣。在每次迭代中，粒子根据以下式子更新速度和位置：

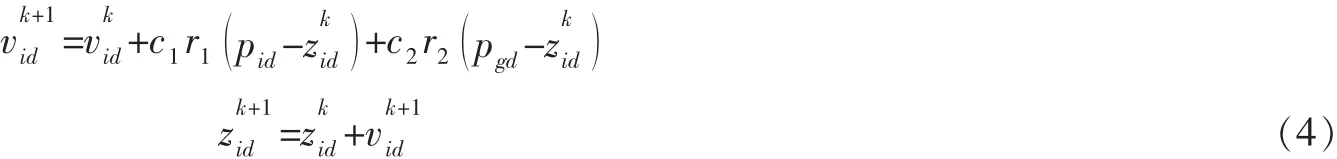
（4）式中的第1式的第二部分是 “认知”部分，代表了粒子的自身学习能力。第三部分是 “社会”部分，代表着粒子间的协作。两个式子表示粒子根据以上此迭代的速度、当前位置和自身最好经验与群体最好经验之间的距离来更新速度，然后粒子飞向新的位置[5]。

PSO的优势在于算法简单有效，容易实现，没有很多参数需要调整，且不需要梯度信息、收敛快等。PSO是非线性连续优化问题、组合优化问题和混合整数非线性优化问题的有效优化工具，因此本文同一时间窗口的调度优化采用粒子群算法来求解。

2.2 相关定义

为便于MC供应链下同一时间窗口订单优化调度问题的粒子群算法求解，通过以下定义将生产调度优化模型映射到图中。

定义2：图G为表示MC供应链动态调度问题的有向图，G（ N,A）。

定义3：虚拟起始点sPoint为不占用任何操作时间的节点，是所有粒子的出发点。由sPoint出发的弧指向图中所有对应规则库中无前置任务的节点。

2.3 算法描述

模型映射到图中后，即可运用类似TSP的搜索方法对问题进行求解。以下是具体算法步骤：

步骤1：初始化各参数。

步骤1.1：确定种群规模。

步骤1.2：确定学习因子c1和c2，初始代数k=0。

步骤1.3：初始化粒子的速度和位置，Vi（0）， Xi（0），同时定义速度和方向两个维度。随机产生第一代例子，即随机生成第一代粒子的遍历结果。

步骤2：构造遍历规则。运用JESS专家系统定义每个工序的前置工序，建立基本的遍历规则。调用JESS专家系统，根据已访问的节点和规则库中的访问规则，生成粒子可访问的节点集合。如果粒子的可访问节点集合为空，则说明粒子完成遍历。在数组中记录粒子的遍历结果。每个工序都有其前置工序，虽然粒子在遍历时存在一定的随机性，但是一定要符合流程规则。

步骤3：计算粒子的适应值。

步骤3.1：在粒子完成遍历后，采用顺推的方法确定找出各个子任务的最早开工时间和各个订单的最早完工时间。对于任何一个新取出的子任务j，通过JESS查询它的前置任务，取其前置任务完工时间的最大值trMax；查找遍历排序在它之前的最后一个相同子任务 （其它订单）完工时间rrSam。取max（ trMax,rrSam,0）作为子任务j的开工时间，并计算其完工时间。

步骤3.2：根据遍历顺序，从数组中读出各个节点相对应的成本。

步骤3.3：粒子完成一条路径的遍历，并计算出各节点的完工时间后，根据其遍历的各个节点，将各参数代入（1）公式计算其适应值。

步骤4：根据各个粒子的适应值找出局部最优pbest和全局最优gbest。由于学因子的存在，根据新速度的方向更新，粒子群体会向最优位置飞翔。

步骤5：更新速度和位置。产生新一代的粒子。

步骤5.1：粒子根据以下公式更新速度和位置。

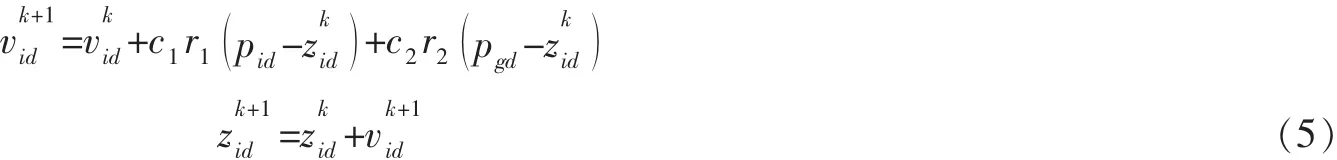
步骤5.2：根据新的适应值，如果优于原来的pbest和gbest，则替换为pbest（k）， gbest（k）。对于子群内所有个体均为不可行的解，或有多个个体同为最优解时，随机取其中一个为子群的当前最优解。

步骤6：判断粒子是否到达最大迭代数，是则退出循环，输出结果；否则，转入下一步。

步骤7：回到步骤2。

粒子群求解算法流程如图3和4所示。

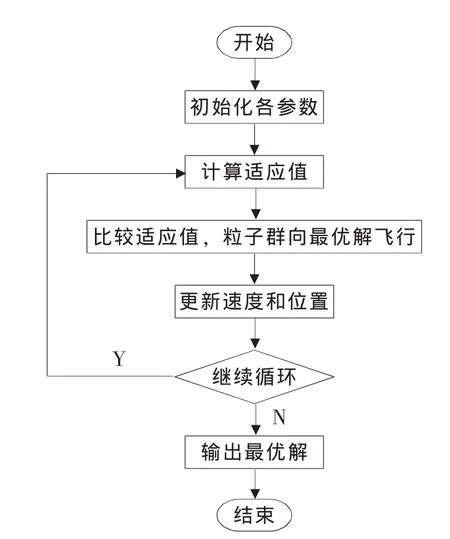
图3 主程序图

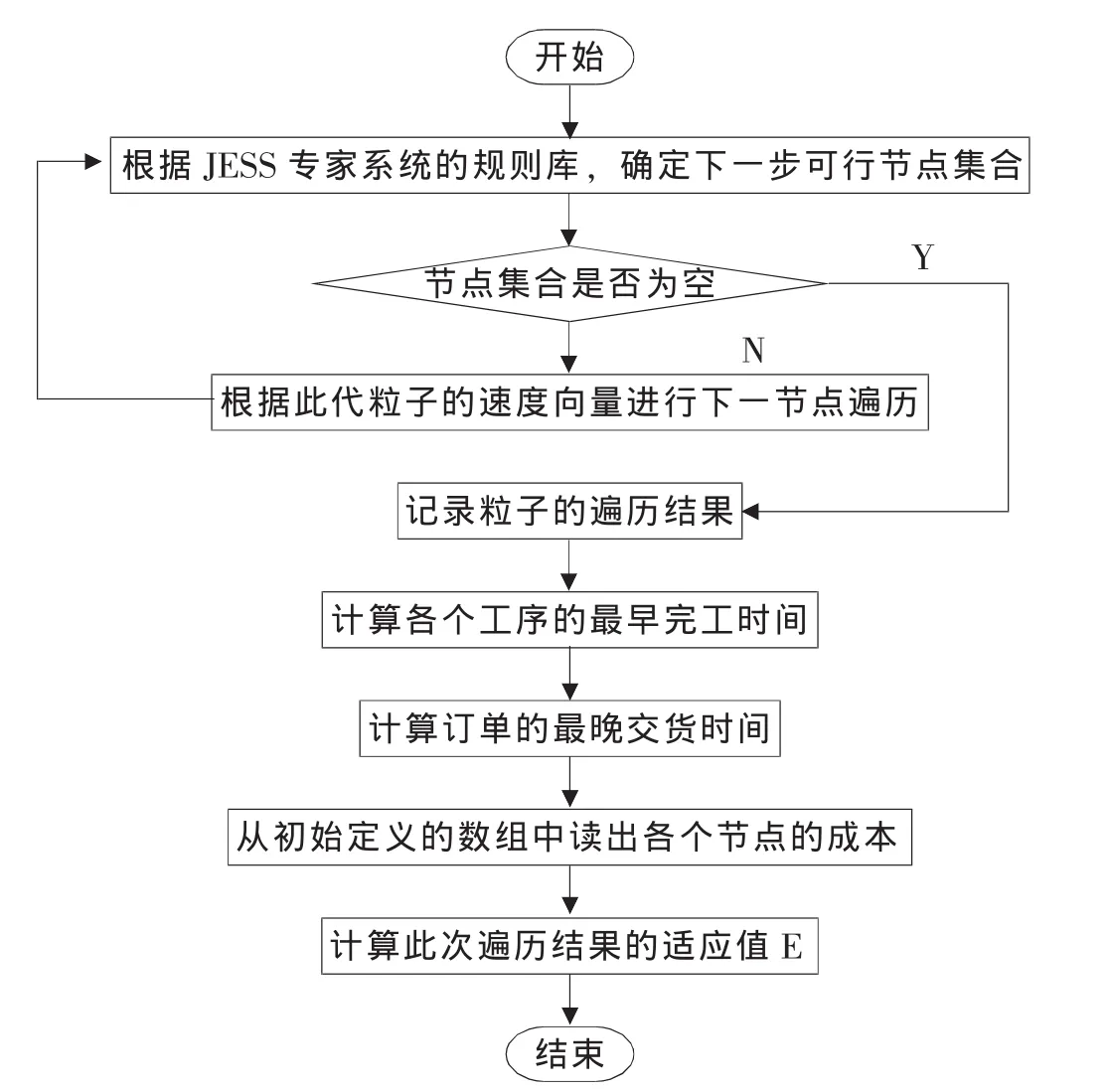
图4 粒子遍历程序图

3 仿真算例与结果分析

这里的算例，继续采用广州某MC机械厂的汽轮机生产的例子来说明。为了简化计算过程，便于调度结果优劣分析，这里抽取该机械厂汽轮机某一段定制生产过程数据，选择其中6个订单数据进行验证分析。这6个订单具有相同的订单分解结构 （如图2所示），表1为订单子任务在各企业内的处理时间；表2为生产能力表；表3为订单的生产成本，每单位时间的库存成本以在制品生产成本的0.5%计；表4为订单的最迟交货期和定制优先权。

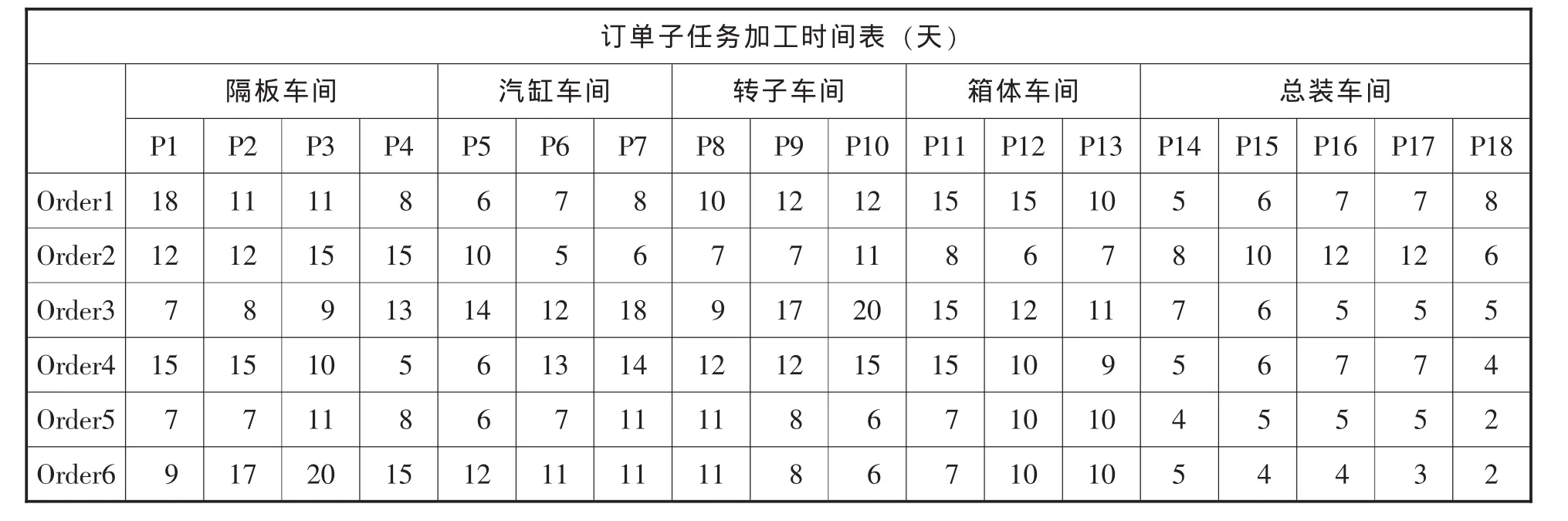
表1 订单任务加工表

表2 生产能力表

算例为6个订单，每个订单需要18个加工来完成，因此，每个订单各有18个子任务，不同子任务对应不同的加工点，即子任务j对应加工点j（ 0＜j＜=18），每个子任务对应的加工时间如下 （T_matrix ij代表加工第i个订单的第j个子任务的加工时间）：

表3 生产成本表

表4 交货期与定制优先权表

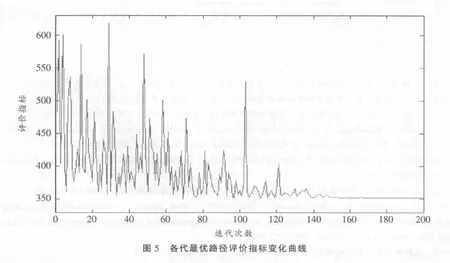
采用 [2.3]描述的算法，选取w1=0.015,w2=0.985,c1=2,c2=0.5,α=5,β=0.02得出最终的适应值为E=351.74。图5所示为某次调度优化过程中前200代的各代最优路径变化曲线。横坐标是迭代次数，纵坐标是目标函数数值。适应值在154代内的最优解为351.74，此时，库存的成本为2355.01（百元），完成订单任务共用时135天，6个订单共延迟33天，由于设置了对于延迟交货的惩罚因子α=5，所以在评价中，因延迟交货而产生的成本为165。优先劝惩罚因子β为0.02，所以因优先权产生的成本为11.9。多次实验结果均收敛于135个时间单位。50次试验中46次收敛于137个时间单位，2次收敛于134个时间单位，2次收敛于136个时间单位。

该算例的优化调度方案如图6所示。横坐标代表加工时间，纵坐标代表18个加工点，矩形框Pij（0＜i＜=6,0＜j＜=18）代表第i个订单的第j个子任务，如编号为P513则代表第5个订单的第13个子任务，矩形的长度则代表了子任务加工时间。如甘特图的左下角矩形P31，它的含义为：第3个订单的第1个子任务在加工点1上进行加工，为7个单位加工时间。

4 结 论

大规模定制是综合提升客户个性化需求与企业生产或服务效率的有效生产模式，是21世纪的主流生产模式，其生产与调度是实现企业大规模定制能力相当重要的一环，基于定制点分离思想，结合大规模定制生产的应用实践，本文构建了大规模定制同一时间窗口的订单优化调度模型，并以汽轮机生产的算例对模型进行了验证。对今后进一步研究大规模定制生产调度问题的提供了一定的帮助，对企业实施大规模定制的可行性研究也有一定的借鉴意义。

[1]季建华，赵平，顾巧论.基于大规模定制的流程工业生产计划优化方法及应用研究[J].信息与控制，2008,37(6)：362-365.

[2]孙靖，林杰.基于蚁群算法的大规模定制供应链调度优化研究[J].计算机应用，2006,26(11)：2631-2634.

[3]孙靖，林杰.信息不完全共享下MC供应链动态调度模型研究[J].系统仿真学报，2007,19(9)：1943-1949.

[4]J Jerald,P Asokan,G Prabaharan,et al.Scheduling optimization of flexible manufacturing systems using particle swarm optimizational gorithm[J].International Journal of Advanced Manufacturing Technology,2005,25(9)：964-971.

[5]F van den Bergh,A P Engelbrecht.A study of particle swarm optimization particle trajectories[J].Information Sciences,2006,176(8)：937-971.

[6]王玉，林杰，潘建玲.MC下基于多CODP的生产调度体系及其仿真研究[J].管理科学，2008,21(4)：17-25.

[7]WANG Yu,LIN Jie.Supply Chain Model Based on Multi-CODP in Mass Dynamic Customization[C]//Proceedings of the International Conference on Information Management,Innovation Management and Industrial Engineering.Los Alamitos：Inst.of Elec.and Elec.Eng.Computer Society,2008：252-255.

[8]王玉，林杰.大规模动态定制系统研究[J].计算机工程与应用，2010,46(5)152-155.

[9]WANG Yu.Supply chain optimization system of mass customization based on multi-CODP[C]//2009 Chinese Conference of Control and Decision.Singapore：IEEE Industrial Electronics,2009：3452-3457.

[10]王玉.大规模定制中客户订单解耦点定位的专家系统[J].计算机集成制造系统，2011,17(5)：924-934.