抛物线与特殊四边形存在问题探求
2012-08-28江苏省南通市通州区三余中学朱维东
☉江苏省南通市通州区三余中学 朱维东
抛物线与四边形作为代数和几何中最重要的章节,历来都是中考的必争之地,其中抛物线与特殊四边形存在探求问题更是将数形结合的数学思想体现得淋漓尽致,现将此类近年中考的常见题型加以归类,剖析解法,供读者参考.
一、抛物线与平行四边形存在问题
例1 (2011年凉山州)如图1,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1 (1)求抛物线的解析式; (2)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点F的坐标,若不存在,请说明理由. 图1图2 分析:(2)探究A、D、E、F为顶点的平行四边形,此类题目最常见,要注意分类讨论,分为AF为平行四边形的边和对角线两种情况. 解:(1)因为x2-4x-12=0, 所以x1=-2,x2=6. 所以A(-2,0),B(6,0). 又因为抛物线过点A、B、C, 故设抛物线的解析式为y=a(x+2)(x-6). 所以当x=4时,k=-4, 所以点D的坐标是(4,-4). 因为D(4,-4),所以E(0,-4),DE=4. 所以F1(-6,0),F2(2,0). 如图3,当AF为平行四边形的对角线时, 图3 所以E′的坐标为(n-6,4). (1)请直接写出抛物线c2的表达式. (2)现将抛物线c1向左平移m个单位长度,平移后得的新抛物线的顶点为M,与x轴的交点从左到右依次为A,B;将抛物线c2向右也平移m个单位长度,平移后得到的新抛物线的顶点为N,与x轴交点从左到右依次为D,E. 在平移过程中,是否存在以点A,N,E,M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由. 图4 分析:(2)在平移过程中,四边形ANEM始终满足对角线互相平分,首先肯定是平行四边形.要使它为矩形,只需满足对角线相等,即OM=OA. (2)存在,平移后得到的新抛物线如图5或如图6所示 图5图6 即M,N关于原点O对称,所以OM=ON. 因为A(-1-m,0),E(1+m,0), 所以A,E关于原点O对称,所以OA=OE, 所以四边形ANEM为平行四边形.要使平行四边形ANEM为矩形,只需满足,所以m=1. 所以当m=1时,以点A,N,E,M为顶点的四边形是矩形. 图7 (1)求直线AB的函数关系式; (2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由. 分析:(2)判断四边形为平行四边形的常用方法有四种,本题已经满足BC∥MN,故只要BC=MN时,四边形BCMN即为平行四边形;而判断平行四边形为菱形的常用方法有两种,本题是通过判断邻边是否相等来解决的. 设直线AB的解析式为y=kx+b,代入A、B的坐标,得 (2)在四边形BCMN中,因为BC∥MN, 所以当BC=MN时,四边形BCMN即为平行四边形. 即当t=1或2时,四边形BCMN为平行四边形. 此时BC≠CM,平行四边形BCMN不是菱形; 所以,当t=1时,平行四边形BCMN为菱形. 例4 (2009内蒙古鄂尔多斯市)已知t1,t2是方程t2+2t-24=0的两个实数根,且t1<t2,抛物线的图像经过点A(t1,0),B(0,t2). 图8 (1)求这个抛物线的解析式; (2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求▱OPAQ的面积S与x之间的函数关系式,并写出自变量x的取值范围; (3)在(2)的条件下,当▱OPAQ的面积为24时,是否存在这样的点P,使▱OPAQ为正方形?若存在,求出P点的坐标;若不存在,说明理由. 分析:(3)要使平行四边形OPAQ为正方形,只需满足对角线垂直且相等,此时可求出点P的坐标为(-3,-3),然后再验证该点是否在抛物线 因为抛物线与x轴的交点坐标为(-6,0),(-1,0). 所以x的取值范围为-6 代入解析式得:y1=-4,y2=-4. 所以点P的坐标为(-3,-4),(-4,-4). 当点P为(-3,-4)时,满足PO=PA,此时,平行四边形OPAQ是菱形. 当点P为(-4,-4)时,不满足PO=PA,此时,平行四边形OPAQ不是菱形. 而要使平行四边形OPAQ为正方形,那么,一定有OA⊥PQ,AO=PQ,此时,点P的坐标为(-3,-3),而(-3,-3)不在抛物线y=上,故不存在这样的点P,使四边形OPAQ为正方形.

二、抛物线与矩形存在问题



三、抛物线与菱形存在问题



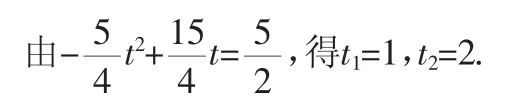
四、抛物线与正方形存在问题