关于课本一道分式方程练习的思考
2012-08-28广东省惠州市铁路学校
☉广东省惠州市铁路学校 陆 钢
义务教育课程标准实验教科书人教版八年级(下)P32题2解方程求x:

一、分式方程增根的产生原因与检验方法
通常分式方程是通过“在方程两边同乘各分母的最简公分母”去掉分母转化为一个整式方程(这里实际是一个一元一次方程)来求解,在这个去分母的过程中,未知数原来在分式中的取值有限制(不能使分母的值为零),到了整式中它的取值就不再受限制了,这样就产生了所求出的整式方程的解未必恰好是分式方程的解的问题,这就是增根产生的根本原因.所以解分式方程最后都需要检验,这里的检验并不是判断解题过程是否正确,而是要判断所求的解是否符合要求.
在解分式方程时,当我们确信自己的求解过程没有问题时,我们并不需要代入原方程的左、右两边去检验(可能更麻烦),我们只要代入最简公分母(若代入后求出的值恰好为零,说明这个解会使原分式方程的某个分母为零,这样方程中的那个分式就没有意义,这个解就是增根,要舍去;若代入最简公分母后,所求的值不为零,说明这个解能保证方程中各分式有意义,且使方程左、右两边的值相等,这个数才是分式方程真正的解).
二、分式方程解的情况探讨
任何一个一元一次方程,通过去分母、去括号、移项、合并同类项等变形手段都可以化为ax=b的形式.显然x的值是由a、b来确定的.当系数a≠0时,x有唯一值(即方程只有一个解x=;当系数a=0时,又分两种情况:1.若b=0,即0x=0,则x可取任何实数(即方程有无数多个解);2.若b≠0,即0x=b,此时x无解.
对于含字母系数的分式方程,若去分母后转化的是一元一次方程,它们解的关系为:1.若这个一元一次方程无解,则分式方程也无解;2.若一元一次方程只有一个解,则要进一步判断这个解会不会使分式方程的分母为零,若使分母为零,则是增根,舍去,这样分式方程无解了;若不会使分母为零,它就是分式方程的根,此时分式方程只一个解;3.若一元一次方程有无数个解,则分式方程也有无数个解(需说明的是这无数个解中必然存在使分式方程的分母等于零的数,也就是分式方程的增根,应排除).
三、问题的提出
课本两道分式方程中的系数都含有字母,并且题后附加了一定的条件,大多数学生在解这两个方程时,对条件不知道怎么用,甚至假装“视而不见”.究其深层原因是对分式方程的解缺乏深刻理解,表层原因是只习惯于模仿性的解题,不会主动分析数量关系,缺乏理解、思考的意识与能力.事实上,不仅是学生,就是许多老师解这种题型也常常丢三落四,漏洞百出.现在我们去掉题后附加条件来探讨一下这两道方程的解的情况:
1.当b-1=0时(即b=1时):
(1)若ab-2a=0(即a=0时),则对于方程②来说x可取任意实数,即当b=1且a=0时,方程②有无数个解(含x=0),但对于方程①来说,x=0是增根,应舍去.即在b=1且a=0的条件下,方程①的解为除0外的任意实数.
(2)若ab-2a≠0(即a≠0)时,方程②无解,这样方程①也无解.
1.当n-m=0时:
(1)若m=0(n=m=0时),方程④有无数个解(含x=0,x=-1,而这两个对于方程③来说是增根,应舍去),所以当n=m=0时,方程③的解为除0和-1外的任意实数;
(2)若m≠0(即n=m≠0时),方程④无解,则方程③也无解.
从以上两题的解题过程可看出,保证题1有唯一解的条件是b≠1且a≠0;保证题2有唯一解的条件是n≠m且mn≠0.然而课本在题1所附条件中就缺少了条件a≠0.
四、问题的思考
不少同学惧怕几何题的推理论证,因为几何证明技巧性强,变通性差,事实上代数推理比几何推理更难掌握,更可以考查一个人的智力水平,代数题的解法通常多种多样,只要有理,殊途同归.学生之所以认为难,跟这方面题型“出镜率”低,练得少有一定的关系,另外跟一些老师本身的专业素质也有关,有些老师遇到此类问题时,常常回避不讲或讲不清楚,学生当然就更难学好了.教师面对类似问题不应该回避,应该注意通性通法,把道理讲清楚,原理讲透彻.原理性的东西学生掌握了,就可以以不变应万变,触类旁通,举一反三.
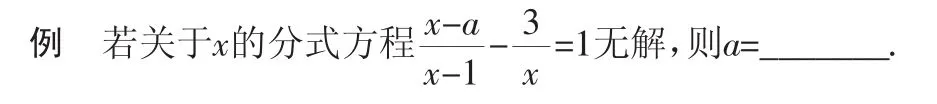
分式方程无解有两种情况:(1)是去分母后所得整式方程无解;(2)是所得整式方程的解使分式的分母为零,即解为增根).只有学生理解了分式方程无解的道理才可能得到准确答案(a=-2或1),否则就会漏掉答案-2.
数学知识其实并不多,知识原理弄懂了,“放之四海而皆准”,很多头脑聪明灵活的学生为什么偏爱数学,一个重要原因就是数学要记要背的东西少,花的时间少,学得轻松,容易找到成就感.作为老师,提高数学专业素养,任重而道远.
