有心插柳柳成荫——例谈三角形内角和的一种变式推广和应用

☉江苏省淮阴中学新城校区 赵惠敏 吴从洋

有心插柳柳成荫
——例谈三角形内角和的一种变式推广和应用

☉江苏省淮阴中学新城校区 赵惠敏 吴从洋

七年级数学学习中，学生正式接触到以图形语言、符号语言形式呈现的图形问题，在教学中，一些看似简单的几何图形，如果对它深入研究，充分挖掘，会收到意想不到的收获，这类题一般都具有典型性、示范性和迁移性，因此具有较高的应用价值.针对这些问题，在教学中尽量采取：定位基础图形，突出知识点间的联系，鼓励学生运用所学知识，多方位、多角度的思考和解决问题，有助于学生思维的求新求变，下面以一道题为例，作一介绍.

原型 如图1，AC、BD相交于点O，则∠6+∠5和∠3+∠4相等吗？为什么？

分析：由三角形内角和等于180°，可以得到∠6+∠5+∠1=∠3+∠4+∠2=180°.又由图形条件知，对顶角∠1、∠2相等，因此，∠6+∠5=∠3+∠4.

假如AB∥CD，上述方法仍然适用，还可以由AB∥CD得到∠6=∠3，∠5=∠4，从而∠6+∠5=∠3+∠4.这是七年级常见的一道几何题.也就是说无论AB、CD是否平行，都可以得到∠6+∠5=∠3+∠4.

我们将这种类似的图形称为“8”字形，由上面的推理可以得到：“8”字形中除对顶角外的两个相对的内角和相等.表面看这道题似乎很平常，实际上这个结论在许多题型中有着广泛的应用.

图1

一、在求多边形的内角和中的应用

苏科版七年级下册，学生学习到了三角形内角和、外角和、多边形内角和及外角和等知识，经常会有一些复杂的图形要求计算内角和的问题，下面笔者例举几种常见的复杂图形，添加辅助线，构造“8”字形，可以迅速解题.

例1 如图2，试求出∠A+∠B+∠C+∠D+∠E+∠F的和.

图2

分析：对于复杂及不规则图形问题，教师通常应引导学生添加辅助线构成规则图形，以利于求解，此题有多种解法：如构造五角星，两次运用三角形的外角定理等.笔者主要介绍如何构造“8”字形.联想到“8”字形中两个三角形相对两个内角的和相等，利用这个结论添加辅助线，连接AF，可知∠B+∠D=∠FAD+∠AFB，这样将6个内角的和转化为四边形AFEC的4个内角的和，进而得到结果为360°，而且这种添加辅助线的方法有三种连接方法，连接BC或ED都可以，解题原理不变.还有类似的典型题目，比如：

在图3中，猜想：∠A1+∠B1+∠C1+∠A2+∠B2+∠C2等于多少？请说明你的理由.

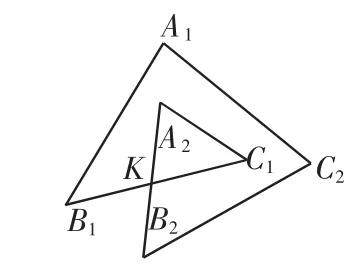
图3

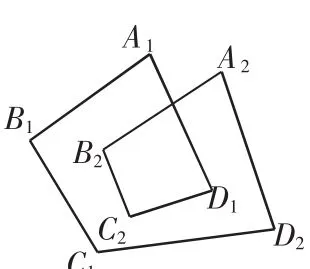
图4

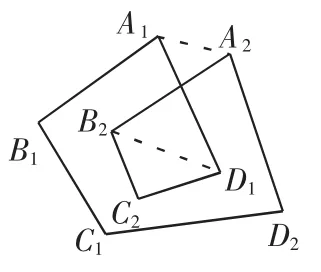
图5

如果把图3称为2环三角形，图4称为2环四边形，它的内角和∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2等于多少？

分析：类似于例1，在图3中连接B1B2，转化为四边形，内角和为360°，在图4中连接A1A2，B2D1（如图5），转化为一个五边形和一个三角形，内角和为720°.此题还可以推广到2环n边形（如图6），它的内角和为360°（n-2）.

评注：学生在解题过程中充分联系了平时教学知识点中的结论，虽然这些结论不能用于直接说理，但是为问题的解决找到了很好的突破口，对学生解题信心的确立是很有帮助的.教学中，某些特殊或重要的知识点及结论，要让学生做到熟记并灵活运用，这类变式问题是不错的选择，既避免了简单重复的枯燥，也增强了学生解题的趣味和斗志.

图6

二、在说理题中的应用

例2 如图7，已知线段AB、CD相交于点O，连接AD、CB，我们把形如图7的图形称之为“8”字形，如图8，在图7的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N.

（1）在图7中，请直接写出∠A、∠B、∠C、∠D之间的数量关系.

（2）在图8中，试问∠P与∠D、∠B之间存在着怎样的数量关系（直接写出结论即可）.

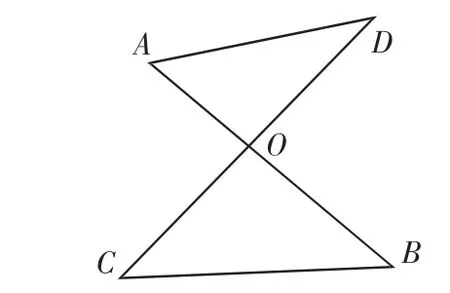
图7

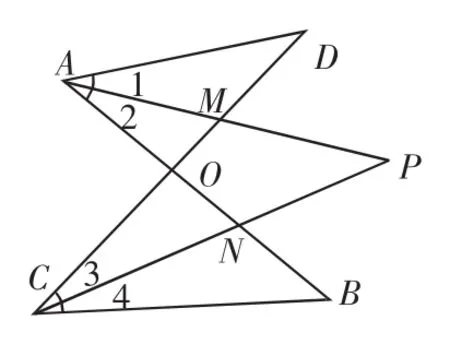
图8

分析：（1）∠A+∠D=∠B+∠C；（2）∠D+∠B=2∠P.

图8存在两个“8”字形，所以相等的内角和有两对，分别是：∠1+∠D=∠3+∠P，∠4+∠B=∠2+∠P. 由于AP和CP分别平分∠DAB和∠BCD，所以∠1=∠2、∠3=∠4，根据等式性质，将上面等式相加，消去相等的量得∠D+∠B=2∠P.

在七年级的学习中还会遇到求线段之间关系等一类问题，学生通常只会求出线段的相等关系，而忽视了线段的位置关系，对于这类题目，学生如果熟悉“8”字形的结论，那么会很容易得到线段的位置关系.

例3 如图9，两个不全等的等腰直角三角形OAB和OCD叠放在一起，并且有公共的直角顶点O．

（1）AC、BD有什么样的关系？

（2）将图9中的△OAB绕点O顺时针旋转一个锐角，得到图10，这时（1）中的两个结论是否成立？

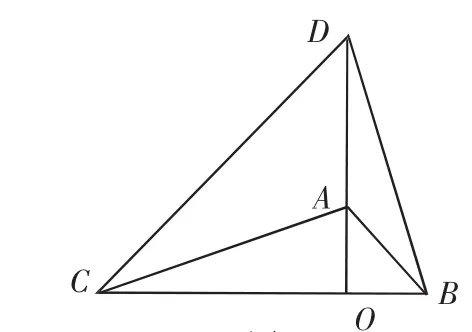
图9

图10

分析：（1）如图11，因为△OAB和△OCD都是等腰直角三角形，且叠放在一起，所以OA=OB，OC=OD，且∠COD=∠AOB=90°.所以△COA S△DOB，所以AC=BD，∠1=∠2.如果延长CA，交DB于E，就构成了一个“8”字形，从而利用“8”字形的结论，∠1+∠4+∠DEC=∠2+∠3+∠COA=180°. 又∠4=∠3，即可得∠DEC=∠COA=90°.

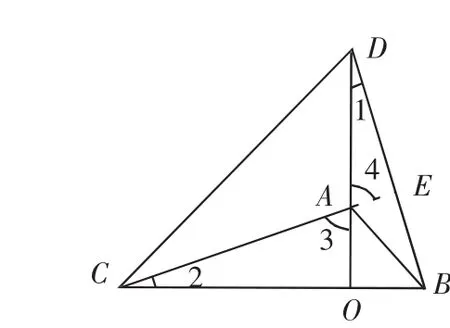
图11

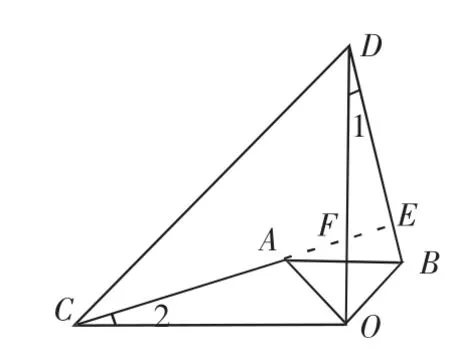
图12

（2）和（1）类似（如图12），先证△COA S△DOB，如果延长CA，利用“8”字形的结论，即可得∠DEC=∠COA=90°，实际上，若△OAB绕点O继续旋转更大的角（大于0小于180°），结论仍然成立.

评注：复杂图形中基本图形的挖掘是解决图形问题的关键，学生思想中基本图形的形成，死记硬背、生搬硬套是没用的，而要以理解替代，让学生在完成学习任务的同时享受到成功的喜悦和学习数学的乐趣.

由上述几例可以看出：许多几何问题，初看似乎无从下手，难于思考，但是如果认真寻找与之接近的熟悉题目，从题目的相通或相同点切入，好好想一想与自己形成的基本图形知识存在的联系，充分利用基本图形的结论，解题思路便会豁然开朗，难题也“活”了，当然并不是所有的几何问题都能利用基本图形得到很好的解决，但只要我们在解题时，善于抓住问题的特点，充分利用基本图形分析问题，运用基本图形对几何解题的启示和简化功能总会出奇制胜.对于这些基本图形，我们要想达到“见到图形，想到性质，想全性质”，就必须把它们拿出来认认真真加以研究，形成基本图形储备起来.在头脑中形成系统完备的待用基本图形库，最终把基本图形当做利刃，用到解题中去.在本文中，笔者从一道最基本的题型出发，“有心插柳”，充分挖掘，探索得到“8”字型的结论，从而利用结论去解决一类复杂图形的问题，达到“柳树成荫”的效果！

总之，只要我们教师对基本图形的深入学习和研究，我们的学生在运用基本图形解决几何问题的能力，一定能提高到一个崭新的水平.