浅析来自生活中的一次函数问题
2012-08-28河南省淮阳第一高级中学王寸真
☉河南省淮阳第一高级中学 王寸真
浅析来自生活中的一次函数问题
☉河南省淮阳第一高级中学 王寸真
一元一次函数在我们的日常生活中应用十分广泛,当人们在社会生活中从事买卖特别是消费活动时,若其中涉及变量的线性依存关系,则可利用一元一次函数解决问题.例如,当我们购物、租用车辆、入住旅馆时,经营者为达到宣传、促销或其他目的,往往会为我们提供两种或多种付款方案或优惠办法.这时我们应三思而后行,深入发掘自己的数学知识,做出明智的选择.可以利用一次函数来指导购物,既锻炼了数学头脑、发散了思维,又节省了钱财、杜绝了浪费,真是一举两得啊!利用一次函数关系式,同学们可以解决很多生活中的实际问题,举例说明如下.
一、依法纳税问题
例1 依法纳税是每个公民应尽的义务.从2008年3月1日起,新修改后的《中华人民共和国个人所得税法》规定,公民每月收入不超过2000元,不需交税;超过2000元的部分为全月应纳税所得额,都应纳税,且根据超过部分的多少按不同的税率纳税,详细的税率如下表:
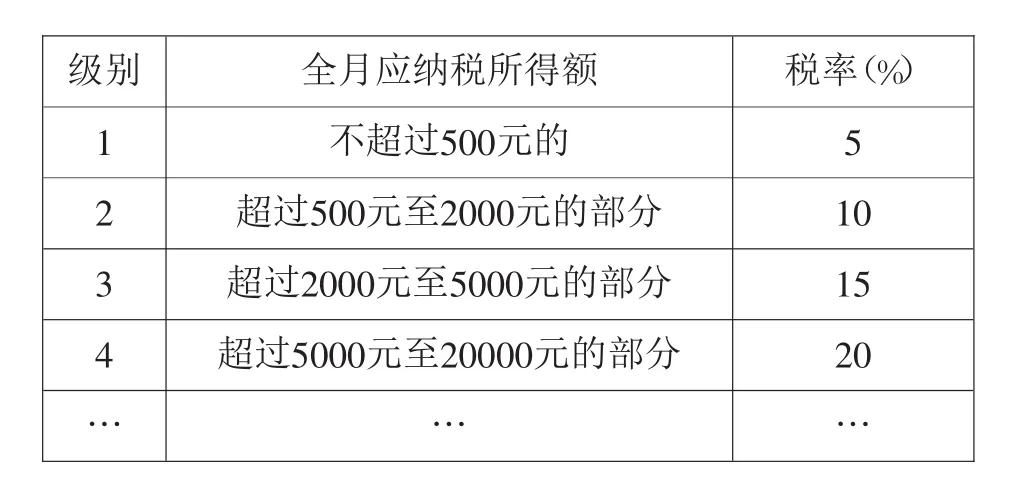
级别 全月应纳税所得额 税率(%)1不超过500元的 5 2 超过500元至2000元的部分 10 3 超过2000元至5000元的部分 15 4 超过5000元至20000元的部分 20………
(1)某工厂一名工人2008年3月的收入为2400元,问他应交税款多少元.
(2)设x表示公民每月收入(单位:元),y表示应交税款(单位:元),当2500≤x≤4000时,请写出y关于x的函数关系式.
(3)某公司一名职员2008年4月应交税款120元,问该月他的收入是多少元.
解:(1)该工人3月的收入2400元中,应纳税的部分是400元,按纳税的税率表,他应交纳税款400×5%=20(元).
(2)当2500≤x≤4000时,其中2000元不用纳税,应纳税的部分在500元至2000元之间,其中500元按5%交纳,剩余部分按10%交纳,于是,有y=[(x-2000)-500]×10%+500×5%=(x-2500)×10%+25,即y关于x的函数关系式为y=(x-2500)×10%+25=0.1x-225(2500≤x≤4000).
(3)根据(2)可知,当收入为2500元至4000元之间时,纳税额在25元至175元之间,于是,由该职员纳税款120元,可知他的收入肯定在2500元至4000元之间.
设他的收入为z元,由(2)可得(z-2500)×10%+25=120,解得z=3450,故该职员2008年4月的收入为3450元.
评析:我国的税收是取之于民,用之于民,公民有纳税的义务,通过本题的考查,使学生进行了税收知识的教育.本题以修改后的新《个人所得税》规定为背景,通过建构分段函数的数学模型,对不同范围内的月工薪进行计算,得出有关数据.
二、抗震救灾问题
例2“5·12”汶川地震发生后,某天广安先后有两批自愿者救援队分别乘客车和出租车沿相同路线从广安赶往重灾区平武救援,图1表示其行驶过程中路程随时间的变化图像.
(1)根据图像,请分别写出客车和出租车行驶过程中路程与时间之间的函数关系式(不写出自变量的取值范围).
(2)求客车和出租车行驶的速度分别是多少.
(3)试求出出租车出发后多长时间赶上客车.
解:(1)客车行驶过程中路程与时间的函数关系式为y=40x;
出租车行驶过程中路程与时间的函数关系式为y=100(x-2).(2)客车行驶的速度为40千米/时,出租车行驶的速度为100千米/时.


图1
评析:行程问题是一个常规的问题,而新课标下的行程问题,与原来行程问题的应用题完全不同,往往与图像、图形、表格等结合在一起,不仅考查了学生的数学知识,而且考查了学生的识图能力和数形结合的数学思想.
三、调运方案问题
例3 抗震救灾中,某县粮食局为了保证库存粮食的安全,
坛决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表(表中“元/(吨·千米)”表示每吨粮食运送1千米所需人民币).
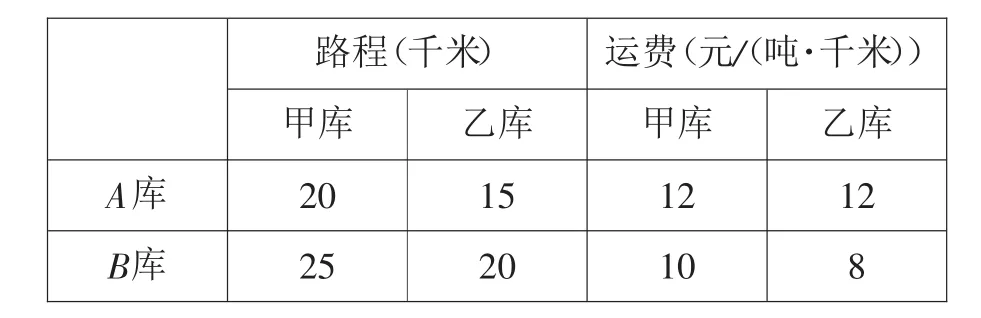
路程(千米)运费(元/(吨·千米))甲库 乙库 甲库 乙库A库 20 15 12 12 B库 25 20 10 8
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式.
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,这时总运费是多少?
解:(1)依题意有:


(2)上述一次函数中k=-30<0,
所以y随x的增大而减小.
所以当x=70吨时,总运费最省.
最省时的总运费为-30×70+39200=37100(元).
答:从甲库运往A库70吨粮食,往B库运送30吨粮食,从乙库运往B库80吨粮食时,总运费最省为37100元.
评析:最优化问题是生活中常遇到的问题,人们要对各种方案有所选择和决策.上述问题是通过构建一次函数的数学模型的方法,利用一次函数的增减性,求出函数最大值或最小值,最后从数据中得出最优化方案.
学生最感兴趣的是用函数知识解决发生在身边的实例,一次函数是一种重要的函数,运用一次函数可以解决日常生产、生活中的实际问题.我们要灵活运用所学知识来解决实际问题,特别要有把实际问题通过建立函数模型的能力和运用数形结合的思想来解决的意识.
