『点评者』的情怀——例谈数学教师的点评艺术

☉江苏省海安县李堡镇初级中学

☉江苏省南通市中青年名师工作室符永平工作室 刘东升

『点评者』的情怀
——例谈数学教师的点评艺术

☉江苏省海安县李堡镇初级中学

☉江苏省南通市中青年名师工作室符永平工作室 刘东升

*本文为“中学数学‘再创造’发现式系列课型研究”课题研究成果之一，该课题系江苏省“333高层次人才培养工程”196项科研资助项目（2010年10月由江苏省人才工作办公室公布，全省基础教育共2项）之一，项目编号为ВrА2010046，主持人：符永平．本文作者刘东升为课题组核心组成员．

《义务教育数学课程标准（2011年版）》关于“课程基本理念”下第3点即指出：“教学活动是师生积极参与、交往互动、共同发展的过程，有效的教学活动是学生学与教师教的统一，学生是学习的主体，教师是学习的组织者、引导者与合作者”［1］．笔者曾在文［2］中就教师作为组织者、引导者与合作者结合案例进行了一些个性化阐释．特别地，笔者在想，在学生“讲题”活动下，当学生讲解不到位或出错时，当师生对话走向深入时，当一些精彩的“课堂生成”（甚至“课堂意外”）出现后，教师的又一个重要身份——“点评者”出现了，这时“点评者”的情怀又显得十分重要．本文从最近几则教学案例出发，笔者给出关于“点评者”情怀的思考，与同行们分享．

一、案例展示

案例1

这是中考前一次模拟考试卷上一道填空题讲评片断，笔者所带班的科代表谭笑同学一次“错解展示”、师生的追问与对话．

题目 如图1，以BC为直径的⊙O与△ABC的另两边分别相交于点D、E．若∠A＝70°，BC＝2，则图1中阴影部分面积为________．

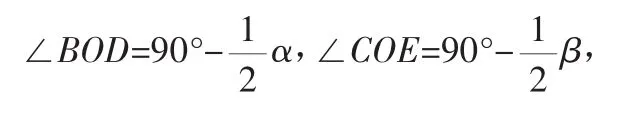
图1

师：对她的思路，大家有什么看法？

储伟煜：他的思路总体是对的，但答案错了，还没看出来错在哪儿？可能算错了吧！

师：你是怎么想的？

储伟煜：我也是这样思考的，但两个扇形的圆心角的和跟她不一样，我算的是140°.

师：说说你是如何算的.

储伟煜：我也是先算出α+β=110°，然后在△ABC和△COE中思考，这是两个等腰三角形，有∠BDO+∠CEO=α+β=110°，于是∠BOD+∠COE=360°－110°－110°=140°，进而我算出的答案是π．

师：这个数据是对的！大家看谭笑同学错在哪儿呢？

师：很好！现在我告诉大家，我在谭笑同学试卷上批阅意见：“记错‘经验’？这种跳步的风险很大，对于考试来说，宜从头开始慢慢演算．”

师：当然，现在我们再回头看看谭笑同学这道题目中很多可取之处：第一，她的求解方向和出发点是准确的；第二，她识别“模式”的努力是值得肯定的，尽管在本题中她记错“经验”，但她的这一经验对于已知等腰三角形顶角求底角是很有意义的！

（我看到谭笑同学一直尴尬的表情终于有些舒展，是因为我的点评中给予了她以“保护”吗？）

案例2

这是杜亚君同学在一次概率讲题出错后，师生对话与点评的真实记录，试看该生课后撰写的“反思小文章”．

一道概率问题的“讲题”历程

九年级（2）班 杜亚君

老师安排我讲解一道概率试题：

经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转．如果这两种可能性大小相同，三辆汽车经过这个十字路口，求下列事件中的概率．

（1）三辆车全部继续直行；

（2）两辆车向右转，一辆车向左转；

1.完善培养与引进人才的相关制度。人才供给是制约中西部等地区经济发展的一大问题，解决这个问题需要意识到留住人才最重要的是留住人才的心。企业可以从构建良好环境入手，建立薪酬激励和晋升制度，提高员工的工作积极性；提供完善的培训方案，为员工个人需要的满足和自我价值的实现提供条件。

（3）至少有两辆车向左转．

老师先让我上黑板做，首先我看到题目条件较复杂，应先简化．记三辆车为A、B、C，记直行、向左转、向右转分别为a、b、c，则可列树形图：

当我正忙于后续求解时，有同学在下面说：出错了！看了看老师，老师示意让我自己纠正．我似乎也意识到一种错误：我只认识到一面，还没有认识全面，但也想不出该怎么构造树形图．这时老师让另一个同学（科代表）上来帮助我，她将树形图重画了一下，如下：

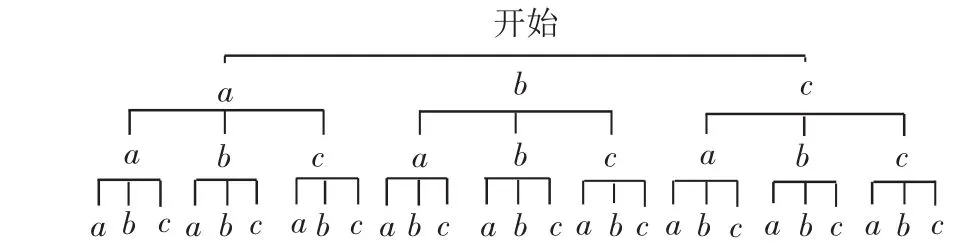
柳暗花明了！我也终于明白了她的意思，这个树形图才是符合题意的，答案也就顺利得到了：

刘老师小结了我们的解法，说：刚才杜亚君同学的错误解法在于树形图出错，可见，此类问题能否根据题意规划出准确的树形图是“破题”的关键．当然，我们要指出，虽然杜亚君同学的解法出错，但他上来就将问题中的文字信息选用相应的字母来代替的这种思想是值得肯定的，这是代数中的一种“符号化”意识，这样做往往能把繁杂的信息用简明的字母或符号表示出来，后来科代表的树形图沿用了他的字母，就体现了这种“符号化”的优势．

随感：从错误的解题过程中，老师帮助我找出合理的成分，让我有“面子”的回到座位，我进一步思考认为，要将概率问题全面思考，认真构造出符合要求的树形图，可使解题更严谨、缜密．数学是一个集严谨、全面于一身的学科，这道题的讲解经历让我受益非浅．

案例3

这是七年级吴宗泽同学在学“代入消元法”时，课堂板演中的一次错误与纠错的经历，课后该生在“反思小文章”中颇有感触地记录下来．

谢谢您，我的老师

——一次“代入消元法”的课堂板演经历

七年级（3）班 吴宗泽

学习二元一次方程组的解法时，我知道了二元一次方程组求解的关键是——消元，而消元法又有两种手段：第一种是代入消元法，第二种是加减消元法．这节课我们学的是第一种方法代入消元法．

当然正准备返回座位时，数学老师在这道题最后答案处打了一个红叉叉．

老师把我“留下了”，请同学们帮助订正．

我细看看，做得这么详细，还有什么问题呀？

师：错在哪儿呢？

同学2：他在算方程“－13x=－19.5”时出错！

师：是的．但大家要知道，吴宗泽同学对这道题就本节课所学的用代入消元法解二元一次方程组的方法来说，从他的解题过程来看，他是能得“满分”的，因为他的消元是成功的．他的出错是另一层面上的一元一次方程“系数化为1”时的粗心出错．顺便指出，对于二元一次方程组的解法，在成功消元后获得的一元一次方程，其解法步骤不必像上学期那样步步展示了，直接解出即可，刚才的例题示范中简明的步骤要注意体会．这也是同学们在做数学解答题时需要学会“省略非必要表达成份”．对了，小吴同学还忘了“结束语”呢，真是不该写的多写了，该写的还不全呀！

还好老师的这番“点评”让我“体面”地回到座位上，但这次经历给我两点感悟：

第一，课堂上不但要认真学习新的方法，还要严谨细致的运算和简洁的表达过程；

第二，这让我明白了一些道理：老师那道红叉叉画得很小，还有后来的那种点评，这是在保护我的自尊心吗？让我“体面”地回到座位上，这是一种情怀呀！这让我想起那篇《迷途笛音》中的卡廷先生……谢谢您，我的老师．

二、“点评者”的情怀

近读裴光亚先生《评课者的情怀》［3］，颇多感触．下面结合上述案例展开述说教师作为一个“点评者”的情怀．

1．“点评者”需要欣赏、维护与宽容

熟悉中小学课堂的同行都有这样的感受：小学生课堂氛围要好于中学，具体表现在积极举手发言，参与课堂交流与对话（很多小孩甚至喜欢抢答）；初中阶段，又是七年级好于八年级，到了九年级，课堂上积极参与发言、交流与质疑的就比较少了．这一方面与学生的心理成长特点有关，另一方面与长久以来我们教学里有一种“害怕”有关，特别地，这里简单提及美国教师雷夫·艾斯奎斯在《第56号教室的奇迹》中所记述的：“这年头，大多数的教室都被一种东西控制着，那就是‘害怕’．老师们害怕：怕丢脸、怕不受爱戴、怕说话没人听、怕场面失控．学生们更害怕：怕挨骂、怕被羞辱、怕在同学面前出丑、怕成绩不好、怕面对父母的盛怒．”［4］笔者以为，打破这种“害怕”的局面，首先在于作为一个“点评者”的教师，要有一种欣赏、维护与宽容的情怀，向学生传递一种认知：教室是一个可以出错的地方，重要的是我们对于错误的态度（如从纠错走向究错）．特别地，认真倾听、理解学生的表达和思维，并从中发现合理成分，引导学生欣赏，这本身又是一种对于学生的宽容与维护．如在上述案例1中，从谭笑同学开始很尴尬的表情舒展开来；从案例3中吴宗泽同学记述的“老师那道红叉叉画得很小”、“这让我想起那篇《迷途笛音》中的卡廷先生”……这既是对孩子们的大胆示错的一种肯定，同时一个为师者职业幸福不也油然而生吗？

2．“点评者”应该坚守价值引领

需要指出的是，笔者提倡教师作为“点评者”要有一以贯之的点评情怀，并不是混淆是非，颠倒黑白.恰恰相反，作为“点评者”，需要有鲜明的价值导向，以便引领学生明了对错、守住底线并“取法乎上”．如上文案例1中，笔者没有开始即肯定学生的思路方向正确、出发点准确等合理成分，而在于追问其他学生进行“纠错”，并再度追问实现了“究错”，最后点评时才给出了“错误中有合理成分”的评价，这一过程本身就是在坚守一种价值引领：先试着消除错误，获得问题的完整求解，再分析合理成分，指出努力方向；再有，案例2中，面对概率问题的关键所在——树状图的分析出错，旗帜鲜明的指出这一错误的严重性，进一步再指出该生其中的“合理性”：善于用符号表示，实现了问题的抽象和简化；而对于案例3中，该生的错误相对这一节新授内容来说，就不是严重的失误，只是一种低级的“笔误”，需要借此向所有学生传达的价值在于：代入消元的思路、步骤完全正确，同时要学会省略非表达成分．

3．“点评者”难在给出即时评价

面对课堂生成，作为“点评者”的教师要像一个节目主持人那样给一些“意外场景”出点评，但这种点评最大的难点在于“即时性”，即需要教者根据临时生成的一些观点、解法、表述等，进行准确的理解，进而迅速给予评价．如前所述，这种点评既要基于一种欣赏、维护和宽容的情怀，又要有鲜明的价值引领，可见，这种“即时性”的要求对教师的专业功底提出了很高的要求，也是数学教师一方面需要发挥的“特殊”的专业引领价值；另一方面，又要注意提高教师的交流、表达艺术．特别地，结合多年来学生“讲题”的实践，笔者关于这种“即时点评”提几点意见供参考：第一，尽可能精心“预设”，即课前要充分考虑学生可能有怎样的对话、“生成”，进而思考应对策略.第二，课堂上认真倾听学生的思路、尝试理解他们的思维特点，如果学生思维跳跃太大，通过追问促使其暴露、展开思维过程，以便后续点评时发现思维亮点或错误中的合理成分.第三，对于短时难于作出有效评价或引领的“生成”，可追问学生的理解与思考，为自己赢得更多的思考和深入的时间．这是针对一些同行，总喜欢急于表达自己的一时一刻的想法，但点评又不准确、不深入而言的.第四，对于一些精彩的生成，如果限于课堂上的时间或其他难于深入点评，可安排当事学生记下过程，课后教师参与讨论和点评“学生反思小文章”，将问题深入下去．特别地，笔者这一做法得到人民教育出版社中学数学室章建跃教授的鼓励：“让学生写反思性小论文，实际上就是把学习的过程完整化，加强学生对自己学习过程的自我监控和调节，使学生对知识的理解得到升华，获得更好的数学认知结构，同时在数学思想方法、解题策略等方面也得到系统化，效果肯定会好的．”

三、写在最后

本文本质上是指向“点评的艺术”，这是个老生常谈的话题．作为本文的结束，笔者想提醒一下同行们，在当下普遍提倡关注学生、关注学情的“取向”下，是不是应该也关注郑毓信教授在文［5］引述的关于数学教育理论研究的这样一个发展趋势：“……进而，如果说20世纪的最后20年称为‘学习者的时代’（the era of the learner），那么，在过去几年中我们就已进入到了‘教师的时代’（the era of the teacher），这也是指研究者们现在更多地聚焦于教师的教学行为．”

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）.北京：北京师范大学出版社，2012：1.

2.刘东升.学生“讲题”，教师应该“在场”——再谈学生“讲题”活动中的教师主导性.中学数学，2012（06）：56-58，60.

3.裴亚光.评课者的情怀.中学数学教学参考·中旬刊，2012（1-2）：3-6.

4.【美】雷夫·艾斯奎斯.第56号教师的奇迹.卞娜娜，译.北京：中国城市出版社，2009.

5.郑毓信.教师“实践性智慧的内容与发展途径”——兼论 “学科内容教学法知识”的实践性解读.中学数学月刊，2011（12）：1-4.