研题因反思而升华,编题因创新而精彩——2011年扬州市中考压轴题引发的思考
2012-08-28江苏省高邮市武安初中赵友忠
☉江苏省高邮市武安初中 赵友忠
研题因反思而升华,编题因创新而精彩
——2011年扬州市中考压轴题引发的思考
☉江苏省高邮市武安初中 赵友忠
“研题因反思而升华,编题因创新而精彩”,对于中考题的研究可以更好地弄清楚命题者的意图.在平时的教学中,我们一线教师要有意无意地对中考题进行深刻的研究.笔者在认真研读扬州市中考压轴题第28题之后,将自己的感受总结如下.
一、中考试题展示
(2011年扬州市中考题第28题)在△ABC中,∠BAC=90,AB<AC,M是BC边的中点,MN⊥BC交AC于点N.动点P从点B出发沿射线BA以每秒厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP.设运动时间为t秒(t>0).(1)△PBM与△QNM相似吗?以图1为例说明理由(.2)若∠ABC=60,AB=4厘米.①求动点Q的运动速度;②设△APQ的面积为S(平方厘米),求S与t的函数关系式;(3)探求BP2、PQ2、CQ2三者之间的数量关系,以图1为例说明理由.
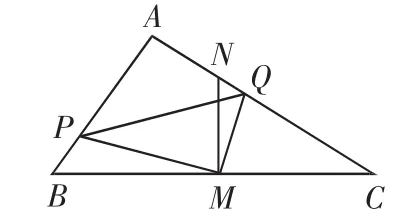
图1

图2(备用图)
二、试题答案展示

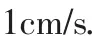


图3

图4
(3)PQ2=BP2+CQ2.理由如下:如图3,延长QM至D,使MD=MQ.连接BD、PD.因为BC、DQ互相平分,所以四边形BDCQ是平行四边形.所以BD∥CQ.因为∠BAC=90°,所以∠PBD=90°.所以PD2=BP2+BD2=BP2+CQ2.因为PM垂直平分DQ,所以PQ=PD.所以PQ2=BP2+CQ2.
三、试题价值分析
(一)试题的概述
本题以三角形为背景,相似为纽带,动态为风向标,全面考查了学生的综合素质能力;题目的设置遵循了从一般到特殊的原则,题目的探究始终围绕△PBM与△QNM相似,从“探究相似——运用相似性质构造方程——根据得到结论解决问题”,每个问题之间环环相扣;注重数学思想的渗透,引导学生从P点运动位置的变化引发分类.
(二)试题解题思路的探究
解决解答题的时候审题是关键,而条件中的关键词又是审题的关键.本题主要抓住点P、Q都是在射线BA与射线NC上运动,而我们在研究的过程中不能同时关注两个动点,那么我们就要分清主动点与次动点,次动点是随着主动点的变化而变化的;再根据射线这个关键词研究主动点P点的位置变化情况.通过研究发现可以分成以下两类:(1)在线段BA上;(2)在线段BA的延长线上.阅卷过程中发现问题“②设△APQ的面积为S(平方厘米),求S与t的函数关系式”的解决学生的错误率非常高,主要原因是学生没有通过射线这个关键词进行分类思想的灵活应用.
【错误答案展示】

(三)审清各个探究问题之间的关系

【错误答案展示】

【正确答案展示】
(3)PQ2=BP2+CQ2.理由如下:如图3,延长QM至D,使MD=MQ.连接BD、PD.因为BC、DQ互相平分,所以四边形BDCQ是平行四边形.所以BD∥CQ.因为∠BAC=90°,所以∠PBD=90°.所以PD2=BP2+BD2=BP2+CQ2.因为PM垂直平分DQ,所以PQ=PD.所以PQ2=BP2+CQ2.
四、中考题试题改编的探究
(一)试题改编的总体意见
试题的呈现过程中应该关注学生的学情,应该要精心打造题目的陈述语言及方式,不要给学生带来不必要的障碍与歧义.
(二)关于“结论”的变式探究
1.探究与△PQM相关的问题
改编题1. 在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N.动点P从点B出发沿射线BA运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP.(1)△PBM与△QNM相似吗?以图5为例说明理由.(2)△PQM与△CNM相似吗?请说明理由.(3)当PM与AC满足什么条件时,△PQM的面积最小?请说明理由.
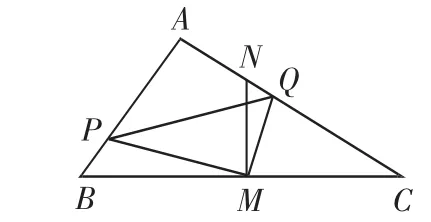
图5

图6(备用图)
【设计意图】第(2)问将△PBM与△QNM的两组边成比例转化成△PQM与△CNM中的两组对应边成比例;注重了转化的数学思想的考查,而这种平时平时的教学过程强化过,学生解决起来难度不是很大;第(3)问在第(2)问的基础根据相似三角形“两个三角形的面积之比是相似比的平方”可以知道,△CNM的面积是个定值,要想△PQM面积最小就要△PQM与△CNM相似比最小,相似比最小就转化成线段QM最小,然后根据垂线段最短确定具体的位置,然后求出此位置的相关数据.
2.探究与四边形APMQ相关的问题
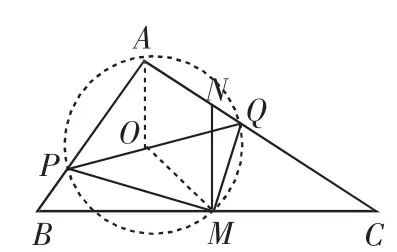
图7
改编题2.如图7,在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N.动点P从点B出发沿射线BA以每秒厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP.设运动时间t秒(t>0)(.1)△PBM与△QNM相似吗?以图5为例说明理由(.2)若∠ABC=60°,AB=4厘米.①求动点Q的运动速度;②如图7,取PQ的中点O,连接AO、MO,我们通过“直角三角形斜边的中线等于斜边的一半”可以证明OA=OQ=OM=OP,这样我们就可以发现A、P、M、Q四点的圆始终在同一个圆上,在P、Q两点运动的过程中,我们发现⊙O的位置与大小都在发生变化,试探究当t为何值时,⊙O的面积最小,并求出最小面积.
【设计意图】研究△APQ的面积S与t的关系有些牵强,只能算是考查了列二元一次函数,而且对于得到函数没有进行后续的研究,后面出现的第(3)问有些唐突,还不如就避开讨论△APQ的面积,转化成讨论四边形APMQ;设计的问题通过叙述证明四点共圆的过程,让学生感受到⊙O的存在性,从而根据变化中不变量点A、M确定圆的最小值;再求时间t的过程时,在Rt△APQ中运用勾股定理构造关于t的方程,又考查了学生在研究动态问题时如何对变量进行表达.
