等腰三角形中的漏解、多解和错解
2012-08-28山东省莱西市第四中学崔明月
☉山东省莱西市第四中学 崔明月
等腰三角形中的漏解、多解和错解
☉山东省莱西市第四中学 崔明月
等腰三角形中关于边角求解的分类讨论问题,一直是令同学们头疼的一个问题,有时忘记分类讨论,导致漏解;有时得出两个答案,又因没有检验是否满足三角形内角和定理和三边关系,导致多解.下面我们举例分析这类问题,看其有何规律.
一、关于等腰三角形角度的求解
例1 若等腰三角形有一个角是70°,则其他两个角的度数是_______.
答案:55°和55°;40°和70°
例2 若等腰三角形有一个角是120°,则其他两个角的度数是_______.
答案:30°
例3 若等腰三角形有一个角是60°,则其他两个角的度数是_______.
答案:60°和60°
规律总结:已知等腰三角形一个角的度数,根据等腰三角形两底角相等和三角形内角和定理可以求出其他两角的度数,什么情况下有两解?什么情况下只有一个解?当等腰三角形一个内角为钝角(如例2)或直角或60°的角(如例3)的时候,求其余各角只有一个解;当等腰三角形的一个内角为锐角且这个锐角(如例1)不等于60°时,求其余各角有两解.
二、关于等腰三角形边的求解问题
例4 等腰三角形的两边长分别为3cm和7cm,则它的周长为________.
答案:17cm
例5 等腰三角形的周长是16,若其中一边长是5,那么另外两边长分别是________.
答案:6、5或5.5、5.5
规律总结:已知等腰三角形的两边(没有指明底和腰时)求其另一边或其周长,可根据等腰三角形的定义求得,什么情况下有两解?什么情况下只有一个解?根据三角形三边的关系,检验求得的两组结果是否满足“两腰之和大于底边”,来判断解的情况.(如例4中,三边可为3cm、3cm、7cm或7cm、7cm、3cm,但是“3cm、3cm、7cm”不满足三边关系,所以答案是一个解;例5的两个结果满足三角形的三边关系,所以是两组解).
下面我们看看这两条规律在运用中出现的问题.
1.漏解
例6 已知等腰三角形的两边长分别为4和6,则该等腰三角形的周长为__________.
错解:该等腰三角形的周长为16.
剖析:由于题目中并没有明确4和6谁是底边长、谁是腰长,所以应分以下两种情形考虑.
⑴当底边长为6、腰长为4时,该等腰三角形的周长为14.⑵当底边长为4、腰长为6时,该等腰三角形的周长为16.同学们只想到了情形⑵,因而导致漏解.正解:该等腰三角形的周长为14或16.例7 等腰三角形的一个角是80°,则它的另两个角是__________.
错解:它的另两个角分别为50°、50°.
剖析:因为题中并未指明80°的角是顶角还是底角,所以应分以下两种情况全面分析.
(1)当80°的角是顶角时,该等腰三角形的底角是50°.
(2)当80°的角是底角时,该等腰三角形的另两个角中,一个角是底角,度数为80°,另一个角是顶角,其度数为180°-80°×2=20°.
正解:该等腰三角形的另两个角分别为50°、50°或80°、20°.
2.多解
例8 已知等腰三角形的两边长分别为3和6,则该等腰三角形的周长为____________.
错解:该等腰三角形的周长为12或15.
剖析:(1)当该等腰三角形的腰长为6、底边长为3时,其周长为15.
(2)当该等腰三角形的腰长为3、底边长为6时,根据“三角形两边之和大于第三边”,可知周长为12这种情形是不存在的,因此这里的“12”是多余的.
正解:该等腰三角形的周长为15.
例9 已知等腰三角形ABC的一个外角是80°,则与它不相邻的一个内角的度数是______.
错解:与它不相邻的一个内角的度数是40°或100°.
剖析:“等腰三角形ABC的一个外角是80°”中的外角只能是与顶角相邻的外角,不可能是与底角相邻的外角.若它是与底角相邻的外角,则两底角都应是100°,这就会使得△ABC的内角和大于180°,这与“三角形内角和等于180°”矛盾,因此这里的“100°”是多余的解.
3.错解
例10 由等腰三角形ABC的顶点A引腰BC边上的高AD,其长恰好等于腰BC长的一半,试求∠BAC的度数.
错解:如图1,△ABC中,AB=AC,AD⊥BC.
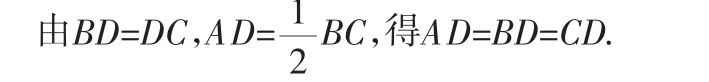
所以∠B=∠BAD=45°,∠C=∠CAD=45°,所以∠BAC=90°.
剖析:错解误将“顶点A”当作“顶角A”,因此而出错.这就要求我们在解题时必须认真读题,深入审题,正确地理解题意.由于题中已指明BC为腰,所以这里的顶角应是∠B或∠C.
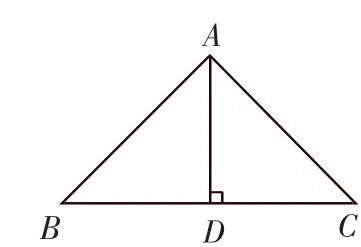
图1
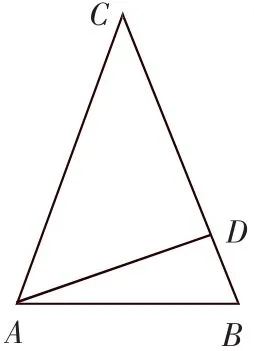
图2
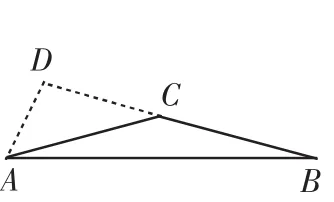
图3
正解:不妨设∠C为顶角.
(1)当高AD在三角形内部时(如图2).

(2)当高AD在三角形外部时(如图3).
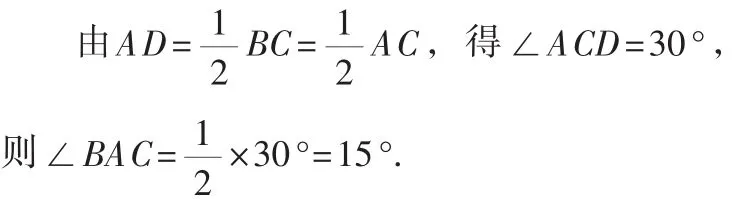
注意:对于此题,如果只考虑高AD在三角形内部的情况,则会出现漏解的错误.
通过上面的例子可以看出,在解决等腰三角形的边、角计算问题时,我们一定要认真分析题目中已知的边和角,分清是哪两个角相等,哪两条边相等,并注意是一解还是两解,防止多解、漏解、错解.
