探索函数与四边形的存在性

☉江苏省东台市实验中学教育集团 吴智勇

探索函数与四边形的存在性

☉江苏省东台市实验中学教育集团 吴智勇

置几何中的四边形于直角坐标系中，借助函数的知识，数形结合，研究具有某种特殊性质四边形的存在性，是2012年中考中出现频率较高的一类综合题.本文从2012年中考题中选取数例，说明这类综合题解题思路的分析方法.

图1

例1 （2012年福建省泉州市）如图1，点O为坐标原点，直线l绕着点A（0,2）旋转，与经过点C（0,1）的二次函数y=x2+h交于不同的两点P、Q.

（1）求h的值.

（2）通过操作、观察算出△POQ面积的最小值.

（3）过点P、C作直线，与x轴交于点B，试问：在直线l的旋转过程中四边形AOBQ是否为梯形？若是，请说明理由；若不是，请指明其形状.试题解析：（1）将点C（0,1）代入二次函数y=x2+h中，得h=1.

（2）操作、观察可知当直线l∥x轴时，其面积最小.将y=2代入二次函数y=x2+1中，得x=±2.

（3）由特殊到一般.

①当直线l∥x轴时，P（－2,2），Q（2,2），直线PC：y=－x+1交x轴于B（2,0）.又A（0,2），所以四边形AOBQ为正方形.

②如图2，当直线l不平行于x轴时，四边形AOBQ为梯形.

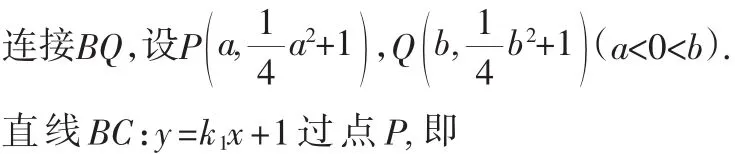
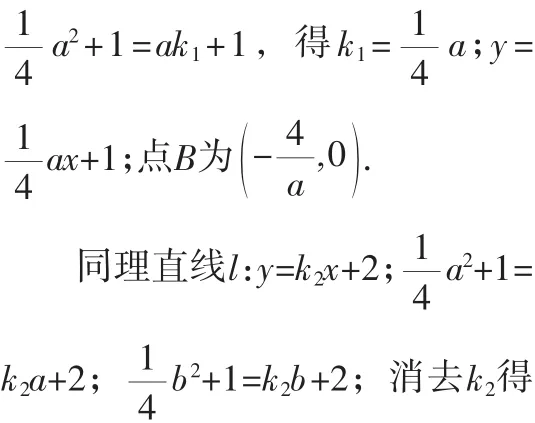
图2

所以点Q、B的横坐标相同，即AC∥BQ，且AQ不平行OB，故四边形AOBQ为梯形

方法点评：数学课程标准中指出：“有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学习数学的重要方式.”因此操作实践型中考题将会从简单的剪剪拼拼向通过操作或实验来探究、发现、猜想等过渡，同时也可能利用操作探究得出的结论来解决新问题，这个动向要引起注意和重视.本题就是一个典型的动手操作实践题，通过动手操作试验，仔细观察，冷静思考，多画几个图形，读几遍题目就会找到解决问题的突破口，另外考虑一定要全面，千万不能多解.

例2（2012年贵州省安顺市）如图3所示，在平面直角坐标系中，矩形OABC的边长OA、OC分别为12cm、6cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线y=ax2+bx+c经过点A、B，且18a+c=0．

（1）求抛物线的解析式.

（2）如果点P由点A开始沿AB边以1cm/s的速度向终点B移动，同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动．

①移动开始后第t秒时，设△PBQ的面积为S，试写出S与t之间的函数关系式，并写出t的取值范围.

②当S取得最大值时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形？如果存在，求出R点的坐标；如果不存在，请说明理由．

图3

②当t=3时，S取得最大值9，这时点P的坐标（3,－12），点Q的坐标为（6，－6）.

若以P、B、Q、R为顶点的四边形是平行四边形，有如下三种情况：

（i）当点R在BQ的左边，且在PB下方时，点R的坐标为（3，-18），将（3，-18）代入抛物线的解析式中，满足解析式，所以存在，点R的坐标就是（3，-18）.

（ii）当点R在BQ的左边，且在PB上方时，点R的坐标为（3，-6），将（3，-6）代入抛物线的解析式中，不满足解析式，所以点R不满足条件.

（iii）当点R在BQ的右边，且在PB上方时，点R的坐标为（9，-6），将（9，-6）代入抛物线的解析式中，不满足解析式，所以点R不满足条件.

综上所述，点R的坐标为（3，-18）.

方法点评：本题在已知三点位置时，探索抛物线上的一点与已知的三点组成平行四边形，解决的方案是先弱化条件，探索平面上的一点与已知的三点组成平行四边形，再验证这一点是否在抛物线上，在则留下，不在则舍去，这种解题思想值得同学们细细品味.另外，说抛物线上的点R与P、B、Q三点组成平行四边形，由于没有指明顶点的顺序，所以要分情况一一说明.

例3（2012年山东省烟台市）如图4，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）.以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发，沿线段AB向点B运动.同时动点Q从点C出发，沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.

（1）直接写出点A的坐标，并求出抛物线的解析式.

（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？

（3）在动点P、Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C、Q、E、H为顶点的四边形为菱形？请直接写出t的值.

试题解析：（1）根据矩形的性质写出点A的坐标，由顶点A的坐标设该抛物线的顶点式为y=a（x－1）2+4，然后将点C的坐标代入，即可求得系数a的值.

A（1，4）.由题意可设抛物线解析式为y=a（x－1）2+4.

由抛物线过点C（3，0），得0=a（3－1）2+4，解得a=－1.

所以抛物线的解析式为y=－（x－1）2+4，即y=－x2+2x+3.

（2）由于A（1，4），C（3，0），可求得直线AC的解析式为y=－2x+6.

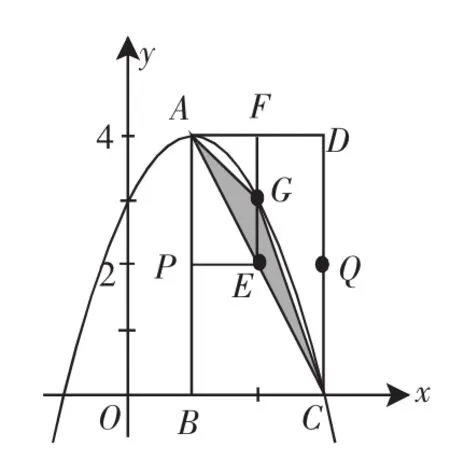
图4

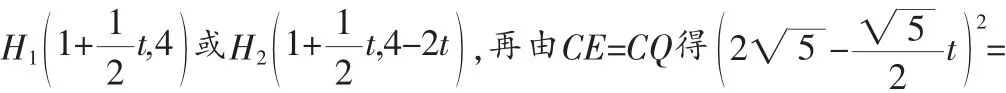
例4 （2012年福州市）如图5，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ.点P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0）.

图5

图6

（1）直接用含t的代数式分别表示：QB=______，PD=______.

（2）是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由.并探究如何改变点Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度.

（3）如图6，在整个运动过程中，求出线段PQ的中点M所经过的路径长.

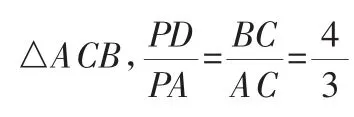
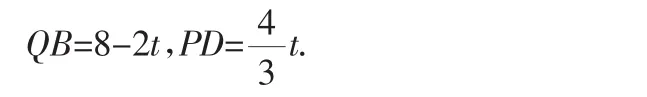
（2）由△APD∽△ACB，即可求得AD与BD的长.由BQ∥DP，可得当BQ=DP时，四边形PDBQ是平行四边形，即可求得此时DP与BD的长.由DP≠BD，可判定▱PDBQ不能为菱形.然后设点Q的速度为每秒v个单位长度，要使四边形PDBQ为菱形，则PD=BD=BQ，列方程即可求得答案.不存在.

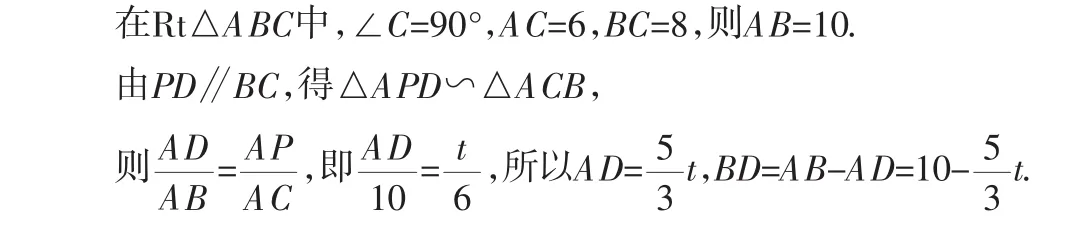
由BQ∥DP，得当BQ=DP时，四边形PDBQ是平行四边形，

（3）是命题人设计本题的亮点，也是学生答题的难点.平时我们可利用几何画板动态演示功能，不难看出线段PQ的中点M所经过的路径是一条线段，在考场上学生必须借助平时积累的学习经验，灵机一动，大胆猜想结论，小心验证结论.

如图7，以C为原点，以AC所在直线为x轴，建立平面直角坐标系.

依题意，可知0≤t≤4，当t=0时，起点M1（即点E）的坐标为（3，0）；

当t=4时，终点M2（即点F）的坐标为（1，4）.

设直线EF的解析式为y=kx+b.

直线EF的解析式为y=－2x+6.

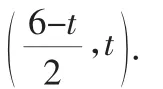
图7

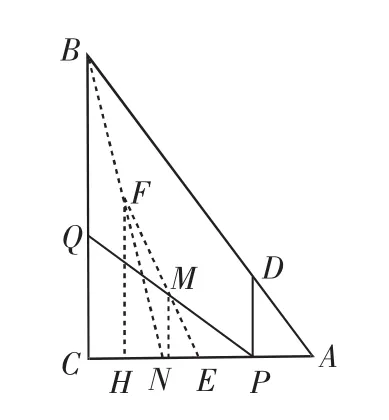
图8

另解：如图8，设E是AC的中点，连接ME.

当t=4时，点Q与点B重合，运动停止.

设此时PQ的中点为F，连接EF.

过点M作MN⊥AC，垂足为N，则MN∥BC.

tan∠MEN的值不变，则点M在直线EF上.

过F作FH⊥AC，垂足为H，则EH=2，FH=4.

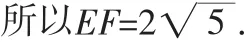
当t=0时，点M与点E重合；当t=4时，点M与点F重合.

方法点评：试题通过点P的运动，带来四边形的运动，把观察、操作、探究、计算融合在一起，将勾股定理、相似三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质以及一次函数的综合应用等初中数学的主干知识融为一体，作为压轴题.本题的设计新颖，不落俗套，自然流畅，梯度合理，入口宽，出口窄，需要综合运用核心知识灵活地解决问题.在探究图形变化过程中，考查了函数思想、方程思想等重要的数学思想方法以及基本轨迹的识别与应用.