解决一元二次方程根的分布问题的基本策略

☉湖南省永州市第一中学 唐长轩

一元二次方程根的分布问题一直是高中数学中的重要内容，由于它常和其他知识形成交汇，近年来一直是高考中的热点，然而在解答过程中大家往往因为思考问题不全面而出错，因而这个内容对大家来说是一个难点.下面就以一道常见的习题为例谈谈解决这类问题的基本策略.

题目：关于x的方程x2+（m－1）x+1=0在区间［0，2］上有解，求实数m的取值范围.

一、数形结合

解法1：令f（x）=x2+（m－1）x+1.方程x2+（m－1）x+1=0在［0，2］上有一解，f（0）=1>0，得f（2）≤0，则在［0，2］上有两解，则解得≤m≤－1.综上可知m≤－1.

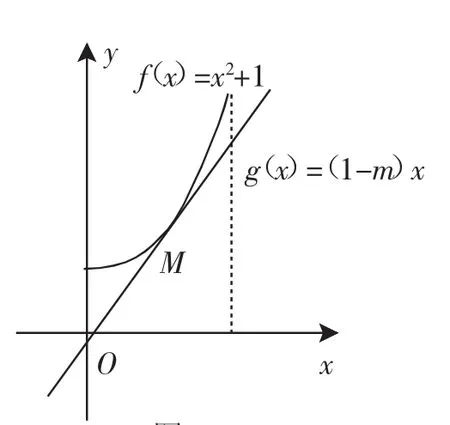
图1

解法2：x2+（m－1）x+1=0化为x2+1=（1－m）x，则由题意可知函数f（x）=x2+1的图像与g（x）=（1－m）x的图像在x∈［0，2］时有交点.易由导数知识求得抛物线f（x）=x2+1的过原点的切线方程为y=2x（y=－2x舍去），切点是（1，2），只需直线g（x）=（1－m）x的斜率1－m满足1－m≥2即m≤－1时，f（x）=x2+1的图像与g（x）=（1－m）x的图像在x∈［0，2］时一定有交点，故方程x2+（m－1）x+1=0在区间［0，2］上有解时，m≤－1.

二、正难则反

解法3：先求出该方程在区间［0，2］上无解时实数m的取值范围，再在实数集R上取其补集.易知原方程在区间［0，2］上无解，则有三种情形：如图1、2、3所示.

图3 图4

若为图1，则△<0⇒（m－1）2－4<0，即－1

取三种情况的并集，得m>－1.故所求m的取值范围为（-∞，-1］.

三、等价转化

最后要特别强调的是以上几种策略并不是孤立的，它们往往相互渗透，在解决一个问题时会用到多种方法.