高中数学示错教学的 实 践 与 研 究
2012-08-28浙江省桐乡市高级中学丰关堂
☉浙江省桐乡市高级中学 丰关堂
在数学教学中,我们经常发现许多学生在学习中并不是不勤奋也并不是不够聪明,而是因为常常忽略了一些细节问题导致学习效果不佳.示错教学能够将一些学生理解得不够透彻和没有注意到的地方特别强调出来,帮助学生提高对数学知识的理解和运用.本文主要阐述示错教学在高中数学教学中的作用和重要性.
一、示错教学的界定、目的、意义及理念支撑
“示错”即是“展示错误”.但是示错教学并不只是简单地将错解展示在学生面前.而是教师通过对学生所犯错误的观察,选择典型的错例,但并不直接指出学生的错误,而是让学生表述在解题时的思路和想法,根据表述来找出学生犯错误的根源,如对概念理解得不透彻、存在某种思维定势等,进而帮助学生解决问题,避免以后再犯.老师在示错教学中也不仅仅是帮助学生寻找错误、改正错误,还要教会学生如何发现错误、怎样寻找错误的根源并学会自己对自己进行示错教学.
通过这样的示错教学,学生收获的不仅仅是改正一道题或是一类题,而是培养正确的解题方式、思维习惯和反思的能力.这种良好的习惯不仅对学习数学有益,对学习其他学科乃至为人处事都大有裨益.
数学发展的历史就是数学家们通过不断犯错,又不断地发现并改正错误,在众多岔路口中最终寻找到通往真理道路的过程.因此,我们要帮助学生正确认识数学学习中所犯的错误,不能不当回事,也不能对数学丧失信心,让这些错误不仅不会成为学生们前进的绊脚石,反而成为学生前进的阶梯.
二、示错教学的操作方法
1.全面理解定义、定理和公式.
在数学学习中,定义、定理和公式是解决一切问题的基石.如果连数学的基本概念都没有理解透彻,对适用范围也没有理清,对概念与概念之间的相互联系都不能很好把握,在解决一两个问题时也许没有体现出来,但随着解决的问题数量以及难度的提高,这些缺陷就会暴露出来.不少学生认为要想学好数学、在考试中拿高分就必须努力钻研难题.实际上,很多学生在解决一个所谓的难题时,“卡”住的地方往往就是他对基本概念掌握不牢的地方.
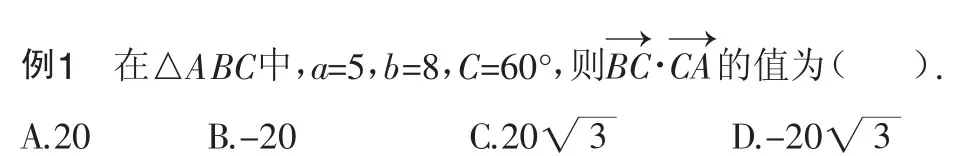
2.找出题目中的陷阱.
有一些高中数学题题干非常长,看起来很复杂,但是实际上做起来比较简单,而有些数学题题干也许只有一句话,看似简单,其实在这一句话中还隐藏了一些表面上没有看到的条件,学生们稍不注意就容易掉入这样的“陷阱”.
这道题看起来比较简单,通过前面的等式变形可以得到y2=-4x2-16x-12,从而可以得到,由这个式子我们可以得到,当时,x2+y2有最大值的取值范围是].可是实际上是这样吗?这样的解法其实默认了x的取值范围为(-∞,+∞),但是我们还忽略了题干中给的另一个隐藏的条件,那就是通过前面的等式,我们可以获得x的取值范围.x的取值范围其实并不是(-∞,+∞),而是通过,可得x的取值范围为[-3,-1].在这个基础上求到的x2+y2的取值范围才是这道题的正解.
例2中的x的取值范围在题干当中,还有另外一种情况如x2≥0、三角函数-1≤sinx≤1这类并不需要在题干中特别提出就已经默认的取值范围情况.因此,在做高中数学题时,要时时刻刻记着任何结论都是在一定的范围内成立的,要随时注意取值范围的问题.要想避开题目中的陷阱,获得真正的答案,就要认真分析题目提供的每个条件,还要注意到题目中所涉及知识点的特殊性,如前所提到的三角函数的取值范围等,常常问自己还有什么方面没有考虑到.
3.分类讨论要严密.
许多学生对数学的印象还停留在只有唯一正解的印象上,如果是选择题,有可能在选项的提示下还会进一步思考,而如果是解答题则常会因为思维的不严密性造成分类讨论不全,忘记讨论特殊情况等现象.
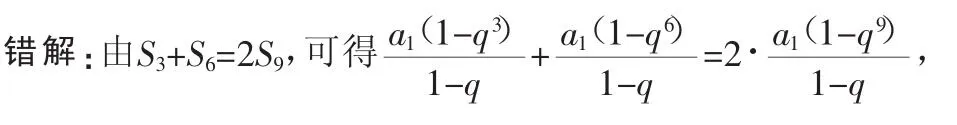
例3 设等比数列{an}的前n项和为Sn,若S3+S6=2S9,求数列的公比q.整理可得q3(2q6-q3-1)=0.由q≠0,可得方程2q6-q3-1=0,即
这个解法虽然得到了正确答案,但解法中却有错误,问题出在哪儿呢?在等比数列中,虽然a1≠0,但是公比q却是可以等于1的.因此在设未知数列出等比数列之前应先讨论q=1的情况,再讨论q≠1时,将所设等式进行变形,而错解中所设的公式已直接除去q=1的情况.
在与数列相关的题中,常需要考虑许多特殊情况,尤其是公比q=1的情况.老师在对这一类题进行示错教学时,不仅要指出学生漏考虑了哪种情况,还可以帮学生总结出一些常见的需要考虑特殊情况的题型.当然,最重要的仍然是要让学生有考虑特殊情况和分类讨论的意识.对于分类讨论的题目,学生失误多是由于没有一个宏观考虑问题的意识,要在对这类题目进行示错教学时培养学生从全局把握问题.
4.摆脱思维定势.
有许多学生看到数学题并没有对整道题有一个全局的把握,头脑中也没有一个完整的思维过程,而是拿起笔就写,这样很容易被题目牵着鼻子走,尤其是遇到一些和以前遇到的题目类型相类似的题目时,更容易陷入一种思维定势,造成解题的错误.
例4 过点P(2,3)且与曲线y=x3-2x+3相切的直线方程.
要求曲线的斜率很简单,即把x=2代入切线的斜率方程,即k=y′|x=2=(3x2-2)|x=2=10,所以所求切线方程为y-3=10(x-2),即10x-y-17=0.
但是这样的解法却是错误的,为什么呢?因为y=f(x)在点P(x0,y0)处的切线的斜率是f′(x0)成立的条件是点P要在曲线上.许多学生在做题的时候看到题目表明是过点P与曲线相切的方程就按照思维定势认为这个点就是切点.实际上在例5中,点P(2,3)虽然在切线上却不在曲线上,点P并不是切点.这是解这类题型时的典型错误,随着老师的强调,现在大部分学生已不会再犯这样的错误.但是思维定势并不仅存在这一类题中,因此学生在做题时切忌按照以往的印象来做题,而是应该认真审题,尤其是遇到与以前做过的题类似的题时更应该谨慎.避免思维定势一个很好的办法就是当自己认为理所应当是这样时再问自己一遍,有没有不是这样的情况.就像这道题,一看题很多学生都想当然认为P是切点,应该问自己,P真的是切点吗?P可不可以不是切点?
三、示错教学的理念提升
前面对示错教学的介绍以及后面列举的几个典型问题似乎都在说明示错教学主要是在向学生展示一道题的错误解法,通过指出错解的原因和需要注意的问题以达到教学的目的.但实际上,对示错教学的认知和应用已不应该仅局限在习题的讲解上,而应将其的深度和广度扩大.在上新课时,以前老师们多是干巴巴地讲解新概念,随后就是一系列的例题讲解.其实,高中数学的学习并不仅仅是通过简单的讲解概念和例题来进行的,在讲解概念时,我们也同样可以应用到示错教学,通过列举几种理解上的错误来帮助理解数学的文字概念.示错教学也不一定要通过老师来进行,毕竟老师不可能将每道错题都一一在课上讲解出来.
在高中数学教学中,示错教学是一个非常有效的教学手段.通过示错教学,学生能更好地发现自己对定义、概念等理解的偏差,发现自己在解题思路,答题策略上的一些疏忽.学生只有真正认识到自己错误的所在,才能及时改正,夯实数学基础,提高数学的应用能力.因此,老师应当根据学生的实际情况以及所犯错误的类型进行适当的示错教学.
