排列问题的“一字诀”

☉浙江省东阳中学 陈立明

排列问题的类型多样、背景丰富、解法灵活多变，是每年高考必考知识点之一.仔细审题，根据已知条件选择恰当的解题技巧与方法是成功解题的关键.下面介绍几种常用的解题技巧与方法.

一、捆

是指把一些要求相邻的元素（或位置）看成一个整体考虑的方法.也可以归纳为口诀：相邻问题“捆绑法”.

例1 3对夫妻排成一列.

（1）甲、乙兄弟2人要求必须排在一起；

（2）3对夫妻都不能分开；

（3）甲、乙两人之间必须间隔1个人.

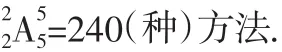
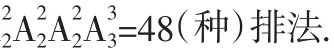
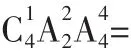
二、插

是指让其他元素（位置）先排列，然后把需要特殊考虑的元素（位置）插入已排好的元素之间的方法.往往用来解决不相邻问题，归纳为口诀：不相邻问题“插空法”.

例2 记者要为5名志愿者和2位老人照相.

（1）甲、乙两人要分开，有多少种？

（2）要求老人不相邻且不坐两端，则不同的排法有多少种？

不相邻问题中有一种特殊问题：相间问题.这类问题的解决与插空法有一定的联系与区别.

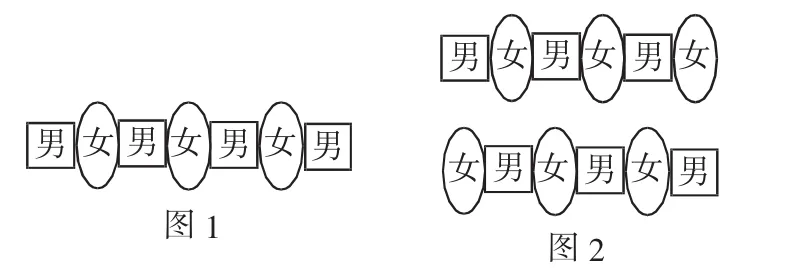
例3 （1）4名男生，3名女生，要求男生、女生都互不相邻，问：有几种排法？

（2）3名男生，3名女生，要求男生、女生都互不相邻，问：有几种排法？

三、除

是指部分元素（位置）的顺序有特殊要求，我们先不做考虑，全排列好后除去这部分元素的所有的排列数的办法.口诀可以归纳为：定序问题用“除法”.

例4A、B、C、D、E五人按先后顺序上车.

（1）若B必须在A前（A、B可以相邻），则不同的排法的种数是多少？

（2）若A、C、E三人已经约定了上车先后次序（三人不一定相邻），则有多少种排法？

（3）若A、B相邻且B必须在A前，则不同的排法的种数是多少？

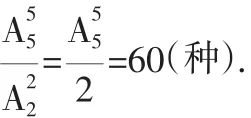
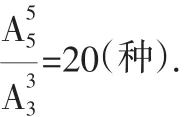
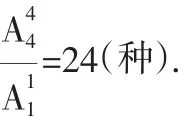
四、减

是指一些要求满足的情况比较复杂，我们把所有不满足条件的排列减去.可以归纳为口诀：正难则反，减去不满足，它是间接法的一种.

例5 一个班级某天要排不同的6门课.

（1）语文老师不喜欢第6节，问：有几种排课方法？

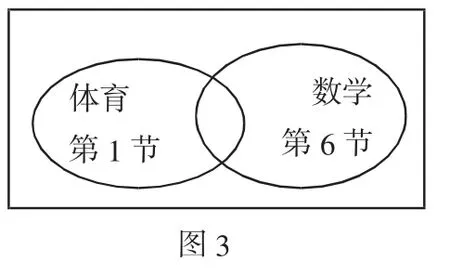
（2）若体育不排第1节，数学不排最后一节，问：有几种排课方法？

五、分

是指比较多的要求要同时满足，为了理清所有要求，我们有针对性地进行分类讨论的方法.口诀是这样的：讨论可把乱理清.

例6 用0、1、2、3、4、5这6个数字组成无重复数字.

（1）有多少个三位偶数？

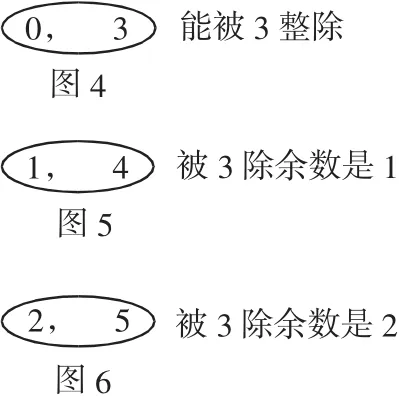
（2）有多少个能被3整除的四位数？

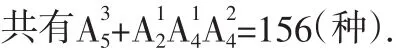
（2）被3整除的三位数的特征是个位、十位、百位、千位的数字之和是3的倍数.可是三个数之和是3的倍数的比较多，通过分类理清思路.

第二类，被3整除的数取1个，这样剩余三个数之和肯定不能被3整除，不存在.

所以总共有96个能被3整除的四位数.

六、隔

是指把所要分配的名额等分隔成若干段，然后每人拿走属于自己的名额的方法.也可以归纳为口诀：名额分配“隔板法”.这种方法应用范围特定，特征明显.

例7 学校决定把12个参观航天航空博物馆的名额给二（1）、二（2）、二（3）、二（4）四个班级.

（1）要求每个班级至少有1个名额，问：有几种分配方案？

（2）要求每个班分得的名额不比班级序号少：即二（1）班至少1个名额，二（2）班至少2个名额，……，问：有几种分配方案？

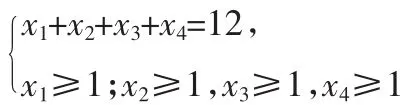
（2）先给二（2）、二（3）、二（4）班各1、2、3个名额，在把剩余的6个名额分配给4个班级，每个班级至少1个，从而把问题变成了隔板模型：6个名额之间形成5个间隙，在5个间隙中任意插入3块隔板，把名额分给4个班级.共=10（种）.