黄沙吹尽 返璞归真——一道习题的多角度探究

☉湖北省宜昌市夷陵中学 徐 勇

学生上完选修4-5《不等式选讲》第二讲“柯西不等式”不久，一个学生拿着一道题来问我，原题如下：

我和这名同学一起分析，觉得要求出u的最小值，去根号是关键，于是有了如下探究：

探究一：由柯西不等式（a2+b2）（c2+d2）≥（ac+bd）2得：

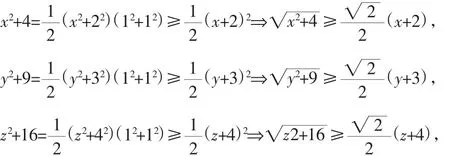
探究二：

和学生一起探究完这道题，感觉这道题能很好地培养学生的观察、分析、辨误、纠误能力，是一道难得的好题，于是决定在习题课上面向全班学生评析此题.

第二天的习题课上，当我按照上面的探究一、探究二讲解完这道题，并再次强调此题构造柯西不等式的思路时，几个学生在下面小声说，这样构造也太麻烦了吧！这句话打消了我接着讲下一题的计划.是啊，像探究一、二这样做确实能解决问题，但付出的代价太大了，还不如发挥学生的主体地位，让学生继续探究下去！于是，我引导道：“还有没有更简单的方法？请大家思考并讨论.”经过热烈的讨论，不少同学举起了手，我点了学生甲，请他到黑板前面让大家分享他的成果，于是有了如下探究：

探究三：考虑到柯西不等式左边有两组平方和相乘，而本题的函数u为三项相加，只要先把u平方即可得到乘积形式，即u2=x2+4+y2+9+z2+16+2 ［8）=（x+y+z）2+81=442，当且仅时等号成立.又u＞0，故umin=

教室里响起了热烈的掌声！探究三充分考虑了柯西不等式的结构特点，求解更为直接.那这道题还有没有别的做法呢？这时学生的思维完全打开了，不久学生乙就给出了另一种方法：

探究四：本题函数u为根式和形式，且被开方数为平方和形式，这一点与二维形式的三角不等式吻合，所以连续两次运用三角不等式即可，

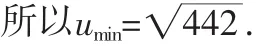
学生乙的做法跳出了柯西不等式的窠臼，根据函数式的整体结构特点进行有效联想，做法漂亮、干脆，令人眼前一亮！当大家还沉浸在这种优美解法中时，学生丙举手站了起来：

探究五：探究四的做法实质就是构造三个向量：a=（x，2），b=（y，3），c=（z，4），，当且仅当向量a，b，c同向共线，即时两等号同时成立.故u

好一句“实质就是”，让我们对函数u有了新的认识.那我们对函数u还能从别的角度去认识它吗？果真是“思想有多远，行动就有多远”，很快学生们就给出了另一种探究思路：

由两点间线段最短有

真是令人拍案叫绝！一道看似需要用柯西不等式才能做的问题，竟然用初中的平面几何知识就轻易解决了！学生们彻底沸腾了……

反思：很多学生包括老师在内都有一种思维定势，认为新课后的作业、习题一定要用新课上的知识去解决，这种观点其实是大错特错的.本案例中，通过放手发动学生去思考，学生不断优化自己的思维，在创造、再创造中得出很多体现了书本知识灵活应用的方法，逐步对问题的本质有了清晰的认识.另外，本次探究成功很重要的一点是有了学生的积极参与.布鲁纳认为：在教学过程中，学生是一个积极的探索者，教师的作用是形成有助于学生独立探究的情境，让学生自己思考问题，参与知识获得的过程.教师要舍得留出时间和空间给学生，以供他们驰骋自己的思维.