例谈利用三次函数模型解决实际问题

☉江苏省兴化市戴南高级中学 赵亚兵

函数是每年高考的必考内容之一，高考在利用函数模型处理实际问题方面的考查有上升趋势，一次函数和二次函数的应用是高考命题的常见题型.然而三次函数也已经成为中学阶段一个重要的函数，在高考和一些重大考试中频繁出现有关它的单独命题.我们通过对近几年高考试题的分析发现：利用三次函数模型处理实际问题成为近年来高考命题的热点之一，题目涉及的三次函数一般都是以其为载体，通过其性质来解释生活现象，主要涉及经济、环保、能源等社会领域.笔者以高考试题的解析来说明如何灵活运用三次函数的性质和特点处理实际问题.

高中数学中由于导数内容的介入，使得研究函数的性质变得简捷、易懂，通过求导可以直接研究函数的单调性和极值，其操作的步骤学生易掌握，判别的方法也不难.尤其是：当f（x）为三次函数时，通过求导得到的f′（x）为二次函数，且原函数的极值点就是二次函数的零点.同时利用导数的几何意义：曲线在某一点P（x0，y0）处的切线的斜率k=f′（x0），可得到斜率k为关于x0的二次函数.根据这些特点，一般三次函数问题，往往可通过求导，转化为二次函数或二次方程问题，然后结合导数的基本知识及二次函数的性质来解决.

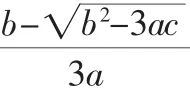
性质1：函数y=ax3+bx2+cx+d（a≠0），若a＞0，当Δ≤0时，y=f（x）是增函数；

当Δ＞0时，其单调递增区间是（-∞，x1］和［x2+∞），单调递减区间是［x1，x2］.

若a＜0，当Δ≤0时，y=f（x）是减函数；当Δ＞0时，其单调递减区间是（-∞，x2］和［x1，+∞），单调递增区间是［x2，x1］.

性质2： 函数（fx）=ax3+bx2+cx+d（a≠0），x∈［m，n］，若x0∈［m，n］，且f（x0）=0，则：f（x）max=max{f（m），f（0），f（n）}；f（x）min=min{f（m），f（x0），f（n）}.

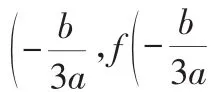
下面通过一道高考试题来说明利用三次函数性质来处理实际问题.

（1）求a的值；

（2）若该商品的成品为3元/kg，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大.

商场每日销售该商品所获得的利润为：

f′（x）=10 ［（x-6）2+2（x-3）（x-6）］-30（x-4）（x-6）.令f′（x）=0，得x=4.

函数f（x）在（3，4）上单调递增，在（4，6）上单调递减.

当x=4时，函数f（x）取得最大值f（4）=42.

当销售价格x=4时，商场每日销售该商品所获得的利润最大，最大值为42元.

点评与反思：本题主要考查函数模型的选择与应用，利用导数研究三次函数的单调性从而解决实际生活中的优化问题.第二问中，商场每日销售该商品所获得的利润=每日的销售量×销售该商品的单利润，得出日销售量的利润函数为关于x的三次多项式函数，再用求导数的方法讨论函数的单调性，得出函数的极大值点，从而得出最大值对应的x值.

总之，利用三次函数模型处理实际问题的关键是：先掌握三次函数的三条性质，然后用导数作为工具来研究函数的单调性和极值.由于三次函数的导函数是二次函数，因此，考查三次函数能把导数的有关知识和二次函数的问题巧妙地结合起来，具有一定的综合性和很好的区分度，所以，全面认识三次函数的图像与性质，对于备战高考意义重大，同时也有助于提高对知识系统性的理解水平，拓宽解题思路.