引入侧向加速度反馈的侧滑转弯控制方法

杨黔龙，周凤岐

（西北工业大学精确制导与控制研究所，陕西 西安 710072）

0 引言

大展弦比滑翔增程弹由于具有重量轻、成本低、飞行距离远等特点，近年来，通过加装大展弦比弹翼组件使低成本常规弹药具备防区外打击能力一直是国内外研究的热点。由于这种面对称结构的弹体大侧滑飞行时斜吹力矩很大，如果再叠加上低成本弹翼加工误差以及其它未知干扰而引起的滚转力矩，容易导致滚转舵饱和，造成滚转控制的困难。所以，大展弦比面对称布局弹体大多都在中制导段采用BTT（倾斜转弯）控制，以减小侧滑，降低滚转控制的负担［1］。然而，BTT控制的特点决定了BTT导弹是一个强耦合的非线性时变系统，为其控制系统设计增大了难度［2－5］；其次，BTT控制对于小的过载指令也可能会产生大的滚转角和滚转角速度指令，容易导致滚转通道的剧烈抖动；另外，BTT还存在控制时延的问题，在接近目标的弹道末段，通常需要切换到STT（侧滑转弯）模式以提高命中精度［6］，这进一步增加了控制系统的复杂度。因此，通过分析STT和BTT两种控制模式的优缺点，本文提出了一种大展弦比滑翔增程弹自动驾驶仪倾斜通道引入侧向加速度反馈的STT控制方法。

1 自动驾驶仪控制技术

自动驾驶仪是导弹的中枢指挥系统和稳定控制系统的核心，一般由惯性器件、控制电路和舵系统组成，并与导弹弹体动力学系统及气动舵面一起构成导弹稳定控制系统。飞行中，驾驶仪敏感导弹自身在控制与干扰作用下运动状态变化，并据此作出响应，操纵导弹气动舵面和发动机推力，使导弹按制导指令机动［7］。根据导弹机动方式的不同，驾驶仪分为以下两类：1）STT驾驶仪，即按照直角坐标来控制弹体飞行，导弹转弯时不滚转，倾斜角保持为零，转弯所需的侧向过载由侧滑角产生；2）BTT驾驶仪，即按照极坐标体制来控制弹体飞行，导弹转弯前先通过滚转通道控制弹体快速旋转，尽快将导弹的主升力面对准目标，然后操纵弹体俯仰通道迅速跟踪导引指令，整个过程侧滑角保持为零（一般指标要求是不大于3°）［8－9］。

目前，大多数导弹采用的是STT控制技术，其STT驾驶仪由俯仰、偏航、倾斜三个独立通道构成，典型结构如图1所示。STT驾驶仪的俯仰和偏航通道结构相同，由阻尼回路、伪攻角回路和加速度控制回路组成，实现法向加速度控制；倾斜通道由滚转角速率阻尼回路和滚转角控制回路组成，实现倾斜角稳定［10］。

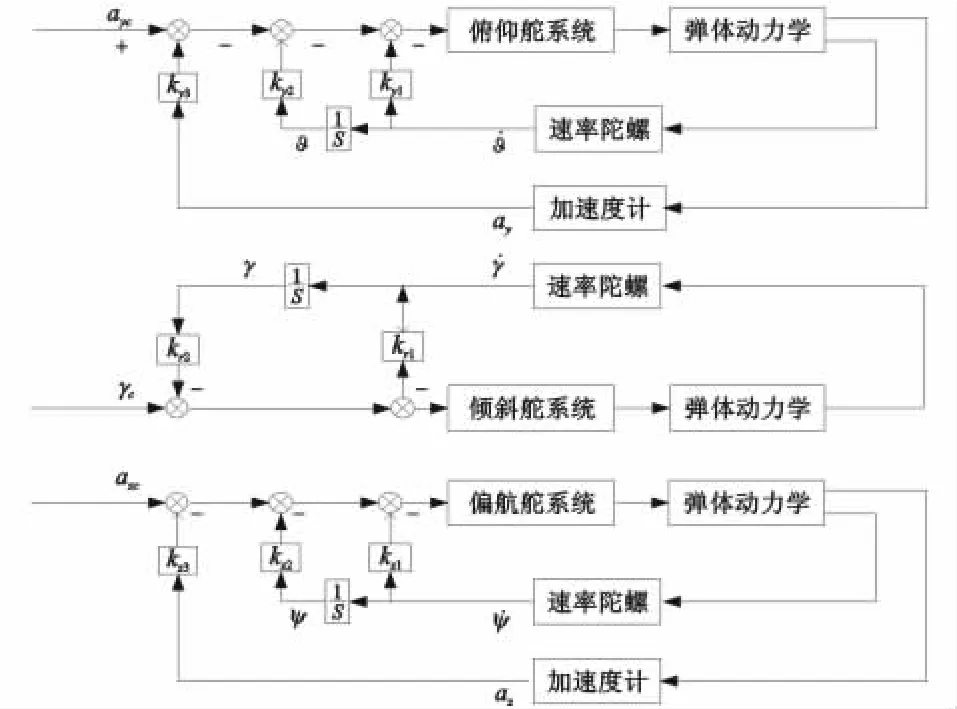
图1 STT驾驶仪原理图Fig.1 Schematic of the STT autopilot

传统STT导弹倾斜通道需要保持倾斜角γ＝0，并通过侧滑产生的侧向加速度az来实现侧向转弯，即

式（1）中，Z 为侧向力，Cβz为侧向力系数，β 为侧滑角。

2 引入侧向加速度反馈的侧滑转弯控制

由于大展弦比面对称弹体侧向力系数Cβz往往较小，而滚转力矩系数Mβx又相对较大，采用图1的STT控制模式容易导致侧向机动与倾斜稳定之间的矛盾难以协调，造成滚转控制的困难。

为解决以上问题，在STT驾驶仪的倾斜通道中引入以下侧向加速度反馈：

式（2）中，k为侧向加速度反馈系数。

引入侧向加速度反馈后，实现了倾斜角对侧向加速度的跟随，水平转弯时弹体向心力为：

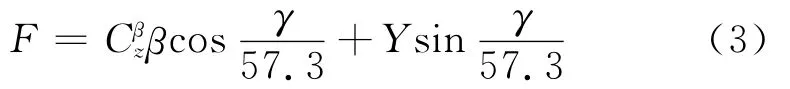
为了避免各通道之间产生严重耦合，确保三通道独立设计的合理性，倾斜角被严格限制于较小的范围内（本文限制在15°以内），式（3）可简化为

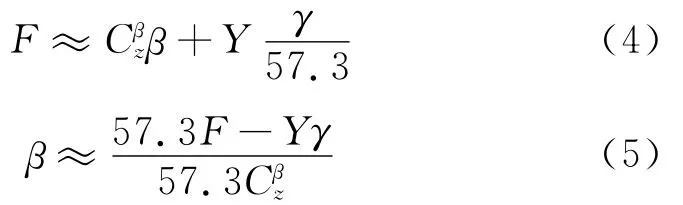
假设某转弯过程向心力F与弹体升力Y为确定值，当侧向加速度反馈系数k增大时，倾斜角γ随着指令γc增大，所需的侧滑角就会相应变小。

如果侧向加速度反馈系数k＝0，则γc＝0，控制系统为典型的传统STT模式

如果β＝0时，即向心力完全由弹体升力Y在机动平面上的投影提供，控制系统相当于BTT模式

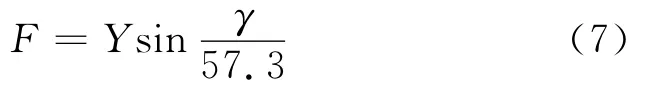
引入侧向加速度反馈后，控制系统根据侧向加速度的大小自动调整弹体倾斜角度，此时，必须对俯仰通道进行高度补偿，以避免飞行过程中出现掉高现象。高度补偿比较简单，此处不再详述。

引入侧向加速度反馈的STT驾驶仪，相当于在传统的STT控制系统上增加了BTT的控制效果，实现了两种控制模式的有机组合，其结构如图2所示。

图2 引入侧向加速度反馈的STT自动驾驶仪Fig.2 STT autopilot employ lateral acceleration feedback

3 六自由度非线性仿真验证

3.1 仿真模型

根据滑翔增程弹的非线性运动方程，采用模块化建模的思想，将系统划分为功能相对独立的大气环境、重力加速度、力和力矩、弹体平动运动、弹体转动运动、舵系统、攻角侧滑角解算、坐标变换矩阵以及三通道控制等功能模块，再对这些功能模块进行集成，构建的六自由度非线性仿真总体模型如图3所示。

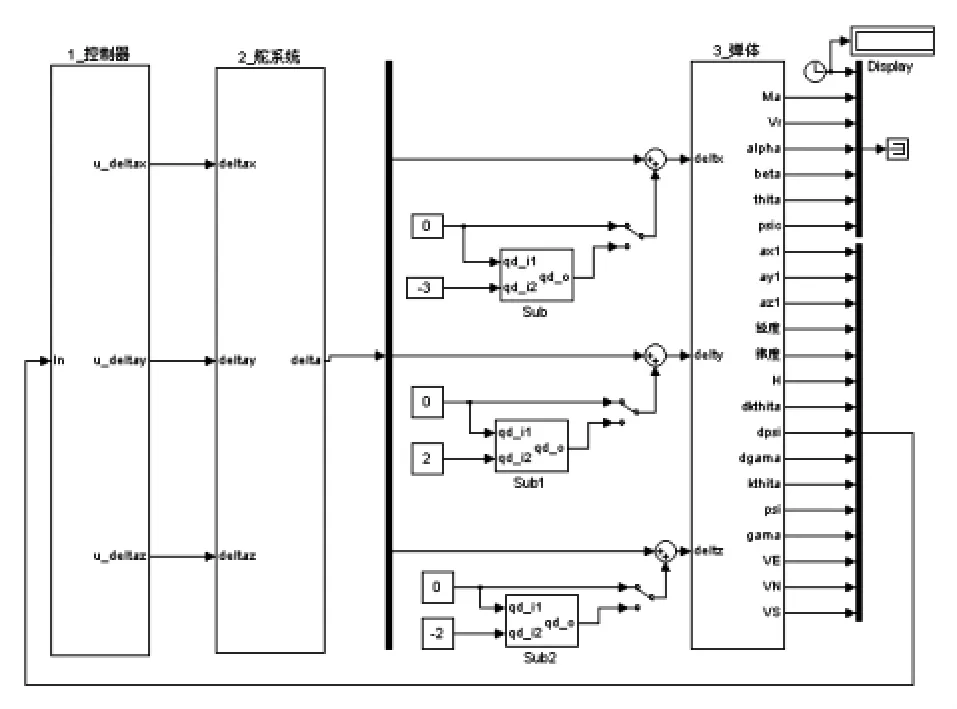
图3 六自由度非线性仿真模型Fig.3 Six-DOF nonlinear si mulation model

3.2 仿真实验条件

滑翔弹投弹高度4 800 m，初始速度为水平方向220 m／s，垂直方向－4 m／s，初始位置误差为侧向左偏300 m。第2.75 s弹翼展开到位后接入侧向加速度反馈，并施加3°滚转干扰舵偏。考虑到风洞实验数据存在误差，滚转舵效拉偏－10%。

3.3 驾驶仪控制指令

为了模拟某空地导弹的飞行过程，滑翔弹纵向弹道按指数下降并在3 000 m高度转入平飞，俯仰通道加速度指令为

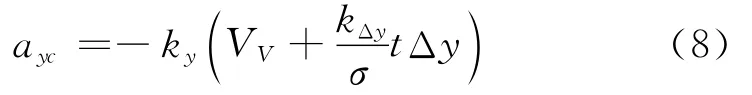
式（8）中，ky和kΔy为控制增益，Δy的表达式如下：

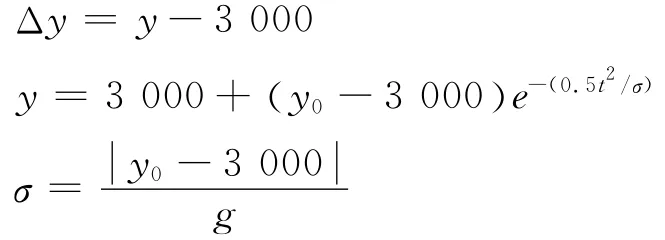
偏航通道加速度指令为

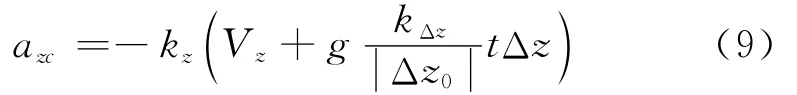
式（9）中，kz和kΔz为控制增益，Δz和Vz、Δz0分别为侧偏距、侧向速度以及侧向投弹偏差，其计算过程参考文献［3］。

末弹道由于侧滑较小，不需要引入侧向加速度反馈，导引律采用带落角约束的增广比例导引，详情参考文献［11］。

3.4 仿真实验结果分析

根据以上的六自由度模型、控制指令以及实验条件进行仿真，结果如图4—图9所示。k＝0表示未引入侧向加速度反馈，即传统STT控制模式下的弹道参数；k＝3表示引入侧向加速度反馈，且反馈系数为3时的弹道参数。图4—图6表明，两种控制模式下纵向、侧向弹道以及飞行攻角完全一致，这说明这三项参数主要取决于纵向及偏航控制律设计，滚转通道引入侧向加速度反馈后，原有的飞行轨迹未受影响。

图7—图9是有无侧向加速度反馈两种情况下弹体的倾斜角、侧滑角以及滚转舵偏对比。当k＝0，即未引入侧向加速度反馈的情况下，弹体倾斜角一直维持在零度附近，其STT转弯过程的向心力全部由Cβzβ提供，导致最大侧滑角达到了3.8°，为了平衡大侧滑以及干扰舵偏产生的滚转力矩，需要很大的滚转控制力矩以致滚转舵达到饱和（限幅15°），此时，如果再叠加上其他未知干扰，将进一步增加滚转控制的难度。当k＝3，即引入侧向加速度反馈后，实现了倾斜角对侧向加速度的跟随，滚转通道产生了最大为4°的倾斜角，此时，控制系统相当于STT与BTT的组合，飞行过程的最大侧滑角减小到2.2°，与此同时，最大滚转舵偏减小到10°。从上述仿真结果可知，大展弦比滑翔增程弹STT驾驶仪倾斜回路引入侧向加速度反馈后，降低了飞行过程的侧滑角，并使滚转舵偏远离饱和状态，执行机构因此有较大的裕度去克服各种未知干扰，提高了滚转控制的能力。

图4 纵向弹道Fig.4 Longitudinal trajectory

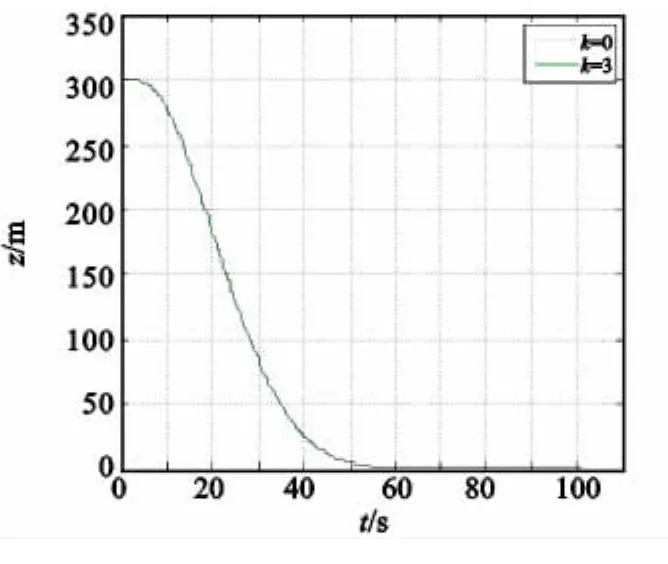
图5 侧向弹道Fig.5 Lateral trajector y

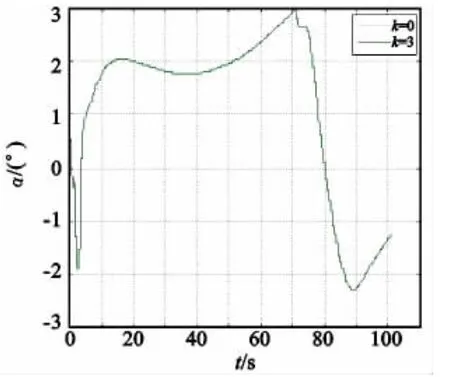
图6 攻角Fig.6 Attack angle

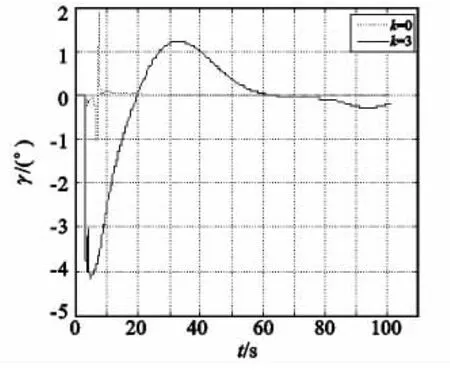
图7 倾斜角Fig.7 Roll angle

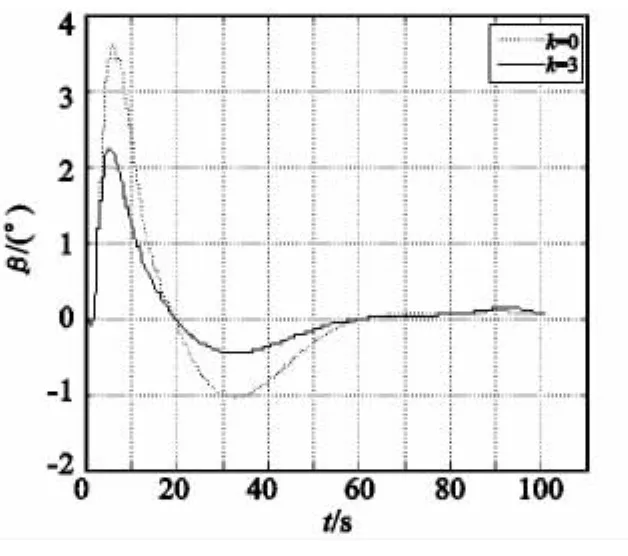
图8 侧滑角Fig.8 Sideslip angle

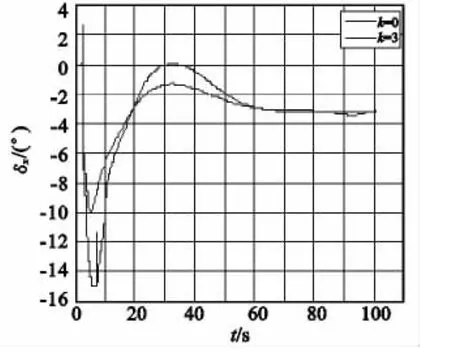
图9 滚转舵偏Fig.9 Roll rudder deflection angle

研究表明：随着反馈系数k的增大，最大倾斜角逐渐增大，最大侧滑角逐渐减小，滚转舵偏也随之减小，然而，反馈系数过大时，各通道之间的耦合效应进一步增强，将引起系统振荡甚至发散。反馈系数k需根据飞行要求经多次仿真后确定［12］。

4 结论

本文提出了一种大展弦比滑翔增程弹自动驾驶仪引入侧向加速度反馈的STT控制方法。该方法通过在传统STT驾驶仪倾斜回路引入侧向加速度反馈，实现了倾斜角对侧向加速度的跟随，相当于在传统的STT控制系统上增加了BTT的控制效果。六自由度非线性仿真实验表明：STT驾驶仪倾斜回路引入侧向加速度反馈后，降低了侧滑角，并使滚转舵偏远离饱和状态，提高了驾驶仪滚转控制的裕度。该项技术可以应用于大展弦比滑翔增程弹以及其他具有大展弦比面对称结构气动布局的飞行器控制。

［1］崔生旺.巡飞攻击导弹制导控制系统研究［D］.北京：北京理工大学，2007.

［2］于秀萍.基于动态逆系统的神经网络理论的BTT导弹控制系统研究［D］.哈尔滨：哈尔滨工程大学，2004.

［3］郑建华，杨涤.鲁棒控制理论在倾斜转弯导弹中的应用［M］.北京：国防工业出版社，2001.

［4］张友安，胡云安.导弹控制和制导的非线性设计方法［M］.北京：国防工业出版社，2003.

参考文献：

［5］董翔宇，任利，刘云飞，魏晓兰.BTT导弹变结构自适应控制仿真研究［J］.计算机仿真，2009，26（11）：65-68.DONG Xiangyu，REN Li，LIU Yunfei.Si mulation of BTT missile based on variable structure adaptive control［J］.Co mputer Si mulation，2009，26（11）：65-68.

［6］庞瑞，史忠科.导弹混合BTT／STT变结构控制器设计与仿真［J］.弹箭与制导学报，2009，29（1）：23-26 PANG Rui，SHI Zhongke.Missile variable str ucture controller design with hybrid BTT／STT logic［J］.Jour nal of Pr ojectiles，Rockets，Missiles and Guidance，2009，29（1）：23-26.

［7］魏喜庆.基于神经网络的BTT导弹自动驾驶仪设计［D］.哈尔滨：哈尔滨工业大学，2007.

［8］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学出版社，2008.

［9］杨军.导弹控制原理［M］.北京：国防工业出版社，2010.

［10］杨军.导弹控制原理［M］.北京：国防工业出版社，2010.

［11］王洪强.某滑翔增程靶弹弹道设计与控制系统研究［D］.上海：上海交通大学，2012

［12］YANG Qianlong，HU Juanzhao.Design and simulation of the rolling loop for a gliding missile with high aspect ratio wings［J］.American Journal of Engineering and Technology Research，2011，11（9）：387-393.