A FAST LAGRANGIAN SIMULATION METHOD FOR FLOW ANALYSIS AND RUNNER DESIGN IN PELTON TURBINES*

ANAGNOSTOPOULOS John S., PAPANTONIS Dimitris E.

School of Mechanical Engineering, National Technical University of Athens, Greece, E-mail: anagno@fluid.mech.ntua.gr

(Received January 27, 2012, Revised April 2, 2012)

A FAST LAGRANGIAN SIMULATION METHOD FOR FLOW ANALYSIS AND RUNNER DESIGN IN PELTON TURBINES*

ANAGNOSTOPOULOS John S., PAPANTONIS Dimitris E.

School of Mechanical Engineering, National Technical University of Athens, Greece, E-mail: anagno@fluid.mech.ntua.gr

(Received January 27, 2012, Revised April 2, 2012)

In the present work, an alternative numerical methodology is developed for a fast and effective simulation and analysis of the complex flow and energy conversion in Pelton impulse hydro turbines. The algorithm is based on the Lagrangian approach and the unsteady free-surface flow during the jet-bucket interaction is simulated by tracking the trajectories of representative fluid particles at very low computer cost. Modern regression tools are implemented in a new parameterization technique of the inner bucket surface. Key-feature of the model is the introduction of additional terms into the particle motion equations to account for various hydraulic losses and the flow spreading, which are regulated and evaluated with the aid of experimental data in a Laboratory Pelton turbine. The model is applied to study the jet-runner interaction in various operation conditions and then to perform numerical design optimization of the bucket shape, using a stochastic optimizer based on evolutionary algorithms. The obtained optimum runner attains remarkably higher hydraulic efficiency in the entire load range. Finally, a new small Pelton turbine (150 kW) is designed, manufactured and tested in the Laboratory, and its performance and efficiency verify the model predictions.

Pelton turbine, hydraulic efficiency, Lagrangian simulation, bucket shape parameterization, numerical design optimization

Introduction

Pelton hydraulic turbines are impulse type turbomachines commonly used in hydroelectric power plants with medium to high water head, as well as in various energy recovery applications (e.g., desalination units, etc.). One up to six spear valve injectors are used to direct high-velocity jets towards the inner surface of the rotating buckets mounted on the hub, where the kinetic energy of the flow is transformed to mechanical energy at the shaft. Since its invention by Lester Pelton and first configurations in the late 19th century, the bucket shape and the performance and efficiency of the runner have substantially improved, mainly based on the accumulated practical experience of manufacturers.

Recently there is a renewal interest towards a deeper understanding of the complex flow mechanisms evolving during the jet-bucket interaction in orderto access their impact on turbine performance and their contribution to the various hydraulic losses. Thanks to the continuous increase of computing power and to the development and application of advanced simulation methods and innovative experimental techniques, a complete design optimization of the buckets and of the distribution system may be achievable in the following years, maximizing the performance and cost-effectiveness of these machines.

Flow visualization techniques constitute useful diagnosis tools in Pelton turbines. Such studies identified the effects of distribution piping and injector design on the injected jet quality problems (unsteady and divergent behaviour, and surface disturbances). The importance of jet quality and its relationship with energy conversion efficiency in the turbine runner was thoroughly investigated[1].

Detailed measurements of the free-surface flow properties in the bucket are very difficult because of the contaminating effects of the water outflow. Direct measurements of the jet-bucket interaction concern mainly pressure distribution and water layer thickness in the inner surface of stationary buckets[2]and of ro-tating buckets[3,4]. The above studies indicated the need of further research to understand the role and quantify the effects of all participating flow mechanisms.

An extended flow mechanical analysis was made in Ref.[5,6] using a theoretical method to calculate the flow in a Pelton bucket. The jet impact work while entering the bucket, the effectiveness of all active forces in the bucket and the particular contribution of the flow friction forces to hydraulic efficiency have been quantified. An animated cartoon frames method was proposed and applied in Ref.[7] to discretize the unsteady jet-bucket interaction and predict the dynamic performance of the turbine.

The complete numerical simulation of the complex unsteady free-surface flow developed in a rotating bucket is a difficult computational task and a great challenge even for today’s computing power and CFD models. The Volume-of-Fluid method and the two-phase homogeneous or inhomogeneous models were implemented in various Eulerian solvers. Among the latest such studies are the works of Mack et al.[8], Zoppé et al.[2], Perrig et al.[3]and Santolin et al.[9], concerning from a stationary bucket to a complete single or multi-injector system and rotating runner including penstock and casing. CFD results can be used as input for the structural analysis of Pelton runners[10].

Lagrangian meshless simulation approaches provide some important advantages for the simulation of the flow during jet-runner interaction, such as the inherent simulation of the free surface flow pattern, and the capability of easily extending the calculations in the outflow from the bucket in order to the simulate of its interaction with the runner, jets, and casing. The Moving Particle Semi-implicit method[11]and the Smoothed Particle Hydrodynamics (SPH) method[12,13]are promising, however, their performance and accuracy are still not satisfactory, and further development and improvements are needed. A recent hybrid SPHALE approach[14]can help to overcome the main drawbacks of standard SPH method related to stability and accuracy.

Numerical analysis and optimization has been commonly used today in the design phase of all Pelton turbine components, and advanced software tools have been applied[15]. However, concerning the flow in the runner, although these computations can simulate the entire working cycle of the bucket, the accuracy of the torque predictions is still not adequate, mainly due to the development of complex secondary flows mentioned above that are not modelled[4]. Also, some uncertainties regarding the jet structure at the nozzle exit or behind the cutout region of the bucket, and some inaccuracies associated with the turbulence modeling cannot be avoided. Moreover, the traditional meshbased Eulerian approaches face significant numerical diffusion problems due to the complex evolution of the free surface flow pattern, whereas the unsteadiness of the flow requires extended and fine meshes with enormous computations, which are still not feasible for industrial design.

This work aims to present the main features and some application results of a new simulation tool that uses a Fast Lagrangian Simulation (FLS) method to provide reasonable energy conversion details during the jet-bucket interaction and to reproduce the runner performance characteristic curves at negligible computer cost[16]. A new parameterization method developed for the complex bucket shape is also described in detail and used during a numerical design optimization procedure of a Pelton turbine.

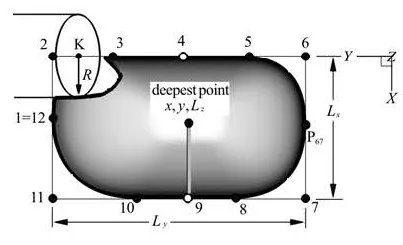
Fig.1 Design parameters and control points of the bucket rim

1. Numerical methodology

1.1 Bucket surface parameterization

The shape of the inner surface of a Pelton turbine bucket is represented using modern parameterization techniques based on the method of Non-Uniform Rational B-Splines (NURBS). The parameterization of the half symmetric bucket geometry is realized in two stages. In the first the rim geometry is defined using a closed Nurbs curve, as shown in Fig.1. The dimensionsxL andyL of the orthogonal frame containing the rim curve of the half symmetric part of the bucket are the main design parameters (see Fig.1). The rest control points are then properly placed on this frame to create the rim curvature, and they can be displaced along the x or y direction to deform its shape. Point 1 (or 12) and P67control the shape and the curvatures of the front and back sides, respectively, whereas Points 3, 5, 8, and 10 define the lateral sides of the rim. Points 4 and 9 are placed in the middle of Sections 3-5 and 8-10, respectively, to inactivate the restriction due to multiplicity of the latter points.

The notch cut section and the cutout lips are constructed at the intersection of the bucket surface with a cylindrical beam, which includes the water jet and is defined by two design variables representing its axis location and radius (see Fig.1). The third main dimen-sion of the bucket is its depth,zL, whereas two more variables determine the exact location of the deepest point in the -xy plane.

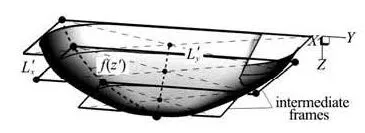
Fig.2 Parameterization of the lateral bucket surface

The second parameterization stage concerns the three-dimensional lateral surface of the bucket, which is assumed to consist of successive parallel slices, starting from the bucket rim plane and terminating at its bottom tip (see Fig.2). The shape of each such slice is defined by interpolation techniques between the first rim frame and a number of intermediate guiding frames distributed in thezL distance that determine the rate of change of the slice width and length (see Fig.2).

In order to reduce the number of free design variables, the following method is adopted to construct an intermediate frame. First, the intersection point of its diagonals is located on the same line connecting the corresponding point of the rim frame and the bucket deepest point (see Fig.2). Next, a distribution function of the frame dimensionsxL＇andyL＇along the z direction is defined with the aid of corresponding scaling factors. In case of one intermediate frame the function is parabolic

The coefficients a , b and c for each frame direction can be computed from three (z＇,f) pairs, the first of which is (0,1) and the last (1,0), whereas the third refers to the depth and size of an intermediate frame in this direction. Therefore, one intermediate frame introduces 3 additional design variables, whereas for two frames the distribution formula becomes cubic and 6 design variables are required. The distribution function must be a concave curve in order to maintain the required curvature of the bucket, whereas an additional constraint imposed is that the projection of all intermediate frames onto thex-y plane must be within the projection of the rim frame Lx-Ly. Finally, the Nurbs curves on the intermediate frames are constructed by interpolation, using the above distribution functions in the x and y directions and starting from the corresponding control points of the rim curve.

The advantage of the above technique is that the lateral bucket surface can be created using only 3 additional control points, allowing at the same time for large modifications of its shape, as will be shown later in this paper. Moreover, the produced surfaces are always smooth and without improper gradients or undesirable curvature variations. Overall, the construction or modification of the entire inner surface of the bucket can be controlled by a number of 19 free geometric variables, which is a quite small number for such complex three-dimensional shape.

One more parameter is introduced to control the radial location of the bucket, which ultimately determines the diameter of the runner (pitch radius), whereas the mounted angles of buckets can be also varied. Finally, some geometric constraints are imposed to maintain a minimum slope at the bucket’s splitter tip (here 10o), as well as at the outer tip (here 15o) in order to avoid impingement of the exiting flow on the backside of the next bucket.

1.2 Flow modeling

The numerical simulation of the fluid flow developed on the bucket surface is based on the Lagrangian approach, and the trajectories of an adequate number of representative fluid particles are tracked in order to produce statistically accurate results. The jet volume is divided into several consecutive segments or frames, and a number of particles are uniformly distributed over the circular area of each frame, as shown in Fig.3.

Fig.3 Initial distribution of representative flow particles

The jet-bucket interaction starts when at least one particle of a frame impinges on the bucket. That instant corresponds to a specific angular position of the bucket, which depends on its geometry, mounted angle and pitch radius, but also on the jet diameter and hence on the turbine load (flow rate) conditions. For the examined runner operating at its maximum load, this happens at an angle θ≈–39o, as defined in Fig.3. The calculations are then continued for the particles of the oncoming frames, until all particles of a frame impinge on the next coming bucket (jet cut).

The equations of motion of the fluid particles are solved in a rotating (with the runner) orthogonal system of reference, and are expressed as follows:

where x, y and z are the Cartesian coordinates as defined in Figs.1 and 2,ω is the angular rotation speed of the runner and fx, fyand fzare functions of the local surface geometrical characteristics.

The calculation of a particle trajectory is divided into two parts. First, the standard particle equations without the above f-functions are solved to reproduce the particle’s path in the free jet, and the algorithm checks only if the particle impinges on the next coming bucket in order to stop the integration. Otherwise, the tracking process continues until the particle encounters the inner bucket surface or passes through the cutout notch without meeting the runner. A third option is also possible in some off-design conditions, when a particle may not meet the runner at all (ineffective jet section).

Fig.4 Calculation of particle’s path on the surface

The particle tracking after impacting on the bucket surface is more complicated and can be explained with the aid of Fig.4. Assume that the particle does not rebound but rather slides along the surface, then the resulting velocity vector, V2, belongs to the plane defined by the impinging velocity, V1(u1,v1,w1), and the normal vector n to the surface at the impact point (for zero losses V2=V1). The particle velocity components after the impact, as also after any direction change along its pathway, are (see Fig.4)

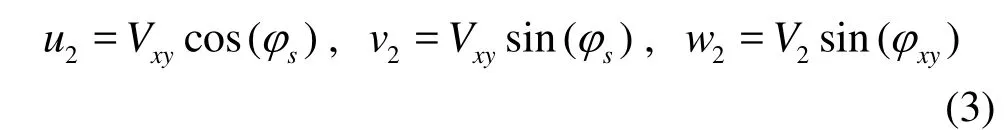
where Vxy=V2cos(φxy), and the angles φxy,φsare computed by vector calculus from the surface geometric data:

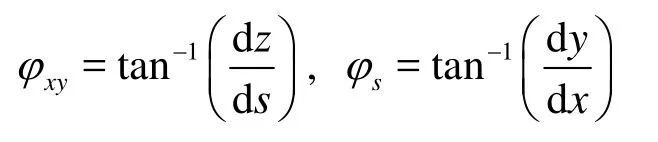
The above velocity components are then used to calculate the particle location along the x andy directions after the next time step, Δt:

whereas the third coordinate, znew, must be always on the bucket surface, hence it is computed by the surface parameterization algorithm.

The particle tracking after impacting on the bucket is performed by numerical integration of Eq.(2). A second-order predictor-corrector scheme is adopted for the step-by-step calculation of the trajectory and the procedure is repeated until the particle flows out from the bucket.

The above equations do not contain any particle interaction terms, or any mechanical losses terms, and hence they cannot reproduce the real flow picture in the bucket. For this reason, the present methodology introduces a number of additional terms in order to account for the hydraulic losses along the particle’s pathway, and for the free surface flow spreading rate in the bucket shown as follows:

(1) Friction losses

Through assuming a constant mean friction coefficient, the kinetic energy of a particle reduces by a factor analogous to the square of particle velocity and to the sliding distance, hence the new particle velocity after a time step tΔ becomes

wherefC is a friction-loss adjustable coefficient.

(2) Impact losses

Additional kinetic energy losses take place due to abrupt change of particle momentum at its impact point. The kinetic energy losses are taken analogous to the square of the normal to the surface particle velocity component, and this gives

where Ciis the impact-loss adjustable coefficient andφithe angle between the particle impingement velocity and the unit vector normal to the surface at the impact point (see Fig.4).

(3) Change direction

The progressive change of particle’s path direction (and momentum) as it slides along the curved bucket surface also causes minor energy losses, which can be modeled in a way similar to the impact losses term

wherepC is the adjustable coefficient and φΔ the angular change in the direction of the sliding particle during the time step . tΔ

(4) Flow spreading

The lack of pressure field computations makes impossible the reproduction of the jet spreading rate on the surface after its impact. In order to remedy this deficiency it is assumed that each particle acquires at the impact point an artificial “spreading” velocity component perpendicular to its impacting plane (VSin Fig.5) while its main velocity magnitude is correspondingly reduced to preserve kinetic energy. A theoretical approach for this effect cannot be derived, and for this reason multiple tests and evaluations of several different relations where carried out. The finally adopted scheme involves two more adjustable coefficients to compute the magnitude of the “spreading”velocity. The first quantifies the influence of the relative position of a particle in the jet (radial and angular locations in respect to the jet axis and to the splitter direction, respectively, as shown in Fig.5). The second coefficient is introduced to account for a possible effect of the initial jet diameter (or the spear valve opening) on its spreading rate after the impact.

Fig.5 Modeling of flow spreading on the bucket surface

The above terms allow also to take into account, in an implicit manner, some complex flow mechanisms and instabilities evolving in this flow type that cannot be otherwise simulated. But the performance of the FLS model and the reliability of its results depend on the appropriate tuning of the values of the involved coefficients, and this can be accomplished with the aid of experimental data or of numerical results obtained by a more accurate CFD solver.

A sufficiently small time step (2×10–5s) is used for the numerical integration of the particle motion equations in order to reduce the numerical error. A total number of the order of 103trajectories was found adequate to produce independent results for the overall hydraulic efficiency of the runner, whereas for the reproduction of the surface flow pattern more than 104trajectories were computed. Even in the latter case, the CPU time requirements are very small, just a few seconds in a modern personal computer.

1.3 Monitoring and post-processing of the results

The FLS model includes post-processing of the results in order to compute the turbine performance characteristics, such as the torque developed on the buckets and the hydraulic efficiency of the runner. Also, it can be used to calculate the local forces exerting on the bucket due to the change of fluid particles momentum, and hence to assess the local contributions to energy conversion. Snap-shots of the flow pattern at any instant are easily obtained, and can be used to produce animation in graphics software at very low computer cost.

The mechanical torque is computed from the following equation of conservation of angular momentum

where Quis the cumulative flow rate that enters each bucket and w the absolute tangential velocity component at corresponding radial distance r. The mean angular momentum at the inlet, after assuming a uniform jet velocity Vjet, becomes

where Rrunis the runner pitch radius. The mean angular momentum at the bucket outlet is computed by averaging the local fluid particle properties monitored there

where riand wiare respectively the radial distance and the absolute tangential velocity component of particle i at the moment when it flows out from the bucket rim, and N is the total number of fluid particles interacting with a single bucket. The hydraulic efficiency of the runner can then be obtained as the ratio of the developed mechanical power divided by the corresponding net hydraulic power at the inlet wwhheerree HHjjeettaanndd HH aarree tthhee hhyyddrraauulliicc hheeaadd ooff tthhee ddiisscchhaarrggeedd jjeett aanndd ooff tthhee ffllooww aatt tthhee iinnjjeeccttoorr iinnlleett,, rree--ssppeeccttiivveellyy,,ω is the rotation speed of the runner and Qthe nozzle flow rate. The velocity coefficientφ stands for the hydraulic losses in the spear valve, and it is usually between 0.95 and 0.99[17]. The value of 0.975 is taken for the present study. Also, it must be noticed that the runner flow rate Quin Eq.(8) may be less than Q for certain off-design operation conditions, when some particles do not meet the runner.

Fig.6 Laboratory Pelton turbine model

2. Model application and results

2.1 Adjustment of model coefficients

The values of the coefficients described in Section 1.2 are regulated with the aid of available experimental data in an 80 kW Pelton turbine model, which was designed and manufactured in the Laboratory (see Fig.6). Its main geometrical and operational properties were obtained from the corresponding quantities of a large-scale turbine (scale 6:1), which is installed at a hydroelectric power plant of the Greek Public Power Corporation.

The feeding system comprises two injectors with the nozzle diameter 0.036 m and maximum discharging jet diameter at vena contracta about 0.031 m. Water is supplied by a 220 kW 3-stage variable speed centrifugal pump and recycles through the 300 m3water tank of the Laboratory, while a 75 kW DC generator is used as electric brake (Fig.6). 22 cast iron buckets are bolted on the runner with a 0.4 m pitch diameter. The design operation point is 270.6 m3/h for 129,6 m net head, at 1 150 rpm, and overall attainable efficiency about 82%[18].

A complete set of measurements of turbine operation across the entire loading range (spear valve opening) is used for the regulation of model coefficients, as shown in Fig.7. Each set of experimental data represents a specific valve opening or a corresponding jet diameter, Rj, given in the legend (Rmaxis the maximum jet radius at fully open nozzle), and it was taken by varying the runner rotation speed. The efficiency in Fig.7 are presented as function of a dimensionless flow rate parameter Φ, defined as

and they are converted for comparison to the design speed of the runner. The experimental data for the overall turbine efficiency are obtained from the relation

where M, Q, H and ω are the four quantities measured on the Laboratory test rig. The hydraulic and the mechanical losses of the runner cannot be directly measured.

Consequently, in order to compare the FLS model output with the measurements, the hydraulic efficiency, ηh, of Eq.(11) is converted to overall efficiency by the relation

wheremη is the mechanical efficiency of the runner (shaft bearings losses), estimated to 97% for all operating points.

The best coefficient values are then obtained as follows. At first, the inner shape of the model turbine buckets is well approximated using the present parameterization methodology, and then the FLS model is applied to simulate the flow for a specific jet diameter (here 92%, Fig.7). The numerical results for this efficiency curve obtained from Eq.(14) are compared with the corresponding measurements given by Eq.(13). A general optimization software (see Section 2.4 below) is then used to minimize the cumulative squared error between them, considering as free variables the adjustable coefficients of the model. After convergence of the optimizer the resulting coefficient values that achieve the best fitting are adopted as optimal ones. Next, the FLS model with the above coefficients is applied to reproduce the efficiency curves for all the rest spear valve opening conditions and the results are compared with the corresponding measurements in Fig.7.

Fig.7 Comparison between measured and predicted turbine efficiency

Fig.8 Flow field evolution on the bucket surface

The agreement is quite good almost in the entire loading range of the turbine, and in most operation points the observed discrepancies do not exceed 3 percentage units. The differences are significant only for the smallest jet radius near the closing position of the injector (Rj=0.46Rmaxin Fig.7). In this case the measurements show a drastic efficiency reduction, most probably due to jet degradation effects that are common in such injector types (deviation from the axis, surface disturbances or other instabilities), but cannot be modeled. On the other hand, the measured maximum attainable efficiency becomes smaller as the spear valve approaches its fully open position, partly due to the increasing jet interference effects with the outflow and with the droplets rebounding from the casing, as also due to the increasing windage losses in a mistier environment. This trend can be observed also in the numerical results plotted in Fig.7, though at a smaller degree, because this time it represents only a reduction of jet-bucket interaction efficiency due to larger jet diameter.

2.2 Analysis of jet-bucket interaction

An example of flow analysis capabilities of the FLS model is illustrated in Fig.8. The construction of successive time history views can provide a more comprehensive and enlightening picture of the complex unsteady flow evolution in the runner. For the case presented in Fig.8 the jet-bucket interaction starts at an angular bucket position of – 39oin respect to the vertical direction, and the angle θΔ denotes the rotation of the runner after that time instant (see also Fig.3).

The jet-bucket interaction starts when the first particle trajectories impinge at relatively small angles on the notch cut at the front edge of the bucket (Fig.8(a)). The free surface flow produced afterwards is initially directed toward the bottom and the root of the bucket (Fig.8(b)) but soon begins to spread on theentire inner surface, as the incident angle of the jet increases (Figs.8(c), 8(d)). Between =θΔ15oand Δθ=35othe full jet impinges on the splitter line at almost normal impact angles while moving slightly towards the center of the bucket (Figs.8(b) to 8(d)). At about 20othe jet starts to interact with the next following bucket too (Fig.8(c)), which eventually cuts it completely (Fig.8(d)). At about that time the flow starts flowing out from the bucket side edges (Fig.8(d)), and the evacuation continues up to about Δθ=60o(Figs.8(e), 8(f)). Therefore, the complete jetbucket interaction phase lasts about 60oof runner rotation. During the last stages shown in Figs.8(e) and 8(f) the remaining part of the separated jet is reaching the bucket again towards the front edge, due to the bucket rotation and elevation. The reduced number of representative particles in the last part of the jet causes some scattering in the surface flow pattern of Figs.8(e) and 8(f). Finally, though not shown in Fig.8, after Δθ≈30oa small portion of the surface flow leaves the bucket from the cutout lips of the notch, as was observed by other researchers[3].

Fig.9 Effect of the rotation speed

2.3 Off-design operation

The numerical model with the regulated coefficients can be applied to simulate the flow and to produce realistic predictions of the runner performance at various operating conditions. The results illustrated in Fig.9 is an example of such a study, in which the hydraulic efficiency, along with the mechanical power and torque developed on the shaft, are calculated as a function of the runner rotation speed, for fully open nozzle and for a fixed flow rate that corresponds to point Φ=0.0124 indicated in Fig.7. The three characteristic curves exhibit the expected behavior: The torque increases at lower speeds and the power and efficiency maximize within the same speed range. The latter is between 1 100 rpm and 1 300 rpm and complies with the design rotation speed of the runner (1 150 rpm). Also, from the same diagram the runway speed of the turbine can be estimated to be about 1 800 rpm.

The torque acting on the runner during a single jet-bucket interaction is plotted in Fig.10 as a function of the runner angular position and for three different operating conditions. The corresponding curves can provide more detailed views of the energy exchange in the bucket. For fully open spear valve the interaction starts when the bucket is at an angular position of about –39o, but for smaller openings the jet diameter is reduced and the first impingement on the bucket happens somewhat later (about –30ofor Rj= 0.46Rmax). On the other hand, in case of reduced rotation speed of the runner (n=920rpmin Fig.10) the interaction terminates earlier, because its duration depends of the relative jet-bucket velocity, which in that case increases. Also, the amplitude of the pulsating torque variation can be associated with the stress acting on the bucket root and shaft. In the reduced speed case, for example, the maximum developing stresses will be considerably higher than at nominal speed, although the areas below the corresponding torque curves are similar (see Fig.10).

Fig.10 History curve of bucket torque

2.4 Numerical optimization of runner design

A general stochastic optimization software based on evolutionary algorithms is implemented for the numerical optimization of runner design. The EASY software has been developed and brought to market by the Laboratory of Thermal Turbomachinery, NTUA[19]. It has the advantage of easy introduction of any number of design variables, and it is suitable for complex non-linear and multi-parametric problems as the present one. The algorithm selects values of the free design parameters within prescribed ranges and searches automatically for the set that maximizes the cost function (here the hydraulic efficiency of the runner) using populations of candidate solutions. The passage from a population to the next one that contains improved solutions mimics the biological evolution of species generations[19]. The geometric constraints are incorporated exclusively by giving a penalty value to the corresponding cost function whenever an unacceptable surface design is encountered.

The geometric variables used for the parametricdesign of the bucket inner surface in Section 2.1 constitute the free parameters for optimization. The runner pitch diameter was also treated as a free parameter. At first, various combinations of the above design variables are tested with the optimization software, in order to assess the relative importance of each one, as well as to determine their reasonable variation ranges. It was found that the hydraulic efficiency of the runner depends more on its main bucket dimensions (length, width and depth), than on the exact shape of its rim or on the lateral surface pattern. However, due to the cost function discontinuities that are introduced by the geometric constraints, the final optimization has to be carried out for all design variables simultaneously. The multi-parametric application reduces the convergence rate of the algorithm and requires several hundred up to a few thousands evaluations for convergence. The creation of inexact evaluations using neural network techniques is an option of the software that was activated to accelerate the procedure. A typical convergence curve is given in Fig.11, showing that the efficiency is maximized after about 2 000 flow simulations of different bucket geometries with the FLS algorithm. Fortunately, the latter is very fast and the whole procedure can be completed in a couple of hours using a modern PC.

Fig.11 Optimizer convergence history

Fig.12 Shapes of the inner bucket surface tested during optimization

Initially the optimizer selects random values within the prescribed ranges of the free variables, and after several new generations of candidate solutions it progressively locates the regions where the cost function (turbine efficiency) takes large values. As a result, lots of different shapes can be created and numerically solved during the first optimization stages, as in the examples of Fig.12, whereas near convergence most of the examined shapes look similar and approach the final solution. Due to the stochastic nature of the operation there is no strict convergence criterion. The procedure is terminated when efficiency is not further increased within a predetermined number of consecutive evaluations.

Fig.13 Comparison of inner bucket shapes

Table 1 Comparison between runner geometric parameters

The dimensions and shape of the finally obtained optimum bucket are not much different from the standard design of the Laboratory model bucket. This was expected, because the model turbine operates with a fairly good overall efficiency (above 82%). The new bucket is about 10% longer, narrower, and deeper than the standard one (see Fig.13). A comparison between the main bucket dimensions is given also in Table 1, along with the pitch radius values. The optimum value of the latter is slightly greater (about 2%) than that in the model runner.

Fig.14 Predicted overall turbine efficiency at various load conditions

The efficiency of the optimum runner is compared with the numerically obtained corresponding efficiency of the standard design. The results for various load conditions are drawn and compared in Fig.14. At full load operation the optimum design achieves 81% overall efficiency, namely 3 percentage units more than the standard design (78%, also in Fig.7). The optimum runner appears to be more efficient at all load conditions, although its superiority becomes smaller at smaller loads. The latter can be attributed to the reducing importance of the main bucket dimensions as the jet becomes thinner.

Fig.15 Effect of bucket size

The FLS model can then be used to perform sensitivity studies of the bucket design parameters and dimensions, in order to assess their particular effect on the runner hydraulic efficiency and to achieve a more elaborate final design. As an example, the bucket size is varied by increasing or reducing its main dimensions (i.e., the length, width and depth) at the same degree, so the modified shapes remain similar to the initial one. The results for both the standard and the optimal bucket designs are plotted in Fig.15. The overall turbine efficiency remains almost constant or reduces slightly when a larger up to 25% bucket is used. However, below a certain size the efficiency starts to drop, because an increasing portion of the jet flow passes by the runner without impinging on its buckets. This limit is close to the actual bucket size for the standard design (see Fig.15), verifying that its dimensions are cost-effectively selected. On the other hand, the optimal bucket seems to perform satisfactorily down to a size of about -10%, revealing that its final dimensions could be reduced below the optimal ones without substantial efficiency reduction. This indicates that for practical applications multi-objective optimizations must be applied, in order to take into account other important manufacturing and cost factors in addition to hydraulic efficiency.

2.5 Practical application and validation

The above design procedure using the FLS model is applied in order to find the optimum bucket shape for a new 150 kW Pelton turbine, which is then constructed and tested in the Laboratory (see Fig.16), prior to on-site installation at a small hydroelectric plant in Greece. The turbine was designed for the net head 135 m and nominal flow rate 0.1 m3/s, 1 m3/s to operate at the nominal speed 1 000 rpm. It has two injectors and the runner pitch diameter is 0.45 m. The new turbine is in about the same scale with the existing laboratory model turbine (80 kW), and for this reason the FLS model coefficients were taken as regulated for the latter, in Section 2.1.

Fig.16 The new small Pelton turbine on the Lab test rig

Fig.17 Comparison between measured and predicted Pelton turbine efficiency

Figure 17 presents the efficiency results of the turbine with one injector in operation, for several spear valve openings. The off-design values of the flow rate parameter were obtained by varying the rotation speed of the runner. The agreement between the measurements and the corresponding predictions of the FLS model is quite good along the entire efficiency curves, and the same was observed also for smaller and larger openings of the spear valve. The deviation observed again at the smallest valve opening can be attributed to the jet quality degradation as discussed previously in Section 2.1.

The above results validate the reliability of the FLS model and are very encouraging for using it as design tool for impulse hydroturbines.

3. Conclusions

The basic features and capabilities of a new numerical tool developed for flow analysis and performance improvement of impulse hydraulic turbines are presented and discussed in this work. The FLS model is based on the Lagrangian approach and the computation of representative particle trajectories. A new technique is also applied for the parameterization of the runner design based on the Nurbs polynomials, which utilizes a relatively small number of control points to produce suitable and flexible bucket shapes.

The new model introduces additional adjustable terms in the particle motion equations to account for the hydraulic losses and for the spreading of the surface flow on the inner bucket surface. This has the disadvantage of requiring experimental or numerical data from other more accurate methods in order to be properly regulated for each application. On the other hand however, it provides the capability of taking into account the effects of any instabilities and other complex secondary mechanisms evolved during the jetbucket interaction, which are very difficult or even impossible to be modeled. The results from a first regulation of the model coefficients based on available measurements in a laboratory Pelton model turbine are satisfactory.

The FLS model can produce very fast and realistic flow field results, and provide detailed information about the hydraulic behavior of the bucket and the energy transfer during the jet-runner interaction. Parametric and sensitivity analysis of operation or design parameters can be also easily performed. Moreover, due to its minor computer cost the FLS is very suitable for multi-parametric and multi-objective design optimization studies, which would need numerous evaluations and require huge computational resources if other more accurate CFD methodologies were applied.

The first practical application of the new model in the design phase of a new small Pelton turbine is successful and the obtained performance and efficiency of the turbine is quite close to the predicted one. It must be noted though that the FLS results cannot provide accurate picture of the real flow field and the various complex flow mechanisms during the jetbucket interaction. Hence, the model can be more useful during the first design optimization stages in order to localize and reduce the variation range of the free design parameters. In this way, the costly CFD simulation tools may be applied only for the last elaborating stage, reducing thus significantly the overall computer cost.

Additional and more detailed experimental data will be acquired in the Laboratory in order to validate further the model results and the optimal designs obtained in the present study. Such data, along with the results of more accurate CFD tools, will be used for better definition and more elaborate tuning of the model coefficients in order to make it more representative of the real physical mechanisms and to improve its reliability and applicability.

Acknowledgment

The authors would like to thank Prof. Giannakoglou K. and his team for the provision of the EASY optimization software and their help in the Nurbs technique implementation.

[1] STAUBLI T., ABOTTSPON A. and WEIBEL P. et al. Jet quality and Pelton efficiency[C]. HYDRO 2009. Lyon, France, 2009, Paper 2.05

[2] ZOPPÉ B., PELLONE C. and MAITRE T. Flow analysis inside a Pelton turbine bucket[J]. Journal of Turbomachinery, 2006, 128(3): 500-511.

[3] PERRIG A., AVELLAN F. and KUENY J.-L. et al. Flow in a Pelton turbine bucket: Numerical and experimental investigations[J]. Journal of Fluids Engineering, 2006, 128(2): 350-358.

[4] PERRIG A. Hydrodynamics of the free surface flow in Pelton turbine buckets[D]. Ph. D. Thesis, Lausanne, Switzerland: École Polytechnique Fédérale de Lausanne, 2007.

[5] ZHANG Z. Inlet flow conditions and the jet impact work in a Pelton turbin[J]. Proceedings of the IMechE, Part A: Journal of Power and Energy, 2009, 223(5): 589-596.

[6] ZHANG Z. Analytical method for frictional flow in a Pelton turbine[J]. Proceedings of the IMechE, Part A: Journal of Power and Energy, 2009, 223(5): 597-608.

[7] XIAO Ye-xiang, HAN Feng-qin and ZHOU Jing-lin et al. Numerical prediction of dynamic performance of Pelton turbine[J]. Journal of Hydrodynamics, Ser. B, 2007, 19(3): 356-364.

[8] MACK R., ROHNE W. and RIEMANN S. et al. Using the potential of CFD for Pelton turbine development[C]. 23rd IAHR Symposium on Hydraulic Machinery and Systems. Yokohama, Japan, 2006.

[9] SANTOLIN A., CAVAZZINI G. and ARDIZZON G. et al. Numerical investigation of the interaction between jet and bucket in a Pelton turbine[J]. Proceedings of the IMechE, Part A: Journal of Power and Energy, 2009, 223(5): 721-728.

[10] SICK M., MICHLER W. and WEISS T. et al. Recent developments in the dynamic analysis of water turbines[J]. Proceedings of the IMechE, Part A: Journal of Power and Energy, 2009, 223(5): 415-427.

[11] NAKANISHI Y., FUJII T. and MORINAKA M. et al. Numerical simulation of the flow in a Pelton bucket by a particle method[C]. 23rd IAHR Symposium on Hydraulic Machinery and Systems. Yokohama, Japan, 2006.

[12] MARONGIU J.-C., LEBOEUF F. and PARKINSON E. Numerical simulation of the flow in a Pelton turbine using the meshless method smoothed particle hydrodynamics: A new simple solid boundary treatment[J]. Proceedings of the IMechE, Part A: Journal of Power and Energy, 2007, 221(6): 849-856.

[13] KOUKOUVINIS P., ANAGNOSTOPOULOS J. and PAPANTONIS D. Flow modelling in the injector of a Pelton turbine[C]. 4th International SPHERIC Workshop. Nantes, France, 2009.

[14] MARONGIU J.-Ch., LEBOEUF F. and CARO J. et al. Free surface flows simulations in Pelton turbines using an hybrid SPH-ALE method[J]. Journal of Hydraulic Research, 2010, 48(Suppl. 1): 40-49.

[15] PARKINSON E., ANGEHRN R. and WEISS T. Modern design engineering applied to Pelton runners[J]. International Journal of Hydropower and Dams, 2007, 14(4): 91-95.

[16] ANAGNOSTOPOULOS J., PAPANTONIS D. A Numerical methodology for design optimization of Pelton turbine runners[C]. HYDRO 2006, International Conference. Porto Carras, Greece, 2006.

[17] NECHLEBA M. Hydraulic turbines-Their design and equipment[M]. Prague, Czech: Artia, 1958.

[18] ANAGNOSTOPOULOS J., PAPANTONIS D. Experimental and numerical studies on runner design of Pelton turbines[C]. HIDROENERGIA International Conference. Crieff, Scotland, UK, 2006.

[19] KARAKASIS M., GIANNAKOGLOU K. C. On the use of metamodel-assisted multi-objective evolutionary algorithms[J]. Engineering Optimization, 2006, 38(8): 941-957.

10.1016/S1001-6058(11)60321-1

* Biography: ANAGNOSTOPOULOS John S. (1962-), Male, Ph. D., Associate Professor