自动跟踪太阳能的成本优化

刘 阳，程宗毛

(杭州电子科技大学 理学院，浙江 杭州 310018)

在传统能源紧缺的今天，新能源和可再生能源的利用越来越受各国政府的重视.太阳能以其取之不尽、用之不竭、绿色环保、自由公平的特点成为人们瞩目的焦点.太阳是一个巨大、久远、无尽的能量源.尽管太阳辐射到地球大气层的能量仅为其总辐射能量(约为3.75×1026W)的二十二亿分之一，但已高达17 300 0 TW，也就是说太阳每秒钟照射到地球上的能量就相当于燃烧500万吨煤所释放的能量[1-2].太阳能的利用已成为21世纪重大的研究课题之一.在中国，太阳能资源是比较丰富的，从其地域分布来看，西部地区的太阳能年辐射总量均在5 400 MJ/m2以上，尤其是西藏地区，达到6 700 MJ/m2以上[3].开发好太阳能，对建设和谐社会有着重要的现实意义.本文主要从太阳能的追踪和成本优化两个方面进行描述.

1 太阳能跟踪问题

现有一平面 α.平面 α中心有一垂杆EO，平面 α内存在相互垂直的两根轴AB，CD(其中AB轴位于南北地轴与重力垂线组成的平面内)，平面 α均可绕AB、CD两轴自由转动.假定平面 α初始状态为水平位置，绕 AB 轴转动角度 θ的范围为(-150°，150°)，绕 CD 轴转动角度 φ 的范围为(-150°，150°).假设保持中杆顶点 E在平面 α的影子与 α平面几何中心 O始终重合.

这样，为了对太阳能跟踪进行比较好的分析，需要解决如下两个问题:

(1)计算出一年内任意一天日出时间和日落时间.

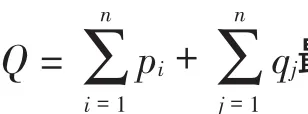
2 太阳能跟踪模型

为了使问题简化，现做以下假设:

(1)同一天内只考虑地球的自转影响，忽略公转;不同天内考虑公转;

(2)地球为严格的球体;

(3)地球公转轨道为严格的圆形轨迹，太阳为圆心;

(4)a-黄赤交角为23°26'，b-以杭州为例的地理纬度为北纬30°16'，c-任意时刻光线与水平面的交角;

(5)重力线指向圆心.

2.1 太阳能电池板的跟踪问题

首先，建立模型求解任意一天日出时间和日落时间.由于当阳光垂直入射面入射时，表面吸收太阳能最多.上述装置的要求正是基于这一原理[4-7].同时由于黄赤交角(23°26')的存在，地球公转产生四季变化建立在黄赤交角存在的基础上，地球自转产生昼夜交替，二者在同时进行着.地球的自转和公转导致地球上同一地点不同时刻以及每天的同一时刻，太阳入射角均不同，这样，之前所说的任意一天日出时间和日落时间也就不同.

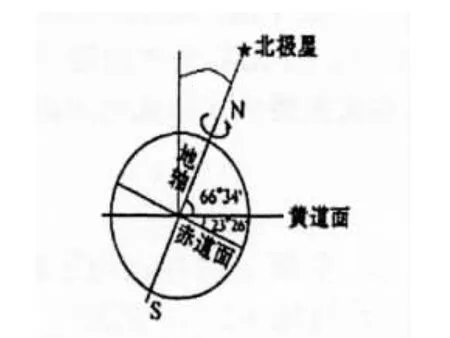
图2 黄赤交角示意图

黄赤交角的存在(见图2)，使太阳直射点到达的最北界线是23°26'N，即北回归线;最南界线到23°26'S，即南回归线，也就是太阳直射点在23°26'S～23°26'N范围内做周年往返运动.因此地表获得热量随时间和空间发生变化.

本文选取杭州进行分析.杭州(北纬30°16'，东经120°12')在北回归线以北，不会产生阳光直射地表现象，但可以通过调节倾斜面的倾角使之始终与光线垂直[8].

这样就得到了计算任意地方在任意一天昼夜长短、日出日落时间的通式:

假设某天太阳直射点的纬度为 δ1度(δ1在+23.5到-23.5之间)，观察者所处的纬度为 δ2度(δ2在+90到-90之间)，那么这天 δ2度地点的夜长为:

(说明:如果人在北半球，太阳在南半球，则 δ1应该取负值，那么结果也是负值，该值表示的是北半球那人所看到的昼长.)

所以，当地时间的日出时间为:

当地时间的日落时间为:

因为杭州位于东8区，与北京同一个时区，所以无需进行时间转换.

根据上述公式，例如，要计算杭州在夏至这一天的日出时间，已知杭州在北纬30°16'，即 δ2=30.27，夏至这天太阳直射北纬23.5°，即 δ1=23.5，把 δ1和 δ2的值代入(1)式，可计算出这天杭州的日出时间为5.02时，即5:01:12.查全国各地日出时间表得，杭州在夏至(6月22日)这一天的日出时间为4:58，误差约为3 min，误差较少.

接下来，建立模型求解一年内任意一天太阳直射点的纬度.设任意一天的日期为月日，当日期在夏至(6月22日)和冬至(12月22日)之间，即6月22日≤X，Y≤12月22日时:

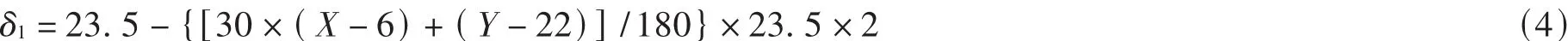
当日期在夏至(6月22日)之前，即时:

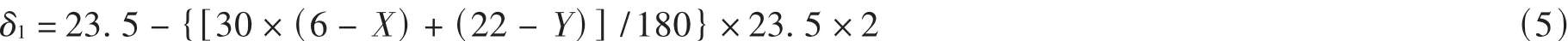
当日期在冬至(12月22日)之后，即时:

至此，杭州在一年内任意一天的最早和日落时间的计算模型已经建立.计算过程如下:假设任意一天为 X月Y日，先由(4)-(6)式计算该日太阳直射点纬度 δ1，然后将 δ1的值和 δ2的值(此处 δ2=30.27)代入(2)-(3)式即可求出 t1、t2.

2.2 太阳能最大获取模型

为尽可能多的在一年内获取太阳能，需要建立模型分析，通过求出机构的数目 n，选定合理的排列方式，从而给出一年内太阳总能量与总成本的关系.显然，要想最大限度的获取太阳能，只有将整个区域都布满 α平面机构，即当阳光直射该区域时，α平面机构平铺于该区域的各个角落且布满.但是这样布置，在其余大部分时刻(非直射时)将造成平面的相互遮挡，造成资源的浪费和总成本的增加.

设每个机构支撑面的边长为 b，则0≤b≤l，借助取下整函数来构造总成本关于每个机构支撑面边长的函数:

于是，得到了在有限区域 L×L内第 i天内获取的太阳总能量函数为:

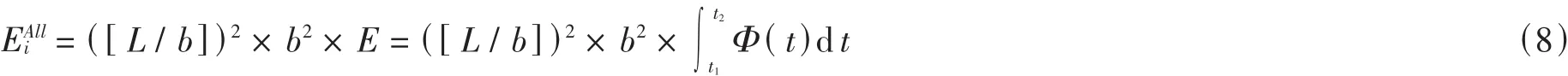
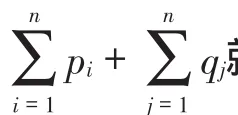
所以，区域 L×L内平面 α的排列方式为均匀平铺，每个机构的面积为 l×l.因此，求得机构总数目n=k2.这样，最小总成本就可以按照如下公式给出:

因为区域 L×L内平面 α的排列方式为均匀平铺，按这样的排列，由于遮挡因素的影响，平面上的不同位置虽然起始照射时间和最终照射时间不同，但是它们总的照射时间是大体相同的，约为当日日落时间与日出时间差值的一半(考虑 k＞＞1的情况，这样可忽略区域边缘两列特殊机构的情况).

上述论断可以通过演示加以粗略证明，这里不再详述.所以，第 i天内该区域 L×L内接受的总太阳能约为:

结合公式(7)和(8)，可以推出总成本 Q与第 i天内获取的总能量EiAll满足下列公式:

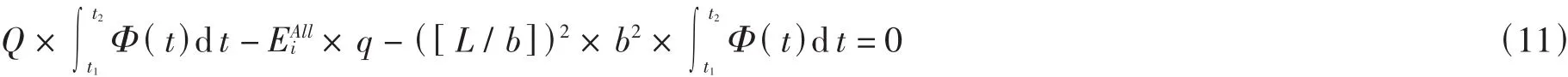
需要求的是一年内获取的总能量，所以，对 i求和即可，得到以下公式:

编写Matlab程序求解，得到了一年内太阳总能量与总成本关系的图像，如图 3所示:

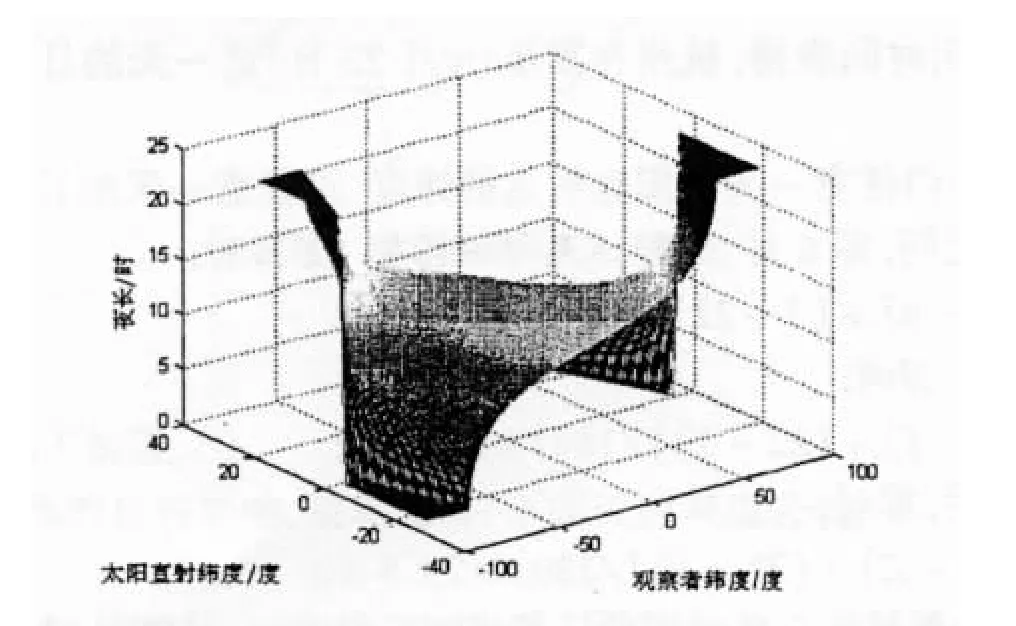
图3 太阳总能量与总成本关系

3 展望

本文提出一种自动跟踪太阳能装置的成本优化，得到在成本一定的情况下一年内太阳总能量与总成本的关系.但是，并没有分析研究获取的总能量与成本的关系，这些是可以进一步分析讨论的.

[1]姚伟.太阳能利用与可持续发展[J].中国能源，2005，27(2):46-47.

[2]杨帆，杨景常，郑宇.向日葵型跟踪太阳智能发电装置的研制[J].西华大学学报，2007，26(6):18-20.

[3]李锦堂.20世纪太阳能科技发展的回顾与展望[J].太阳能学报，1999，特刊.

[4]郑小年，黄巧燕.太阳能跟踪方法及应用[J].能源技术，2003，24(4):149-151.

[5]陈维，李戬洪.太阳能利用中的跟踪控制方式的研究[J].能源工程，2003(3):18-21.

[6]张兴磊，杨丽丽，张东凤.一种太阳自动跟踪系统的设计[J].青岛农业大学学报:自然科学版，2008，26(4):315-318.

[7]袁志国，阙沛文，黄作英.一种太阳跟踪装置的设计[J].自动化与仪表，2007(2):30-33.

[8]王炳忠，汤洁.几种太阳位置计算方法的比较研究[J].太阳能学报，2001，22(4):413-416.