一种新型直流永磁球形电机位置检测方法的研究

李丹，凌有铸，方愿捷，陈秀琴

（1.安徽工程大学 安徽省电气传动与控制重点实验室，安徽 芜湖 241001；2.天津电气传动设计研究所，天津 300180）

1 引言

近年来，球形电机的研究受到了广泛的重视，究其原因在于它独特的球形结构可以在一定范围内的任意点处进行定位与控制。本文在分析多自由度电机发展现状与趋势的基础上，针对直流永磁球形电机位置检测进行了相关的分析和研究。

2 球形电机位置检测研究的发展现状

美国佐治亚大学在研究球电机方面取得了卓有成效的成就［1-2］。他们对基于步进和变磁阻原理的球形电机转子的位置检测，是采用一套滑轨支架测量系统来实现的。其检测原理为在与转子相连的滑轨支架上安装了3个独立的增量式旋转编码器，利用这3个编码器来获取转子的相关位置信息，并通过一些运动学分析，得出相应的求解方法。虽然这种球电机的工作空间较大，但仍存在如下问题：一是位置检测机构不理想，如图1所示的滑动导轨不仅外形庞大，而且在运动中的摩擦力也较大，给驱动力矩增添了很大负担；二是转子和定子间的支撑方式不理想。这里，转子是通过几个滚珠轴承和定子相连接的。由于转子和定子间的摩擦力很大，运行一段时间后，机械磨损造成的位置精度下降是个严重的问题。

图1 滑轨支架测量系统Fig.1 Slide bracket detection system

最近几年，国内有关研究人员对永磁球形电机的位置检测进行了大量系统的研究［3-5］。针对电机转子的位置检测，采取了在转子球面上按随机编码规则确定黑、白两种颜色，采用光电传感器对转子上的颜色进行识别，并由此推理计算出转子当前所处的空间位置。求解的过程归结为对状态空间的搜索，其搜索策略是要解决组合爆炸的问题、建立评价函数进行启发式搜索。可见，现有的位置检测方法几乎都是通过大量的枚举或者大量位置数据的搜索来寻优。

在球电机的位置检测过程中，其三维位置检测的困难在于无法像一维那样存在实际的、可以看得见摸得着的旋转轴，虽然三维旋转在空间上事实地存在3根正交的旋转轴，但这个轴无法实际的提取到。因此上述这类方法对实时控制和检测精度都不可能是理想的。而本文提出的一种被动3自由度球关节的设计方法，可以把这3根正交的旋转轴提取出来，使三维位置检测就像一维那么简单和方便。

3 对转子位置的检测方法

3.1 概述

本文所研究的直流永磁球形电动机如图2所示，它是由新加坡南洋理工大学主持开发的直流永磁3－DOF球电机样机［6］。

图2 NTU－SIM Tech球电机Fig.2 NTU－SIM Tech spherical motor

依据样机进行分析，并重新设计加以改进，为了有效减小转子和定子的机械摩擦，本设计的球电机选用图3所示的被动球轴承来有效解决转子和定子间的摩擦问题，并结合3自由度位置检测的需要，研制了被动3自由度球关节来解决机械摩擦问题。图3a是它的内部结构，由于旋转部分是钢珠滚动的，因此摩擦力很小，可以长期使用。

图3 定子和转子的机械结构Fig.3 The mechanical structure of the stator and rotor

在位置检测上，采用在球轴承顶端平面放置双轴倾角传感器，在球关节底部旋转轴放置旋转编码器来检测相应信息的方法解决转子的位置检测问题。

3.2 球形电机位置检测的系统模型

本文所使用的双轴倾角传感器检测出的是正常水平时的双轴（如图4a中X，Y）与倾斜后的双轴（如图4b中X′，Y′）的夹角度数。记X′与X 之间夹角为α，Y′与Y之间夹角为β。记旋转编码器检测出的角度为γ。

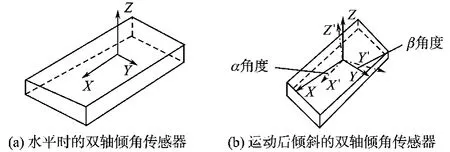
图4 双轴倾角传感器模型Fig.4 The model of dual－axis tilt sensor

要实现对转子的位置检测，就必须对球面上的点进行定位，而对球面的分割则是关键。考虑到检测的对象是一个空间位置相对固定的标准球体，借鉴地理测绘学中“大地坐标系”这一概念［7］，在传统的x，y，z三维空间坐标系中建立一个球面的经纬度坐标系，球面坐标系的位置与半径大小，和转子的位置与半径大小相同，故两球面重合（为了方便观察，绘图时将经纬坐标系半径略大于转子半径），球面上的点用经纬度二维坐标表示，这时球面上某一点运动后的位置，可仅用一组二维坐标表示。这种方法可以成功地将双轴倾角传感器和旋转编码器检测到的α，β，γ三维数据通过一定的计算，转化为经纬度坐标的二维数据，最后再将其换算成传统的x，y，z三维空间坐标，以利于进一步的电机控制运算［8-9］。这样不仅可以较好地解决球面定位的问题，还可以简化繁琐的高维矩阵计算问题，有利于DSP进行一系列的计算，加快数据的处理速度，提高检测的实时性。

3.3 转子检测经纬度坐标系的建立

参照地球大地坐标系的建立方法建立的转子经纬度球面坐标系如图5所示。

图5 转子位置检测经纬度坐标系的建立Fig.5 Rotor of position detection to establish the coordinate system

建立方法：将球面坐标系的球心与x，y，z三维空间坐标系的原点重合。球面坐标系北极（北纬90°）对应转子轴所在的位置，x轴过0°经线所在的球割面，并与割面半径重合。y轴过东经90°所在球割面，并与其割面半径重合。

经度的建立：将经度坐标用L表示。它以0°经线为基准，向东西方向算至该点子午线作为该点的经度，由0°到180°计量。0°经线向东计量的叫东经，缀以“E”；向西计量的叫西经，缀以“W”，如30°W。

纬度的建立：将纬度坐标用B表示。它以赤道面（0°纬线）为基准，向北（Z轴正方向）或向南（Z轴负方向），由0°到90°计量。由赤道面向北（Z轴正方向）计量的叫北纬，缀以“N”；向南（Z轴负方向）计量的叫南纬，缀以“S”，如30°S。为了便于计算，须将E，W，N，S等地理记法设为数学的正负号，如表1所示。

表1 地理记法的符号转换Tab.1 Symbol conversion of geographic notation

3.4 转子位置检测的算法实现

先将α，β，γ坐标转化为经纬度坐标。

如图5所示，设转子轴位于北极点时为初始位置。根据设计的电机结构，转子永磁体是位于球面赤道上，共8个，每个永磁体之间相隔45°。为了便于分析计算，将其中1个永磁体A的位置置于经度0°，那么，该永磁体的LB坐标就为（0，0），当转子运动时，转子内部球关节中的双轴倾角传感器和旋转编码器便会测出3个角度数据，按照3.2节中的记法，分别将其记为α，β，γ。其中γ角以从北极方向看去的逆时针旋转方向为正方向。

通过计算可知，将倾角α，β，γ换算成该点的LB坐标系统的换算式为

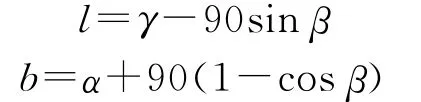
将LB坐标系统换算成x，y，z坐标系统的换算式为

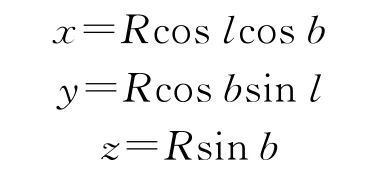
由此可以得出初始位置在（0，0）点的转子运动后所处位置的三维坐标。

3.5 转子上其他任意点的位置检测

由3.4节已经可以得出起点在LB坐标（0，0）处的永磁体运动后的位置，设运动到新位置后，该永磁体的坐标为ri（xi，yi，zi），另一永磁体B 点的坐标为rj（xj，yj，zj），c（o1，o2，o3）为转子上的固定的某一点位置。AC，BC之间的距离公式表示如下：

根据球形电机的运动控制原理，某2个定子线圈通电后产生磁场，即可吸引定子上的永磁体产生转动。假定线圈A′，B′组合而成的线圈满足运动控制需要的通电条件，设线圈A′点的坐标为sm（xm，ym，zm）、线圈 B′点的坐标为sn（xn，yn，zn），C′点为转子运动后A，B点分别运动到A′，B′点时，C点所处的位置。根据电机的结构和运动控制方案，A，B点之间的距离和A′，B′点之间的距离是相等的。

由电机设计可知，A，B和C 点是在转子表面，A′，B′是在定子表面，并且忽略转定子间的空气间隙，假定转子和定子半径相等，因此，它们的各点坐标均在以下集合中：

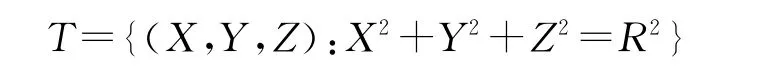
式中：R为球体半径。

因为C′是C点旋转后的位置，显然它也在集合T内。

根据下式：

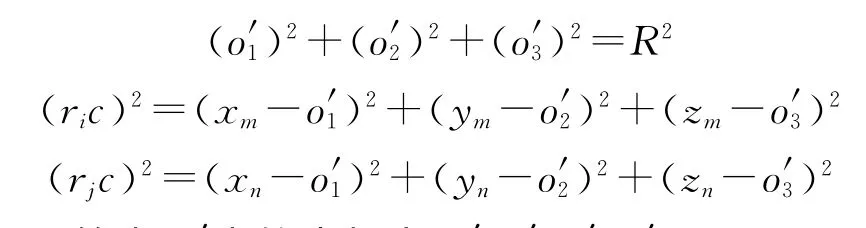
即可算出C′点的坐标为C′（o′1，o′2，o′3）

由此可知，只要转子永磁体的相对位置固定不变，球体上任意点的位置均可测出。

4 系统硬件组成

由于球形电机本身存在运动实时性高、方向多样化等不确定因素较多，故对控制系统的精度、速度均有较高的要求。本系统的控制器是以TMS320LF2407ADSP为核心，根据双轴倾角传感器和旋转编码器输出的球关节三维倾角数据，综合处理成位置检测信号，最终可算出球形电机转子上某一点运动前后所处的位置坐标。

本系统采用的双轴倾角传感器采用2只360°／S陀螺传感器与双轴倾角传感器结合，可以实现快速倾角功能，测量范围可达±90°，以TTL232方式与上位机进行通讯。

旋转编码器采用规格为1 000脉冲／r的增量型光电式旋转编码器，采用A，B两相输出，用以测量旋转角度［10 11］。

显示模块采用LCD1602字符型液晶显示模块，16脚（带背光）接口，显示容量为16×2个字符。

在考虑芯片电平连接时，因采用的双轴倾角传感器为TTL电平方式，故其RXD，TXD可直接与DSP2407的SCI异步串行发送引脚（SCITXD）和SCI异步串行接受引脚（SCIRXD）相连。LCD1602字符型液晶显示模块的电压为＋5V，而DSP2407的I／O口输出电压为3.3V，故需要电平移位器74LVC4245从中来进行电平转换，具体连线如图6所示。

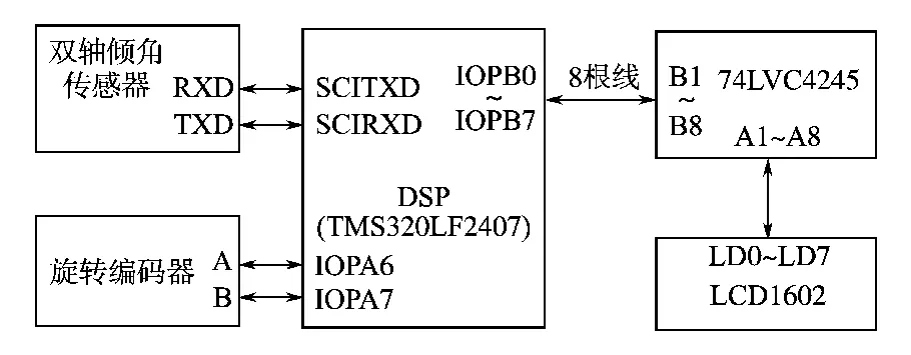
图6 位置检测系统硬件基本框图Fig.6 Basic block diagram of the position system hardware

5 运算实例

按照上文的位置检测算法，用VC＋＋6.0开发系统编译出了运算人机界面，如图7所示，在左框内输入双轴倾角传感器和旋转编码器实时输出的α，β，γ值，即可直接显示出初始位置在（0，0）点的永磁体运动后的x，y，z坐标值。例如，用以下几组数据做实验，设R＝1，运算结果如表2所示，运用Matlab进行仿真，坐标和转换计算器界面如图8所示。将仿真结果与真实球体三维倾斜实验后的结果进行对照可知，该方法测出的点的位置是准确的。

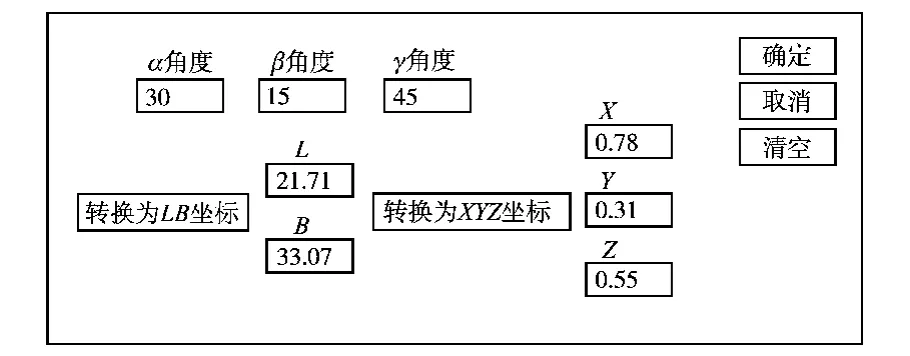
图7 坐标和转换计算器界面Fig.7 Interface of the coordinate conversion

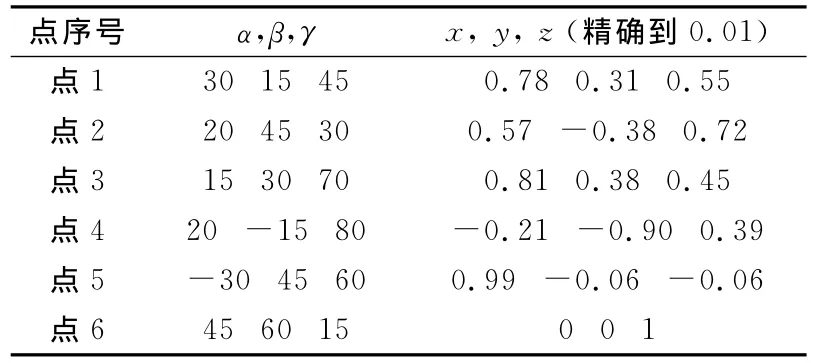
表2 计算得出的数值Tab.2 The data of the calculated

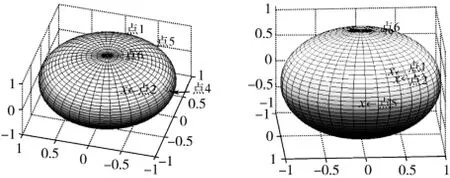
图8 仿真结果Fig.8 Simulation results

6 结论

直流永磁球形电机作为一种全新理念的电机，具有多种传统电机无法比拟的优点，但是由于其结构和运动方式的特殊性，导致其转子位置检测方法不同于传统的单自由度旋转的电机，关于此问题的研究，国内外还处于初步的探索阶段。本文以TMS320LF2407ADSP为核心，搭建软硬件检测平台，深入分析和研究3自由度球电机的基本工作原理，针对球电机的三维位置检测的困难，提出了一种被动3自由度球关节的设计方法，从而可以有效地解决球电机的位置检测问题。

［1］Lee K M，Pei J.Kinematic Analysis of a Three Degree－offreedom Spherical Wrist Actuator［C］∥Advanced Robotics Fifth International Conference，1991，1：72－77.

［2］Lee K M，Kwan C K.Design Concept Development of a Spherical Stepper for Robotic Applications［J］.IEEE Transactions on Robotics and Automation，1991，7（1）：175－181.

［3］王群京，雍爱霞，陈丽霞，等.一种永磁球形步进电机转子位置的检测方法［J］.中国电机工程学报，2006，26（22）：92－96.

［4］雍爱霞.一种简单高效的永磁球形步进电机位置检测的方法［J］.微电机，2010，43（9）：85－88.

［5］过希文，王群京，李国丽.多自由度永磁球形电动机控制策略的研究与发展［J］.微特电机，2011，39（2）：72－76.

［6］Yan Liang，Chen I－Ming，Lee K M，et al.Empirical Formulation of Torque Output for Spherical Actuators with Low－cost Rotor Poles［C］∥IEEE／ASME International Conference on Advanced Intelligent Mechatronics，2009，1：1625－1630.

［7］朱华统，杨元喜，吕志平.GPS坐标系统的变换［M］.北京：测绘出版社，1994.

［8］Yan Liang，Chen I－Ming，Son Hungsun，et al.Analysis of Pole Configurations of Permanent－magnet Spherical Actuators［J］.IEEE／ASME Transactions on Mechatronics，2010，15（6）：985－989.

［9］Zhang Liang，Yan Liang，Chen Weihai，et al.Current Optimization of 3－DOF Permanent Magnet Spherical Motor［C］∥IEEE Conference on Industrial Electronics and Applications，2011，6：1111－1116.

［10］赵仁德，曲华龙.电机的定点DSP控制中转速测量新方法［J］.电气传动，2010，40（6）：72－74.

［11］张涛，杨振强，王晓旭.应用eQEP及编码器测量电机位置与速度的方法［J］.电气传动，2011，41（4）：48－51.