冷轧机压下系统无模型控制器的设计与仿真分析

王宏文，高维国，王艺伶，黄巍巍

（河北工业大学 控制科学与工程学院，天津 300130）

1 引言

板带冷轧位置自动控制（APC）是厚度自动控制（AGC）系统的重要组成部分，往往作为轧制控制策略的内环，使系统快速消除外来因素对预设辊缝的影响，实现恒辊缝控制。冷轧机压下系统是APC的执行机构，一般采用PID控制，其响应的快速性和调节精度在很大程度上会影响轧后带材的纵向厚度精度。

板带材冷轧生产过程连续性强，现场干扰因素众多，具有高阶非线性、大滞后、不确定等特点［1］。传统的控制方法包括模糊自适应PID控制，都局限于参数最优，无法实现控制器结构的自适应最优控制。

为此，本文针对液压压下系统的特点，将各部件进行建模，利用现场参数得到具体的数学模型，将无模型自适应控制（model－free adaptive control，MFAC）思想应用于电－液伺服驱动的冷轧机压下系统的控制中，以提高轧辊位置控制的抗干扰能力和控制精度，进而提高板带材厚度精度。无模型自适应算法是一种既有现代控制理论与经典PID理论的优点，又能适应复杂系统优化控制要求的算法［2］。仿真结果表明了无模型自适应控制器能够适用于高阶非线性、大时滞、不确定的被控对象。

2 冷轧机压下系统建模分析

河北省某钢厂采用单机架可逆冷轧机，钢坯以厚度为3～4mm的碳素钢为主，轧制3个道次，轧后成品为0.12mm薄钢带，控制系统采用欧姆龙CS1系列PLC，采用位置、厚度双闭环控制策略，原位置环控制采用模糊PID算法。为进一步提高轧辊位置精度，钢厂进行工艺改造工程，首先对现场设备及新的控制策略采取了建模与仿真分析，以检验改造方案的可行性。

位置环控制由液压压下位置伺服机构完成，其主要由MFA控制器、伺服阀、液压缸和辊系负载构成，如图1所示。

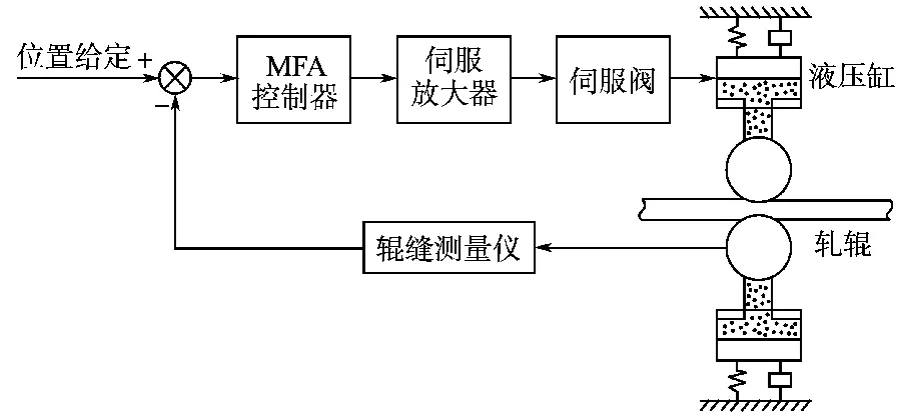
图1 压下系统位置伺服机构框图Fig.1 Block diagram of position servo system for screw down system

2.1 伺服放大器

伺服放大器起放大作用，故将此机构视为纯比例放大环节，传递函数设为

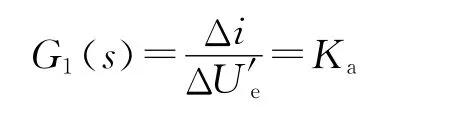
2.2 伺服阀

伺服阀的数学模型要根据其在系统中的使用情况具体决定，轧制现场采用的是MOOG760系列2级伺服阀，灵敏度高，动态响应快，固有频率大于50Hz，故此伺服阀的传递函数按2阶振荡环节处理［3］。

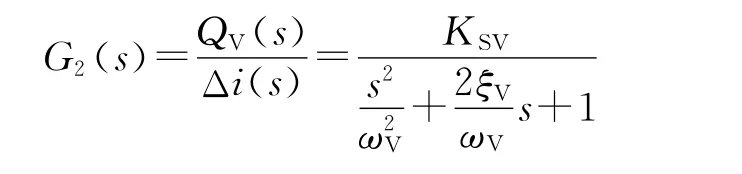
式中：ξV为伺服阀的阻尼系数；KSV为伺服阀的增益；ωV为伺服阀的固有角频率。

2.3 压下油缸及辊系负载

根据液压缸流量平衡公式，并由分布参数模型［4］，将上支撑辊与上工作辊作为一个质量体系，下支撑辊与下工作辊作为另一个质量体系，将轧机机架简化为两自由度弹簧阻尼系统，按照液压伺服控制原理得出在位置控制方式下液压缸及辊系负载的传递函数：

其中

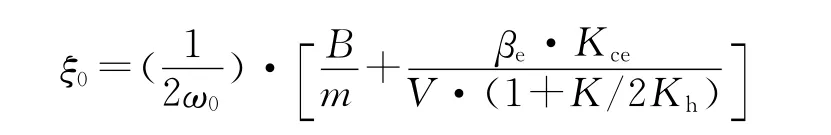
式中：Kce为总流量压力系数，Kce＝KC＋K1，KC为伺服阀流量压力系数，K1为油缸泄露系数；A为液压缸无杆腔的有效面积；K为轧机等效负载刚度；ωr为惯性环节角频率，ωr＝KKce／A2（2＋K／Kh），Kh为油液弹簧刚度，Kh＝βeA2／V，βe为液压油体积弹性模数，V 为液压缸前腔体积；ω0为振荡环节无阻尼自由振荡频率；ξ0为振荡环节阻尼比。

2.4 辊缝测量仪

辊缝仪作为位置传感器，可视为比例环节，传递函数为

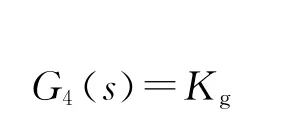
3 基于MFAC的控制器设计

3.1 无模型自适应算法

无模型自适应控制是一种无需建立过程模型的自适应控制方法，既不是基于模型也不是基于规则［5］，而是一种基于信息的全新的控制方法。

对于离散时间非线性系统：

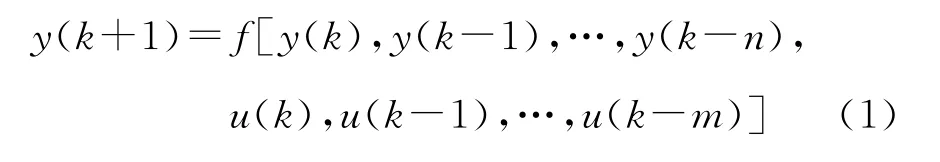
式中：y（k），u（k）分别为系统在k时刻的输出与控制输入；n，m为系统阶数。

由式（1）得到系统的泛模型：

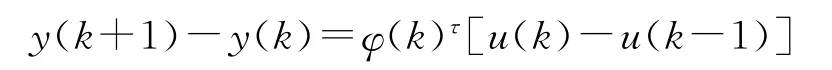
泛模型中的特征向量φ（k）是唯一能够变化而实现自适应的部分，称φ（k）为系统（1）线性化后的伪偏导数。当系统在设定值处于稳定状态时，φ（k）是y（k）关于u（k－1）的梯度。

无模型控制律的一般形式由伪偏导数估计算法和控制律算法两部分组成［6］。

控制律算法：

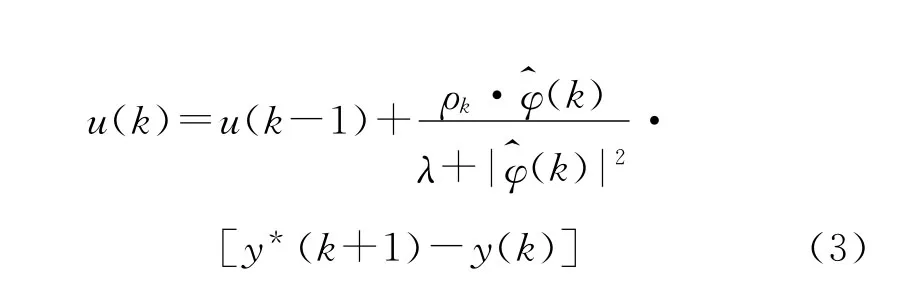
式中：ηk，ρk为学习步长因子；μ，λ 为惩罚因子；（1）为（k）的初值；ε为充分小的正数；y＊（k＋1）为k＋1时刻控制器的给定值。

由控制律可知，无模型自适应控制采用不依赖被控对象的数学模型，仅根据被控对象的I／O数据来得到被控对象的泛模型及控制律，将一般的非线性系统转变为一系列的动态线性时变系统，辨识算法和控制算法在线交替进行，是一种结构自适应算法。

3.2 压下系统MFA控制器设计

通过对无模型自适应算法的分析，得到了式（2）和式（3），该算法将系统当作“黑箱”处理，具有很强的自适应能力。根据以上两式可以设计出应用于冷轧机压下系统的MFA控制器，控制器的算法实现框图如图2所示。

图2给出了MFA控制算法的具体实现方式，框图中虚线部分是计算所需的（k）和Δu（k－1）数据流。根据此框图在Simulink工具箱中设计出MFA控制器，u（k）和（k）的计算利用S函数实现。

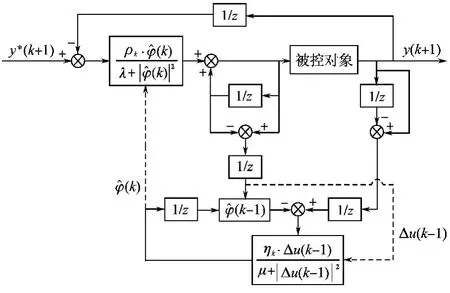
图2 MFA控制器算法实现框图Fig.2 Algorithm of MFA controller block diagram

4 冷轧机压下系统无模型自适应控制仿真

基于Matlab软件平台进行模型仿真，利用Simulink工具箱完成整体模型搭建，由于MFAC算法具有“黑箱”特性，I／O 接口较少，所以将MFA控制器进行封装，封装后的4个接口分别为参考输入、系统输出、反馈输入和控制律输出。系统模型仿真图如图3所示。

图3中压下系统模型作为被控对象，仅用于产生I／O数据，对控制器参数整定无影响。压下系统模型各系数采用现场设备的实际参数计算得出，可以看出，被控对象是一个高阶系统。

图3 压下系统无模型自适应仿真图Fig.3 Screw down system model－free adaptive control simulation

封装后的 MFA 控制器可以对ηk，ρk，μ，λ和S函数的t参数5个参数进行设置，比目前其他无模型控制器的仿真实现更具有灵活性。为了更好地反映生产现场的条件，在整个控制系统中加入0.3s的滞后环节以体现位置测量的滞后性，加入范围为［－0.1，0.1］的白噪声信号以模拟钢坯的高频无规则厚度波动等影响因素对控制系统的干扰。

在综合考虑跟踪能力，控制精度和系统鲁棒性的基础上，设定伪偏导数的学习因子ηk为0.5，惩罚因子μ为1，控制律学习因子ρk为0.7、惩罚因子λ为3，S函数的时间参数t取1，加入幅值为5的阶跃响应作为参考输入，得到图4所示响应曲线。其中包括系统输出的阶跃响应曲线和MFA控制器的控制律曲线。

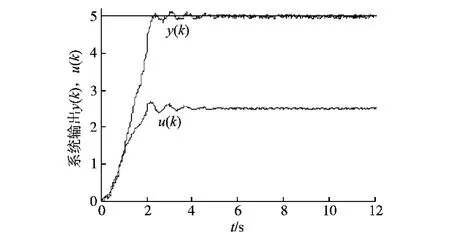
图4 系统阶跃响应及控制律曲线Fig.4 Curves of system step response and control law

从图4中可以看出，在给定参考输入与实际测量值差距较大时，MFA控制器能以较快的速度跟随给定值，经计算，偏差2mm时的跟踪上升时间为36ms；能尽快维持稳定，最大超调量约为4%；对噪声干扰有着较强的抑制，抑制比约为78%。控制律的输出基本与系统输出的曲线一致，反映了控制器与被控对象之间的同步调节。

根据参考文献［7］设计模糊PID控制器作为对比，其中模糊规则49条，为双输入三输出的模糊系统。将2个控制器分别独立作用于压下系统模型，为了突出控制器对高阶非线性系统的控制效果，去掉白噪声干扰，参考输入使用周期为20 s，幅值为1，占空比为50%的脉冲信号，得出如图5所示的响应曲线。

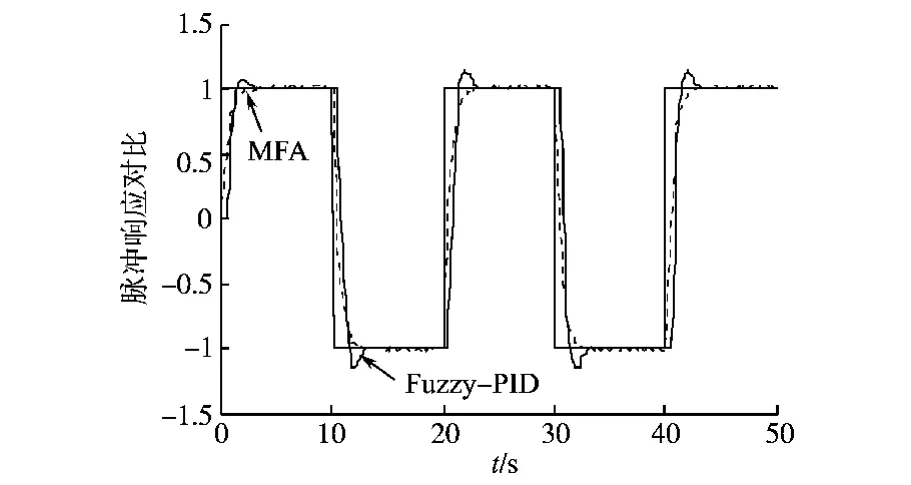
图5 无模型控制器与模糊PID控制器的脉冲响应对比Fig.5 Comparison of step response between MFA controller and fuzzy PID controller

从图5可以看出，模糊PID控制产生较大的超调量，而MFA控制器没有超调，对参考输入的跟随非常精确、稳定。

MFA控制器自身结构的自适应调整特性，使得系统抑制干扰的能力大大提高，更适于过程不确定的被控对象。将上述两种控制器的反馈回路中都加入范围为［－0.05，0.05］的白噪声信号，参考输入是幅值为1的阶跃信号，同时加入0.5s的滞后环节，得出的响应曲线如图6所示。

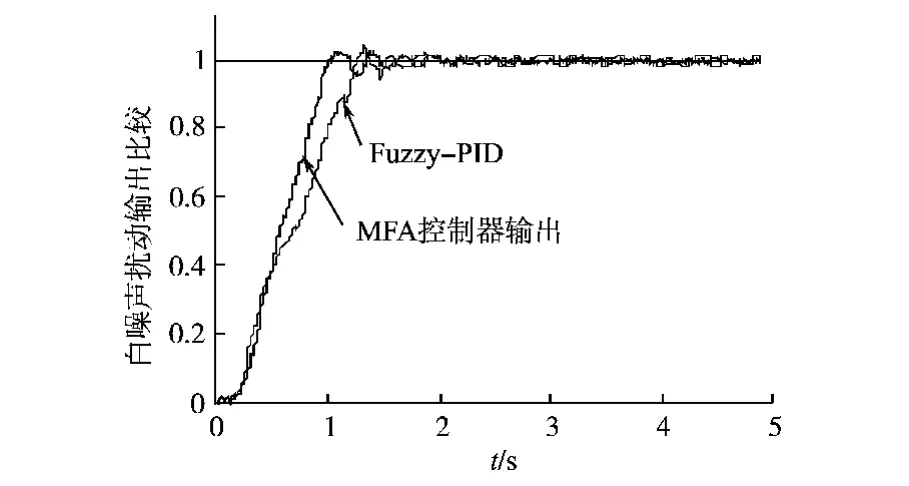
图6 随机扰动下脉冲响应对比Fig.6 Comparison of step response under noise disturbance

由图6可以看出，MFA控制器的输出波动远小于模糊PID控制器的输出，由于白噪声扰动的不规则性使模糊PID控制器频繁调整参数，导致系统响应出现大量尖峰，反映了传统控制器设计过程中参数最优思想的缺点。

5 结论

基于无模型算法的控制器在实验设备上运行，并人为地加入扰动，结果显示控制器能快速克服干扰，辊缝位置调整速度快，精度高，定位精度可达±1μm，与厚度外环控制配合，提高了最终的厚度精度。MFA控制器不基于被控对象的模型，仅需要被控对象的I／O数据，有很强的可移植性，易于实现，可靠性高，控制性能优于模糊PID控制器。在本次设备的改造过程中，只更新控制算法而无须改变轧制工艺就可获得更好的轧制效果，投资小，收益快，有一定的推广价值。

［1］方一鸣，焦晓红，赵现朝，等.自校正PID控制在冷轧带钢厚控系统中的应用［J］.冶金自动化，1999，23（4）：30－33.

［2］蒋爱萍，李秀英，韩志刚.从PID到无模型控制器［J］.控制工程，2005，12（3）：217－220.

［3］陆元章.液压系统的建模与分析［M］.上海：上海交通大学出版社，1989.

［4］赵丽娟，才宏，刘杰.四辊冷连轧机液压压下系统建模研究［J］.机床与液压，2006，34（2）：128－129.

［5］Wang Jing，Ji Chao，Cao Liulin，et al.Design and Realization of Automatic Control System for Boiler Based on Model Free Adaptive Control［C］∥Control and Decision Conference（CCDC），2011：1881－1886.

［6］刘飞祥，李虹.无模型控制律的一种改进算法［J］.工业控制计算机，2008，21（6）：66－67.

［7］王瑶，王晓晔.自适应模糊PID轧机厚度自动控制系统设计［J］.电气传动，2008，38（8）：56－59.