一种基于对角载入的鲁棒MVDR波束形成算法＊

施荣华，孟秋杰，董 健，郭 迎

（中南大学 信息科学与工程学院，湖南 长沙 410083）

自适应波束形成广泛地应用于雷达、系统识别、声纳和移动通信等领域[1－5].MVDR自适应波束形成器在保持信号不变的约束下使噪声输出功率最小，具有良好的弱信号检测和高分辨力性能，因此得到广泛的应用.但是由于外部环境、信源、传感器阵列等诸多条件的复杂变化，导致信号方向向量出现偏差，使传统的MVDR波束形成算法的性能下降.为了克服各种误差引起的性能下降，一些学者近几十年进行了大量研究来提高自适应波束形成的稳健性，其中最具代表性的方法有3种：特征空间（ESB）法、线性约束（LCMV）法和对角加载（LSMI）法.特征空间法[6]具有较快的收敛速度，但它需要准确估计信号子空间维数，当子空间维数过估计或欠估计时算法失效；线性约束法[7]通过适当的约束条件使得自适应波束满足一定的稳健条件，但只适用于观察方向失配的情况；对角加载法：文献[8]对协方差矩阵沿其对角线加一正常数后再用采样协方差矩阵求逆方法求得自适应权值提高自适应波束形成器的稳健性.由于加载量被固定，不随期望信号的信噪比和导向矢量的误差变化而变化，当信噪比增加时，输出信干噪比会明显恶化.文献[9]采用最差性能最优化思想，提高了波束形成器的鲁棒性，但是该算法计算复杂度高，不便于工程实现；文献[10]采用矩阵锥消方式，通过对协方差矩阵点乘一个给定误差范围，提高波束形成器的稳健性，但是由于给定的误差范围不好控制，效果并不理想.

本文考虑到方向向量最大允许偏差的情况，提出了一种新的基于对角载入的MVDR自适应波束形成算法.由于该算法是在最差性能下的优化问题，因此在一定范围内，对角加载量的大小对该算法的性能影响不大；同时在求解过程中进行降维处理，避免矩阵求逆，大大地降低运算量，便于工程实现.仿真实验验证了所提鲁棒算法的有效性和可行性.

1 传统算法描述

1.1 信号模型

考虑M元各向同性的均匀线阵，阵元间距为d，期望信号波达方向为θ0，有D－1个干扰源，波达方向分别为 ｛θ1，θ2，...，θD－1｝，其中，M ＞D .以阵列的第1个阵元为基准，各个窄带信号在基准阵元的复包络分别为s0（t），s1（t），...，sD－1（t），则第l个阵元端接收的信号为：

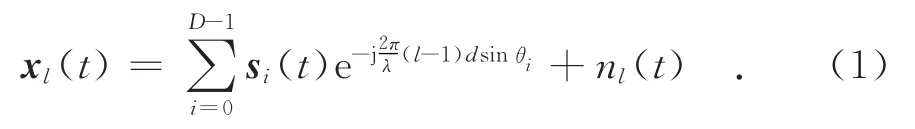
式中：λ为信号的波长；nl（t）为第l个阵元上均值为零、方差为σ2n的白噪声.天线阵列的接收向量[11]为：

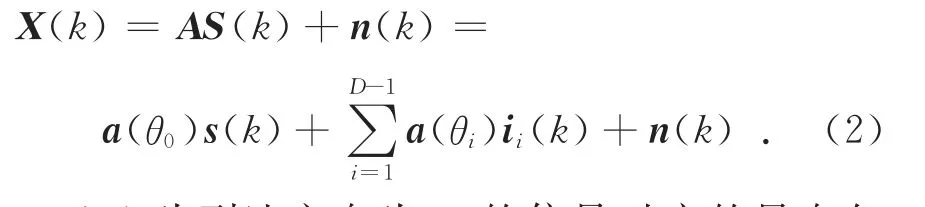
式中：a（θi）为到达方向为θi的信号对应的导向矢量.阵列输出为：

阵列输出的信干噪比为：

式中：Rs为阵列期望信号的协方差矩阵，Ri＋n为干扰和噪声的协方差矩阵.

在信号处理中，为保证期望信号正常接收，应尽量减弱和抑制干扰信号，即增大系统的输出信干噪比.在自适应阵列天线系统中，通过调整权重向量，可使系统的输出信干噪比达到最优值，即：

式中：σ2s为信号的功率.式（5）给出了式（4）的输出信干噪比SINR的上限.

1.2 MVDR波束形成算法

MVDR波束形成器是使噪声以及来自非θ方向的任何干扰的功率为最小，但又能保持在观测方向θ上的信号功率不变，其代价函数为：

式中：a（θ）为期望信号的方向向量.令

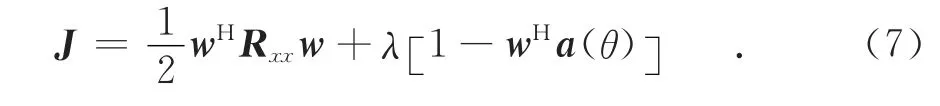
求式（7）的梯度并令其为零，得到：

解得权重向量为：

把式（9）代入式（6）的约束条件中，求得：

把式（10）代入式（9）中求出最优权重向量

MVDR算法要求准确知道信号的方向向量，而在实际应用环境中，由于信号的方向向量存在偏差，这使得自适应算法的性能下降，输出的信干噪比偏离最优值.MVDR波束形成器，不能有效地抑制干扰，产生严重的信号相消现象.

2 鲁棒MVDR波束形成算法

针对信号的方向向量误差导致传统MVDR算法的性能下降，本文提出了基于对角载入的鲁棒MVDR波束形成算法.该算法考虑信号方向向量的偏差对MVDR算法性能的影响，通过对协方差矩阵进行修正，得到最优的权重向量，有效地抑制了偏差对输出性能的影响，具有很强的鲁棒性.

假设信号方向向量的偏差为Δ，ε为最大偏移量：

那么信号的实际方向向量属于集合：

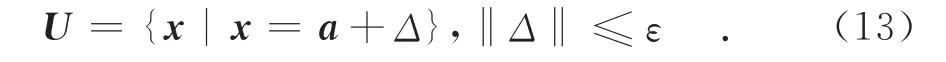
在观测信号方向上无失真响应的绝对值不小于1.

把式（14）的不等式约束转化为等式约束[11]的形式可得：

则式（6）可写为

进一步得到代价函数为：

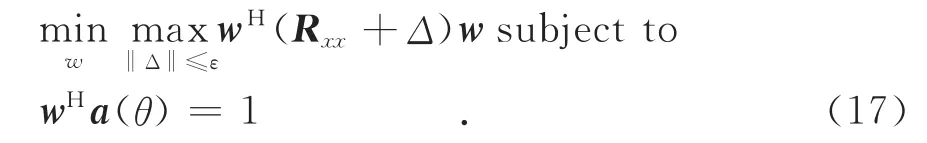
对代价函数式（17）的求解，本文将其转化为两个最优化问题.首先求其子函数的最大值：

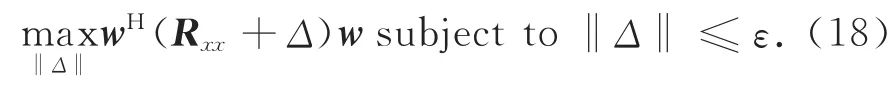
利用拉格朗日方法求得：

将式（19）代入式（18）中得到：

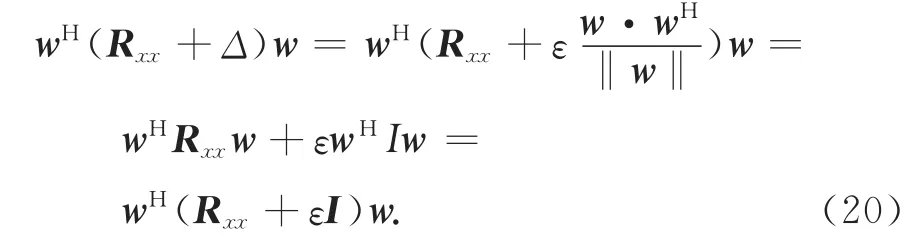
然后求代价函数的最小值，代价函数式（17）可以重写为

其中：a（θ）为期望信号的方向向量.令

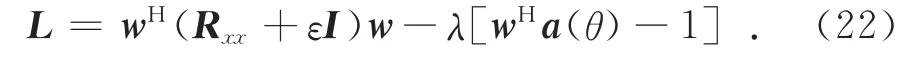
其中：λ为拉格朗日因子，对式（22）求梯度

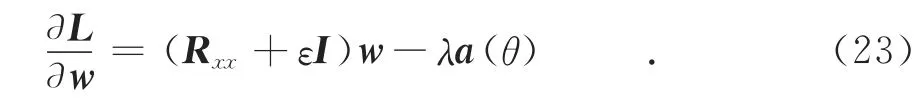
令其梯度等于零等到最优权向量

权重向量是通过对矩阵直接求逆得到的最优值，其计算量会随着阵元数目和采样数目的增加而剧增.本文采用递推算法，避免矩阵直接求逆，将计算复杂度从多维降到一维.利用式（17）得到基于对角载入的鲁棒MVDR算法的递推公式为

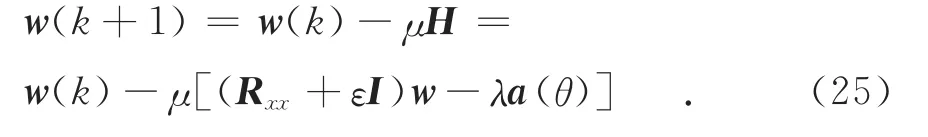
其中：μ为步长因子，将式（25）代入式（21）的约束条件，得到：

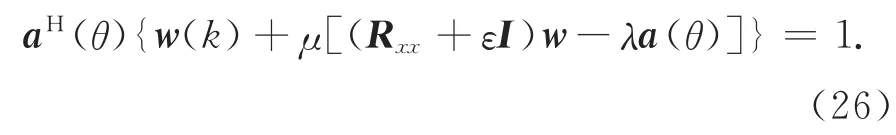
通过求解式（26）得到拉格朗日因子λ为：

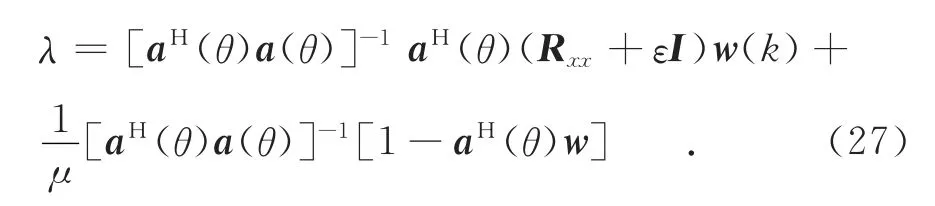
代入求得最优权向量公式为：

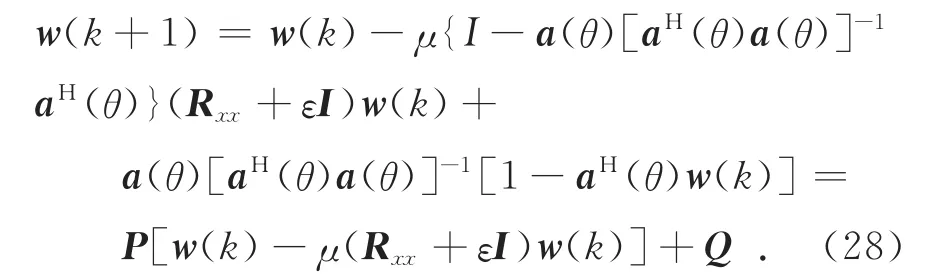
其中：

从式（28）中可见，最优权向量的计算复杂度为一维，便于工程实现.

3 仿真实验结果

实验考虑10个阵元的等距线阵，阵元间距为半个波长，采样次数为4 096，对于每一点都分别进行100次的仿真实验.假设期望信号的波达方向为0°，两个干扰源的波达方向分别为30°和50°.

实验一 阵列方向图的比较

设仿真条件为：SNR＝10dB，对角载入因子为ε＝2，信号的实际波达方向为2°，即偏差为2°.图1给出了方向向量无偏差情况下两种算法在信号波达方向上形成的阵列方向图.图中垂直的点划线表明了信号的实际波达方向.从图1中可以看出，本文算法在期望信号处形成了很高的增益，达到了提取有用信号的目的.图2给出了方向向量存在偏差时的阵列方向图，为了便于观察，仿真时将本文算法的输出曲线垂直下移.从图2中可以看出，传统MVDR算法在有用信号处形成零陷，而本文所提的算法在存在偏差的情况下也有很强的增益，避免了信号相消现象，对信号方向向量偏差的敏感度较低，具有很好的鲁棒性.

在工程实现中，方向向量最大允许偏差的值一般不会超过2°，本文选取2°偏差进行仿真实验，仿真结果说明该算法具有很好的输出性能，因此该算法具有一定的适用性.

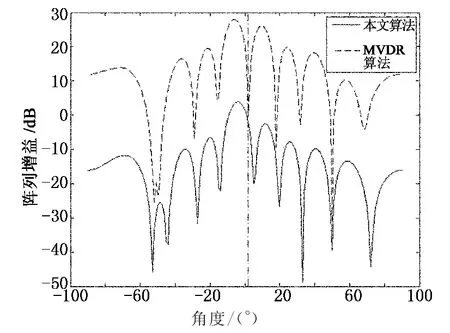
图1 两种算法阵列方向图（无偏差）Fig.1 Array pattern of the two algorithms（no deviation）

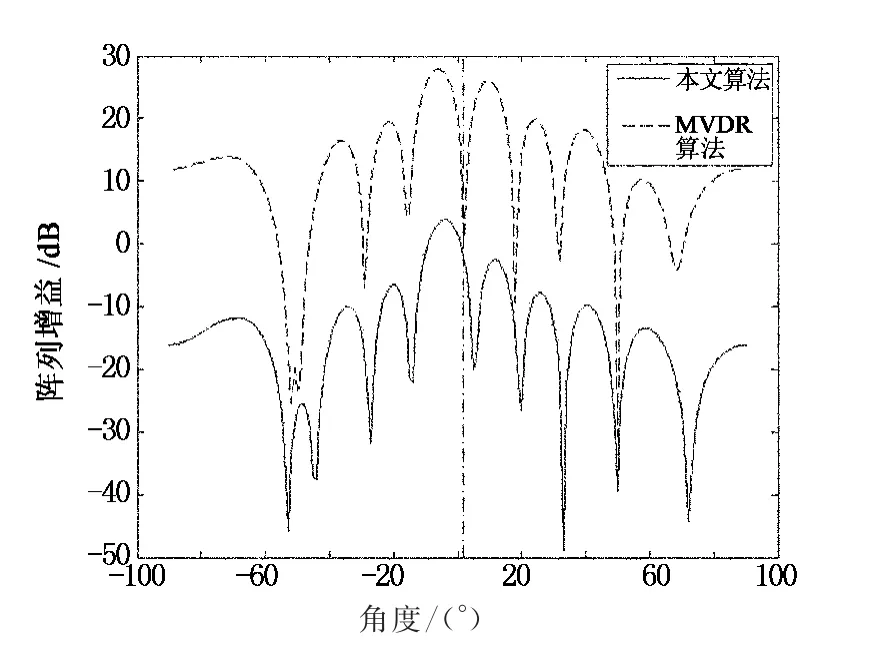
图2 两种算法阵列方向图（2°偏差）Fig.2 Array pattern of the two algorithms（2°deviation）

实验二 输出信干噪比SINR的比较

设仿真条件为：信噪比SNR＝10dB，信号的实际波达方向为2°，即偏差为2°.图3给出了无偏差情况下阵列输出的信干噪比SINR随采样数目的变化曲线.图4给出了存在2°偏差的情况下阵列输出的信干噪比SINR随采样数目的变化曲线.

从本实验中可以看出，与传统的MVDR算法相比，本文所提的算法对信号方向向量的偏差具有很强的鲁棒性，输出的信干噪比SINR要明显优于传统的MVDR算法.

图3 阵列输出的信干噪比（无偏差）Fig.3 Output SINR of the two algorithms（no deviation）

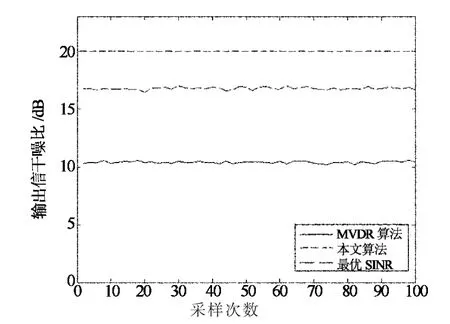
图4 阵列输出的信干噪比（2°偏差）Fig.4 Output SINR of the two algorithms（2°deviation）

实验三 不同对角载入因子的比较

设仿真条件为：信噪比SNR＝10dB，信号的实际波达方向为2°，即偏差为2°.图5给出了ε＝2和ε＝4两种不同对角载入因子情况下所提算法的阵列方向图，图6给出了对角载入因子分别为ε＝2和ε＝1.5情况下所提算法的阵列方向图.

综合图5和图6可以看出，本文算法在选取不同对角载入因子ε＝1.5，ε＝2，ε＝4时，对于方向向量偏差均具有较强的鲁棒性；这说明，在一定范围内对角载入因子的不同取值对本文算法的性能影响不大.

图5 对角载入因子ε＝2和ε＝4Fig.5 Array pattern of the diagonal factor between 2and 4

图6 对角载入因子ε＝2和ε＝1.5Fig.6 Array pattern of the diagonal factor between 2and 1.5

4 结 论

针对方向向量存在偏差时所导致传统MVDR波束形成器性能急剧下降的问题，本文提出了一种基于对角载入的鲁棒MVDR波束形成算法.该算法对协方差矩阵的估计误差进行约束，提高了算法的稳健性；在求解过程中进行降维处理，降低了计算量，易于实时实现.该算法有效地抑制了方向向量偏差对MVDR波束形成器输出性能的影响，具有较强的鲁棒性.仿真实验表明：与传统MVDR算法相比，所提算法具有更好的输出性能，在一定范围内对角载入因子的取值对所提算法的性能影响不大.

[1] KROLIK J L.The performance of matched－field beamformers with Mediterranean vertical array data[J].IEEE Trans Signal Processing，1996，44（10）：2605－2611.

[2] 曾凡仔，陈苗苗，罗娟，等.一种能量有效的无线传感网络节点跟踪算法[J].湖南大学学报：自然科学版，2009，36（1）：81－84.ZENG Fan－zai，CHEN Miao－miao，LUO Juan，etal.An energy efficient nodes tracking algorithm in wireless sensor network[J].Journal of Hunan University：Natural Sciences.2009，36（1）：81－84.（In Chinese）

[3] 冯琳，段复建 .基于锥模型的非单调自适应信赖域算法[J].山西大学学报：自然科学版，2011，34（4）：580－586.FENG Lin，DUAN Fu－jian.A Non－monotone self－adaptive trust region method based on the conic model[J].Journal of Shanxi University：Natural Science Edition，2011，43（4）：580－586.（In Chinese）

[4] 何松华，程凡永，陈威兵，等.基于数据外推的限带信号最大似然谱估计[J].湖南大学学报：自然科学版，2009，36（3）：85－88.HE Song－hua，CHENG Fan－yong，CHEN Wei－bing，etal.Band－limited signal spectrum estimation based on data extropolation and maximum likelihood criterion[J].Journal of Hunan University：Natural Sciences，2009，36（3）：85－88.（In Chinese）

[5] GERSHMAN A B，TURCHIN V I，ZVEREV V A.Experimental results of localization of moving underwater signal by adaptive beamforming [J].IEEE Trans Signal Processing，1995，43（10）：2249－2257.

[6] 周讳，唐南，于美华.一种快速的特征空间自适应波束形成算法[J].电子信息对抗技术，2009，24（4）：39－42.ZHOU Hu，TANG Nan，YU Mei－hua.A fast eigenspacebased adaptive beamforming algorithm[J].Electronic Information Against Technology，2009，24（4）：39－ 42.（In Chinese）

[7] HARRY LAND VAN TREES.最优阵列处理技术[M].汤俊译 .北京：清华大学出版社，2008：382－392.HARRY LAND VAN TREES，TRANS.TANG Jun.Optimum array processing part IV of detection，estimation，and modulation theory[M].TANG Jun Translate.Beijing：Tsinghua University Press，2008：382－392.（In Chinese）

[8] CARLSON B D.Covariance matrix estimation errors and diagonal loading in adaptive arrays[J].IEEE Trans on Aerospace and Electronic Systems，1988，24（4）：397－401.

[9] VOROBYOV S A，GERSHMAN A B，LUO Z Q.Robust adaptive beamforming using worst－case performance optimization：a solution to the signal mismatch problem [J].IEEE Trans Signal Processing（S1053－587X），2003，51（2）：313－323.

[10] GUERCI J R.Theory and application of covariance matrix taper for robust adaptive beamforming[J].IEEE Trans on Signal Processing，1999，47（4）：977－985.

[11] 张贤达，保铮.通信信号处理[M].北京：国防工业出版社，2000：324－326.ZHANG Xian－da，BAO Zheng.Communication signal processing[M].Beijing：China National Defence Industry Press，2000：324－326.（In Chinese）