一种基于DNA自组装模型求解最大团问题的算法＊

周炎涛，李肯立，罗 兴，黎福海，朱 青

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082； 2.湖南大学 信息科学与工程学院，湖南 长沙 410082）

最大团问题（Maximum clique problem，MCP）又称为最大独立集问题，是图论中的一个经典组合优化问题，也是一类NP完全问题[1].求解MCP算法主要有二类：确定性算法和启发式算法，前者有回溯法、分支限界法等 .随着问题规模的增大（顶点增多和边密度变大），求解问题的时间复杂度越来越高，确定性算法显得无能为力，不能有效地解决这些NP完全问题 .后者有蚁群算法、顺序贪婪算法、DLS－MC算法和智能搜索算法等，大部分确定性算法所不能解决的图，用启发式算法都能得到有效解决，但启发式算法不一定能找到最优解，有时只能找到近似值[2].近年来，常借鉴算法之间优势互补策略，形成新的混合启发式算法来求解最大团问题[3].

DNA计算是应用分子生物技术进行计算的新方法，具有高度并行性、大容量、低能耗等特点，为解决NP完全问题开辟了一条新途径[4].自Adleman首次运用DNA计算来解决NP问题以来[5]，研究者对最大团问题的分子求解方法进行了很多有益的尝试，如基于粘贴模型的最大团问题算法[6]、质粒DNA算法[7]、闭环求解最大团问题算法[8]等，但这些方法均存在实验操作步骤过多、活体内不易操作以及环化效率不高等弊端.此外，Brun采用自组装DNA计算给出了路径寻找问题[9]，以及可满足性问题的自组装计算模型的解决方案[10].文献[11]在分布式系统中建立自组装模型解决自由等待一致性问题 .文献[12]将AuNP自组装聚合色变与DNA计算相结合，构建了系列基本逻辑计算模型，等等.

在DNA计算机研究中，所建模型的好坏直接影响着DNA计算中诸多问题，如编码的难易程度、整个生物操作或生化反应的设计、解空间的大小、计算时间多少、应用范围以及通用性的程度等.目前DNA计算模型有很多[13]，其中自组装DNA计算模型是通过DNA分子间的相互作用形成特定的构型来完成计算过程 .它组合了DNA计算、Ting理论和DNA纳米技术，成为目前备受关注的模型之一[14－15].在计算过程中，它避免了其他DNA计算模型所需要的众多实验操作次数，减少了操作带来的时间消耗和误差倾向.分子自组装体系是一个高度组织、高度有序、结构化、功能化和信息化的复杂系统，对研究分子自组装特性并求解最大团问题极有价值.本文采用DNA自组装模型，设计出相应的DNA tiles分子，利用基因工程的生物操作，提出一种基于DNA自组装模型求解最大团问题的算法.该算法实验操作复杂度为常数级，既大大减少了因为人为实验操作所带来的误差，又保证了实验结果的准确性.

1 DNA自组装模型

DNA的自组装可形成一维、二维、三维结构.本文主要利用其形成的二维平面结构来解决最大团问题.1998年，根据 Wang的tiles理论，Winfree设计了双交叉分子DX[16]，这个DX就充当了tiles的作用，通过自组装就能实现所需的计算.理论上有5种可能的DX结构，但通过大量实验证明，只有DAO和DAE这2种结构是稳定的[16].抽象的DAO和DAE结构如图1所示.

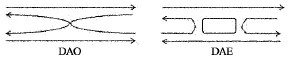
图1 DAO，DAE抽象结构Fig.1 Abstractive structures of DAO and DAE

观察图1可知，DAO结构包含4条DNA链，其中有2条链分布在2条双螺旋上，另外2条分布在一条双螺旋上 .相比之下，DAE结构包含5条DNA链，其中有3条链分布在2条双螺旋上，另外2条链分布在一条双螺旋上.由于DX可有4个粘性末端，故可利用这些粘性末端来实现所需要的计算.Winfree使用了带颜色的tiles来模拟双交叉分子的计算过程，规定只有具有相同颜色的边才能够结合形成较大的格局，其反应过程如图2所示.

图2 DX计算过程模拟Fig.2 Process simulation of DX computing

根据Wang的tiles理论模型的形式化描述以及Yuriy Brun引入DNA 的tiles自组装模型[17]，结合最大团问题的特点可将基于DAE结构的自组装模型表示为S＝〈T，g，τ〉，其中T为DAE块的集合，g为能量函数，τ为常数.相应的符号描述如下：

1）Σ：DAE块中所有粘性末端所表示符号的集合（即所要参与计算的符号的集合）；

2）D′＝ ｛UL，DL，UR，DR｝：分别表示DAE块的左上角、左下角、右上角和右下角4个位置；

3）｛σUL，σDL，σUR，σDR｝∈Σ4：DAE块的形式化描述，代表DAE块4个位置分别所表示的符号；

4）（x，y）∈Z2：表示位置；

5）D＝｛N，E，S，W｝：表示4个方向函数，且满足：

●∀（x，y）∈Z2，N（x，y）＝（x，y＋1），E（x，y）＝（x＋1，y），S（x，y）＝（x，y－1），W （x，y）＝（x－1，y）；

●若位置（x，y）与（x’，y’）相邻，则∃d∈D，使得d（x，y）＝ （x’，y’）.

6）bdd（t）∈Σ，其中t∈T，d∈D’：表示t的位置d所表示的符号；

7）函数g：Σ×Σ→R，此函数定义如下：

●∀σ∈Σ，则g（null，σ）＝0；

●若g（σ，σ’）＝0（其中σ，σ’∈Σ），则σ≠σ’；

●∀σ≠null，有g（σ，σ）＝1；

●∀σ≠σ’，有g（σ，σ’）＝0.

8）函数A：Z×Z→T，此函数有如下特点：

●若A（x，y）≠empty，则（x，y）∈A；

●若只有有限个不同的（x，y）∈A，则A为一个有限集.

9）A是一个格局，若一个DAE块t能在位置（x，y）产生一个新的格局A’，需要满足以下条件：

●（x，y）∉A；

●Σd∈D’，d’∈Dg（bdd（t），bdd－1（A（d’（x，y））））≥τ，其中d与d－1为相对的方向，如：UR与DL相对.

●∀（u，v）∈Z2，（u，v）≠ （x，y），则A’（u，v）＝A（u，v）；

●A（x，y）＝t.

2 算法设计步骤

2.1 算法设计思路

基于DNA自组装模型的算法设计利用的是“堆积木”的思想，其具体算法设计思路如下：

1）设计初始分子，使之组装成所有可能结果；

2）分析问题，找出问题正确结果所需满足的条件；

3）根据2）条件限制，设计规则分子，判定1）中结果正确性；

4）搜索正确结果，得到所需答案.

本文按照上述步骤设计相应的DAE块，然后通过基因工程的相应生物操作，利用凝胶电泳和荧光标记技术提取得到最终结果.相应生物操作描述[18]如下：

1）合并（merge）：给定试管P1和P2，操作∪（P1，P2）＝P1∪P2表示将试管P1和P2合并到一个试管中而不改变P1和P2中的任何链.

2）提取（extract）：给定试管P1和P2，操作P2＝extract（P1）表示提取试管P1中具有某种特征的DNA分子到试管P2.

3）退火（anneal）：给定试管P，操作Anneal（P）将试管P中的所有DNA单链变成双链.

4）荧光标记（fluorescence labeling）：给定试管P，该操作将具有某种特征的DNA分子作标记.

5）凝胶电泳（gel electrophoresis）：给定试管P，该操作将试管中DNA分子按照分子大小进行分离.

2.2 设计初始分子

设G＝｛V，E｝，其中V＝｛v1，v2，… ，vn｝，则任何顶点子集都可能是图G的团，则初始分子设计如图3所示.其中，s和e是控制自组装反应的始端和终端，与图G无关；i，j∈｛1，2，…，n｝，且i＜j.分析可知：所有初始分子的种类为2n2－7n＋8.

若顶点子集为｛1，2｝，则退火反应之后则形成如图4所示结构.若顶点子集为｛1，2，3｝，则退火后反应之后形成如图5所示结构.

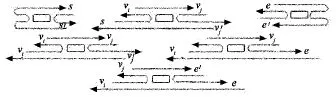
图3 初始分子Fig.3 Initial moleculars

图4 顶点子集｛1，2｝形成的结构Fig.4 Forming structure of vertex subset｛1，2｝

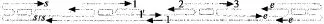
图5 顶点子集｛1，2，3｝形成的结构Fig.5 Forming structure of vertex subset｛1，2，3｝

引理1 若Σ1＝｛s，e，v1，v2，…，vn｝，T1为按上述方式设计的初始分子DAE块的集合，τ＝1，则形成的自组装系统S1＝〈T1，g，τ〉.不失一般性，比如顶点子集为｛v1，v2，… ，vk｝，经过退火反应后则会形成如下格局A1：

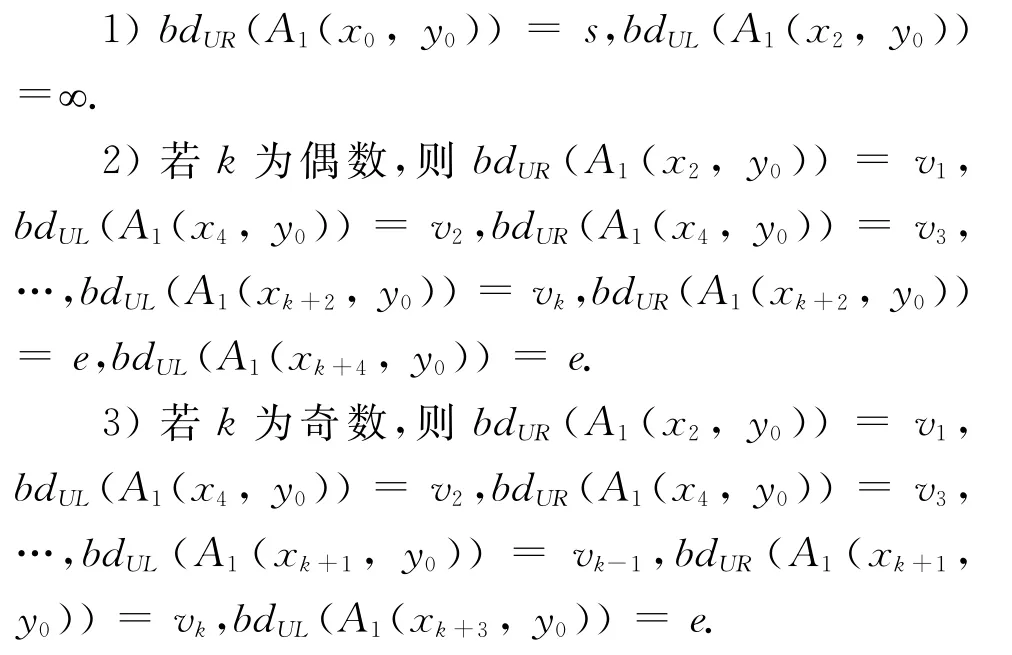
证 根据T1中的DAE块的特点可知，起始端为｛null，null，s，s｝，所以bdUR（A1（x0，y0））＝s.已知τ＝1，所以只需要一边能够结合就能够产生新的格局.又已知顶点子集为｛v1，v2，… ，vk｝，所以∃DAE块｛∞，s，v1，v1｝，所以｛null，null，s，s｝与｛∞，s，v1，v1｝能够结合产生新的格局.则此时bdUL（A1（x2，y0））＝∞，bdUR（A1（x2，y0））＝v1.

同理可知：当k为偶数时，bdUL（A1（x4，y0））＝v2，bdUR（A1（x4，y0））＝v3，…，bdUL（A1（xk＋2，y0））＝vk，bdUR（A1（xk＋2，y0））＝e，bdUL（A1（xk＋4，y0））＝e.

当k为奇数时，bdUL（A1（x4，y0））＝v2，bdUR（A1（x4，y0））＝v3，…，bdUL（A1（xk＋1，y0））＝vk－1，bdUR（A1（xk＋1，y0））＝vk，bdUL（A1（xk＋3，y0））＝e.

（2）要根据运行方式来调整好继电保护装置的保护功能、保护范围以及相关的定制等等，对电网中所有有关的信息进行综合，再实时修正好保护定值。

证毕.

2.3 设计规则分子

我们把规则分子的DAE块设计成如图6所示.

图6 两顶点邻接时DAE块Fig.6 DAE block with adjoining vertexes

若输入顶点a，b在图中是邻接的，则存在上述DAE块，使其输出时交换顶点变成b，a.考虑到边界条件，则可以把规则分子设计成如图7.

图7 规则分子Fig.7 Regular moleculars

其中s为始端，e为终端，与图G无关.节点a，b邻接，且a，b，c，d∈｛v1，v2，…，vn－1，vn，∞｝，所需DAE块种类为｜E｜＋2n＋1.

引理2 在格局A1的基础上，若T2为按上述方式设计的规则分子的集合，并且τ＝2，则形成的自组装系统S2＝〈T2，g，τ〉.若G对于生成的格局A1中的所有顶点都相邻，则系统S2会生成格局A2，其中bdUR（A2（xk＋1，yk＋1））＝∞，bdUL（A2（xk＋3，yk＋1））＝e.若G对于生成的格局A1中存在两个顶点不相邻，则系统S2不会生成上述格局A2.

证k为偶数且图G对于生成的格局A1中的所有的顶点都相邻，则形成的A1如引理1中所述.由于τ＝2，所以需要两边能够结合才能产生新的格局.又因为所有的顶点都相邻，所以对于任意两个顶点vi，vj都存在 DAE 块｛vj，vi，vi，vj｝，即每经过一轮比较∞都会向后移动，所以∞终会移动到末尾，即bdUR（A2（xk＋1，yk＋1））＝ ∞，且bdUL（A2（xk＋3，yk＋1））＝e.同理可知：若k为奇数时，bdUR（A2（xk＋1，yk＋1））＝∞，bdUL（A2（xk＋2，yk＋1））＝e.故系统S2会生成格局A2.

反之，若A1中存在两个顶点不相邻.不失一般性，假设存在两个顶点vi，vj不相邻，则不会存在DAE块｛vj，vi，vi，vj｝.由于τ＝2，当反应进行到此后，格局就不会再增高，∞也就不会移动到末尾.故不能形成格局A2.

证毕.

2.4 设计检测分子

图8 检测分子Fig.8 Detected moleculars

i，j∈｛1，2，…，n－1，n｝，并且利用荧光标记技术在上图中最左边的DNA分子加上与其他DAE块不同颜色的荧光.则这些DAE块种类共计n2＋1种.

若加入规则分子后能够形成格局A2，则加入检测分子后就能够形成一个完整的格局，否则就不能形成一个完整稳定的格局（即该格局没有粘性末端可提供给其他DAE块结合，并且该格局中拥有带有荧光标记的检测分子）.

综上所述，设计初始分子所需的DAE块种类为2n2－7n＋8；设计规则分子所需的DAE块种类为｜E｜＋2n＋1；设计检测分子所需的DAE块的种类为n2＋1.总共需要的DAE块种类为3n2－5n＋｜E｜＋10.所以需要的DAE块的种类为Θ（n2＋｜E｜），说明设计这些DAE块是可行的.

3 基于DNA自组装模型求解最大团问题

3.1 算法步骤

算法基于自组装模型的最大团问题DNA算法.

输入：图G＝｛V，E｝，以及根据图G并按上述方式设计的tiles集T1，T2，T3.

输出：图G的最大团.

7）T’end＝ Extract（T），提取在6）中所观测到的分子块，将其放入试管T′end；

8）使用凝胶电泳技术将T中的分子块按照大小进行分离，通过激光共焦距显微镜观察分子块最大的DNA块；

9）Tend＝Extract（T′end），提取8）中所观察的最大的DNA块，将其放入试管Tend.

引理3 有a1，a2，a3，…，an个顶点，按照以下方式进行n轮比较，则这n个顶点每两个顶点都会比较一次，即总共比较Cn2＝n（n－1）／2次.

证 当n为偶数时，奇数轮比较（n／2）－1次，偶数轮比较n／2次，则总共比较的次数为（n／2）（n／2－1）＋ （n／2）（n／2）＝n（n－1）／2＝Cn2.

同理可知：当n为奇数时，总共比较次数为n（n－1）／2＝Cn2.

证毕.

定理1 若算法中Tend不为空，则Tend中所代表的团即为所求图的最大团；否则该图的任意两个顶点都不邻接.

证 若Tend不为空，则Tend中的顶点集是按照引理1中的方式进行比较.由引理1可知：Tend中的顶点集共进行了Cn2次比较.又由于两个顶点比较之后一个顶点向左移动，另外一个顶点向右移动，则这两个顶点不会重复比较，所以每两个顶点都比较过一次.说明这n个顶点两两邻接，即此顶点子集的导出子图就为此图的一个团.又由算法1的8）可知Tend中所表示顶点集都规模最大，所以Tend中所代表的团即为所求图的最大团.反之，若Tend为空，则说明图G的任意顶点子集的导出子图都不是团，即该图的任意两个顶点都不邻接.

证毕.

3.2 算法复杂性

文中2.2设计初始分子所需的DAE块种类为2n2－7n＋8；2.3设计规则分子所需的DAE块种类为｜E｜＋2n＋1；2.4设计检测分子所需的DAE块的种类为n2＋1.则总共需要的DAE块种类为3n2－5n＋｜E｜＋10.所以需要的DAE块的种类为Θ（n2＋｜E｜），即算法设计tiles的种类为Θ（n2＋｜E｜）.算法1（基于自组装模型的最大团问题DNA算法）生物操作为9步，即其生物操作复杂性为Θ（1）.

3.3 示 例

给定图G＝｛V，E｝，其中V＝｛1，2，3，4，5｝，E＝｛（1，2），（2，3），（3，4），（4，5），（2，5），（2，4），（3，5）｝，如图9所示.

图9 5个顶点无向图Fig.9 Graph of 5vertexes

结合3.1的算法步骤，则求得最大团的步骤为如图10所示 .在试管T1中加入连接酶，并使用退火操作，使其初始分子充分反应，则会形成不同的顶点子集，如图10（a）形成的顶点子集为｛2，3，4，5｝.

将试管T1，T2中的DAE块合并到试管T，之后在试管T中加入连接酶，并使用退火操作.此步骤实际上是加入规则分子，用以判断前面的顶点子集是否为团.如图10（b）即为加入规则分子去判断顶点子集｛2，3，4，5｝是否为团.

最后加入检测分子，便于检测顶点子集的导出子图是否为团.经过上述步骤后，凡是能够形成如图10（c）所示的结构，则说明该导出子图即为团，即该图中存在有荧光标记的DNA分子.

图10 图G最大团计算Fig.10 Computing maximum clique of G

4 结 论

自组装技术能最底层揭示DNA计算的本质，它是一种由简单到复杂、从无序到有序、由多组分收敛到单一组分不断自我修正、自我完善的过程.本文采用DNA自组装模型，设计出相应的DNA tiles分子，利用基因工程的生物操作，提出一种基于DNA自组装模型求解最大团问题的算法 .该算法实验操作复杂度为常数级，既大大减少了因为人为实验操作所带来的误差，又保证了实验结果的准确性，对DNA计算和DNA计算机的研究来说，是一次有意义的实践.目前DNA计算模型的DNA编码已经从一维结构发展到了三维结构 .相对于其他的计算模型，从理论上已表明，使用三维DNA图结构可以明显减少解决最大团问题所需的时间和步骤，而且由于它能直观地反映图结构，用它建立计算模型可能会使一些传统的难解问题得以解决.

本文主要利用其形成的二维平面结构来解决最大团问题 .在技术层面上，将这种二维DNA分子组装成三维DNA图结构模型还存在很多需要解决的问题.目前对复杂三维DNA结构进行普通的实验操作还少有研究，且与它相关联的酶处理操作也容易发生错误.随着DNA计算研究的深入，三维DNA计算也将会有更好的发展 .此外，将分子计算与量子计算紧密地结合在一起，为未来的新型计算技术提供了发展的可能.伴随分子操控技术的发展，相信DNA计算在信息处理、密码技术、纳米智能机器和纳电子学等多个领域将会有更多的潜在应用.

[1] OUYANG Q，KAPLAN P D ，LIU S，et al.DNA solution of the maximal clique problem[J].Science，1997，278：446－449.

[2] PULLAN W，HOOS H H.Dynamic local search for the maximum clique problem[J].Journa l of Artificial Intelligence Research，2006，25：159－185.

[3] KATAYAMA K，KOHMURA A，KOHMOTO K，et al.Memetic algorithm with strategic controller for the maximum clique problem[C]∥Taiwan：TaiChung：Proceedings of the 2011ACM Symposium on Applied Computing，2011：1062－1069.

[4] SHARRMA J，CHHABRA R，CHENG A，et al.Control of self－assembly of DNA tubules through integration of gold nanoparticles[J].Science，2009，323：112－116.

[5] ADLEMAN L M.Molecular computation of solutions to combinatorial problems[J].Science，1994，266（11）：1021－1024.

[6] 周康，刘朔，覃磊，等.基于粘贴模型的最大团问题算法[J].华中科技大学学报：自然科学版，2010，38（9）：89－92.ZHOU Kang，LIU Shuo，QIN Lei，et al.Sticker model－based DNA algorithm of maximum clique problem[J].Huazhong Univ of Sci ＆Tech：Natural Science Edition，2010，38（9）：89－92.（In Chinese）

[7] HEAD T，ROZENBERG G，BLADERGROEN R B，et al.Computing with DNA by operating on plasmids[J].Bio Systems，2000，57：87－93.

[8] 张成，杨静，许进，等.DNA缩短法计算模型求解最大独立集问题[J].科学通报，2009，54（24）：3913－3919.ZHANG Cheng，YANG Jing，XU Jin，et al.A DNA length reducing computing model for maximum independent set problem[J].Chinese Sci Bull，2009，54（24）：3913－3919.（In Chinese）

[9] BRUN Y，REISHUS D.Path finding in the tile assembly model[J].Theoretical Computer Science，2009，410（15）：1461－1472.

[10] BRUN Y.Solving satisfiability in the tile assembly model with a constant－size tileset[J].Journal of Algorithma，2008，63（4）：151－166.

[11] STERLING A.Distributed agreement in tile self－assembly[J].Natural Computing：an International Journal，2011，10（1）：337－355.

[12] 张成，杨静，许进.自组装DNA／纳米颗粒分子逻辑计算模型[J].科学通报，2011，56（27）：2276－2282.ZHANG Cheng，YANG Jing，XU Jin.Molecular logic computing model based on self－assembly of DNA nanoparticles[J].Chinese Sci Bull，2011，56（27）：2276－2282.（In Chinese）

[13] XU Jin，TAN Gang－jun，FAN Yue－ke，et al.DNA computer principle，advances and difficulties（Ⅳ）：on the models of DNA computer[J].Chinese Journal of Computers，2007，30（6）：881－893.

[14] 张勋才.自组装DNA计算模型的研究及应用[D].武汉：华中科技大学计算机工程与技术学院，2009.5.ZHANG Xun－cai.The reserch and applications of DNA computing by self－assembly[D].Wuhan：Huazhong Univ of Sci＆Tech，2009.5.（In Chinese）

[15] HE Yu，MAO Cheng－de，et al.Hierarchical self－assembly of DNA into symmetric supramolecular polyhedral[J].Nature，2008，452：198－202.

[16] WINFREE E.Design and self－assembly of two－dimensional DNA crystals[J].Nature，1998，394：1223－1226.

[17] YURIY B.Solving NP－complete problems in the tile assembly model[J].Theoretical Computer Science，2008，395（1）：31－46.

[18] 李肯立，姚凤娟，许进，等.子集和问题的O（1.414n）链数DNA计算机算法[J].计算机学报，2007，30（11）：1948－1953.LI Ken－li，YAO Feng－juan，XU Jin，et al.An O（1.414n）volume molecular solutions for the subset－sum problem on DNA－based supercomputing [J].Chinese Journal of Computers，2007，30（11）：1948－1953.（In Chinese）