带加劲肋钢－混凝土组合蜂窝梁力学性能试验研究＊

王皓磊，邵旭东†，刘 春，余加勇

（1.湖南大学 土木工程学院，湖南 长沙 410082； 2.广东省公路建设有限公司，广东 广州 510000）

带加劲肋钢－混凝土组合蜂窝梁是一种新型的桥梁结构形式[1]，箱梁腹板成排开孔，结构通透，造型新颖，抗弯刚度大于扩张前截面，截面效率高；采用圆形孔，避免孔角较大的应力集中[2－3]；在孔洞间设置竖向加劲肋，能有效地防止腹板的失稳[4]，提高其承载能力.

1951年美国德克萨斯州公路局曾将蜂窝钢梁作为两座简支梁桥的主梁，其跨度分别为100英尺和65英尺[5]，这也是至今仅有的将蜂窝梁结构应用于桥梁工程的记录.国内外对腹板开孔结构的研究多针对于蜂窝钢梁[3，6－7]和腹板开单孔的组合梁[4]，较少涉及组合蜂窝梁[8]，而对于带加劲肋组合蜂窝梁这一结构形式则鲜有报道[2]，这限制了其在实际工程中的应用.

钢－混凝土组合蜂窝梁结构腹板成排开孔，剪力的传递不连续，从而造成其受力和变形性能有别于常规组合结构.本文根据普通钢－混凝土组合梁实桥按1∶10的比例，按照几何相似、边界条件相似、物理参数相似的等效原则设计制作了一根组合蜂窝梁的缩尺模型，并进行了静载试验，考察其受力和变形等基本力学性能.以空腹桁架简化理论为基础，推导了组合蜂窝梁应力和变形的计算公式，通过理论和试验结果的对比分析，验证计算方法，进一步探明了这种新型组合结构的受力性能，为该结构的实际应用奠定基础.

1 试验概况

1.1 试验模型和材料特性

试验梁长11 382mm，宽1 200mm，高530 mm，其中钢箱梁高500mm，钢腹板厚3mm，中支点两侧5 214mm范围内腹板变厚度为5mm，底板宽600mm，厚4mm，混凝土板宽1 200mm，厚40 mm，承托高40mm；在钢主梁腹板处沿纵向开设一系列圆孔，文献[1]中拟定的相关尺寸：圆孔半径为116mm，间距为334mm，共计33个，相邻圆孔之间实腹板上焊接竖向加劲肋，以增强其稳定性；混凝土板与钢箱梁的连接采用开孔板剪力件，沿试验梁纵向在钢腹板上端布置抗剪结合销圆孔，圆孔中贯穿Ф8钢筋与混凝土隼结合；钢梁底板根据稳定性要求焊接纵向加劲肋.试验梁构造如图1所示.

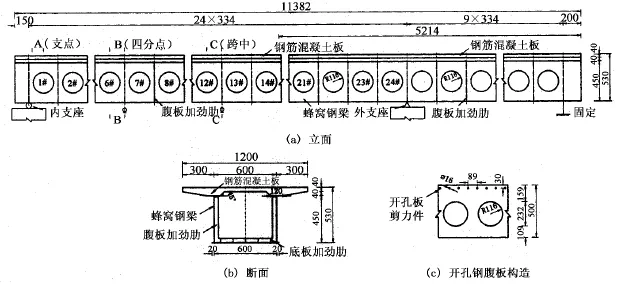
图1 钢－混凝土组合蜂窝梁试验模型示意图（mm）Fig.1 Schematic drawing of steel－concrete composite castellated beam／mm

试验梁钢构件在工厂内制作焊接，钢构件完成后运送至试验室，支模、绑扎普通钢筋、安装开孔板剪力连接件的贯穿钢筋，最后浇注混凝土，养护至28d龄期.试验梁制作情况如图2所示.

模型制作的同时，预留材料，根据标准方法进行材性试验，各材料的力学性能如表1所示.

混凝土立方体抗压强度fcu＝33.5MPa，弹性模量Ec＝3.49×104MPa.

表1 钢板、普通钢筋力学性能Tab.1 Material properties of test specimen

图2 试验模型构造Fig.2 Construction of test specimen

1.2 加载与测试

钢－混凝土组合蜂窝梁静载试验分为两个工况，如图3和图4所示，分别为：

工况1 集中加载，在试验梁长跨三分点位置施加两点集中荷载，并用分配横梁分载至腹板位置处，利用反力架和手摇千斤顶为主要加载装置，压力传感器读取实际荷载数值，分7级加载，每级加载量为5kN；

工况2 均布加载，在试验梁长跨通过装载砝码的铁篮施加均布荷载，分两级加载，每级2.5kN／m取跨中、四分点和支点截面为测试断面，测点布置如图5所示.在测试断面箱梁底板布设百分表，测得其竖向挠度，采用人工读数；在测试断面顶底板及腹板布置电阻应变片，采用TDS－602数据采集系统进行数据采集.

图3 工况1加载示意图Fig.3 Test setup of loading condition 1

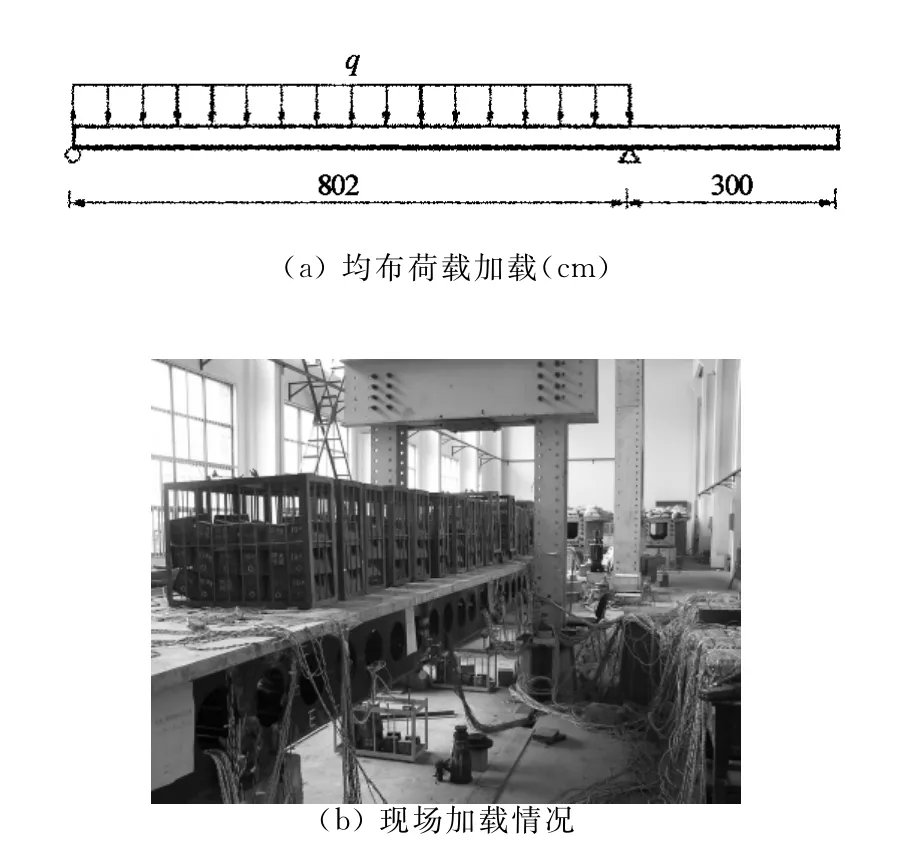
图4 工况2加载示意图Fig.4 Test setup of loading condition 2

图5 测点布置示意图Fig.5 Distribution of test measured points

2 应力计算

采用费氏空腹桁架简化理论计算组合蜂窝梁的应力，将组合蜂窝梁视为刚结点桁架，认为：由剪力引起的弯矩其反弯点出现在每个孔洞的垂直中心线上；作用于开孔截面处的剪力，在上、下T截面中分配，大多数情况下，下T截面承担了10%～40%的截面总剪力，而对于非对称的截面，下T截面所承担截面总剪力的比例可取为40%[4].假定组合蜂窝梁的混凝土板和钢梁之间有可靠的连接，弹性阶段内忽略组合梁的相对滑移，按换算截面法将钢和混凝土等效成同一种匀质材料进行计算.

如图6和图7所示，以圆孔圆心处垂直轴线为中心，与垂直中心线成φ角的斜截面为计算截面.组合蜂窝梁在弯矩M和剪力V的共同作用下，开孔截面上、下T处的作用力可分解为轴力Nφ、剪力Vφ和弯矩Mφ.假定孔洞中心截面处上T截面承担的总剪力百分比为α，下T截面为（1－α），依据截面分力法，孔洞中心截面的内力可表示为：

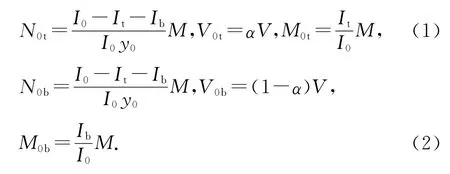
式中：下标t，b分别代表上、下T截面；y0为上、下T截面中性轴之间的距离；I0，It，Ib分别为孔洞中心截面、上T截面、下T截面的惯性矩.

随角度φ的变化，可分4种情况考虑计算截面的受力状态：

图6 组合蜂窝梁计算截面Fig.6 Calculating section of composite castellated beam

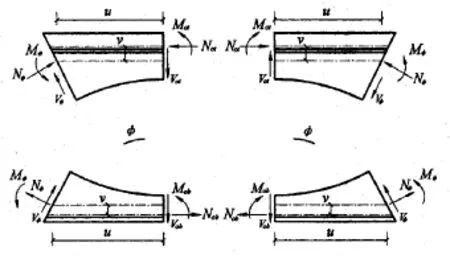
图7 组合蜂窝梁应力计算模型Fig.7 Stress calculation model

1）当0≤φ＜arctan[（lr－tr／2）／（R＋ht]时，加劲肋不参与受力计算；

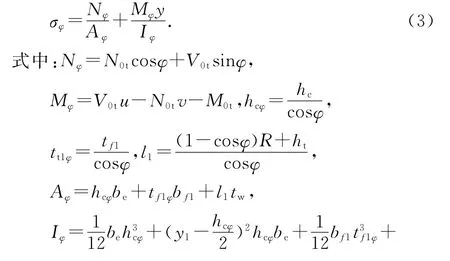
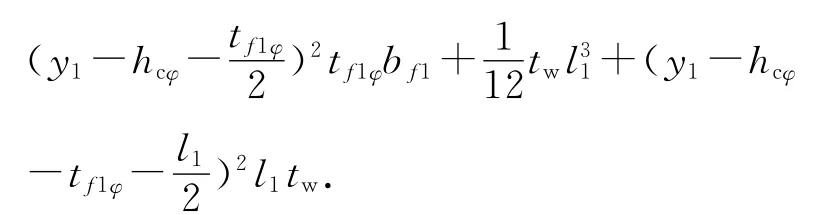
式中：Aφ为夹角为φ的计算截面面积；Iφ为夹角为φ的计算截面惯性矩；y1为计算截面形心至截面上缘距离；y为计算截面形心至计算位置的距离.

2）当arctan[（lr－tr／2）／（R＋ht）]≤φ＜π／2时，加劲肋和混凝土板均参与受力计算，且不考虑周围圆孔对计算截面的折减；

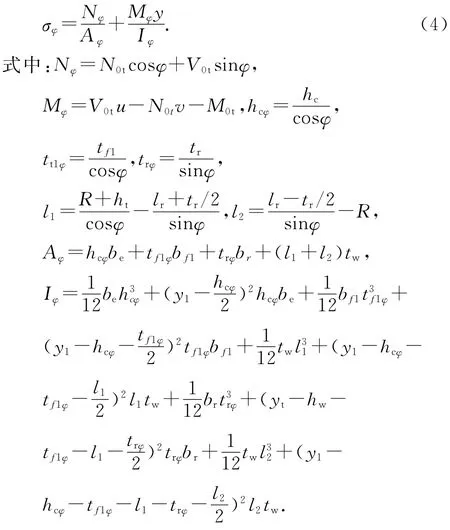
当π／2≤φ＜π－arctan[（lr－tr／2）／（R＋hb）]时和π－arctan[（lr－tr／2）／（R＋hb）]≤φ＜π时，混凝土板均不参与受力计算；公式推导过程与上述类似，在此不再赘述.

3 挠度计算

组合蜂窝梁的挠度也可以运用费氏空腹桁架比拟法来计算，其挠度表达式包含弯曲挠度、剪切挠度和剪力次弯矩引起的挠度3部分，计算公式为：

式中：fm为弯曲挠度；fv为剪切挠度；fvm为剪力次弯矩引起的挠度.

1）fm的计算 .如图8所示，为一组合蜂窝悬臂梁，长L，钢梁高hs，混凝土翼缘厚hc，有效宽度bc，开孔直径d，开孔间距e，空洞数为n，将圆孔简化为d×d的矩形孔（虚线），实腹截面和空腹截面的刚度分别为EIs和EI0.

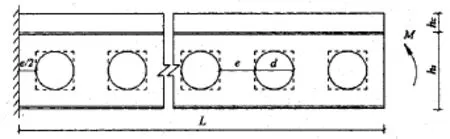
图8 纯弯作用下组合蜂窝梁Fig.8 Composite castellated beam under pure bending

设悬臂梁端作用有一弯矩M，将组合蜂窝梁视为经典梁，其相应的刚度为EIeff，悬臂端转角可表示为：

另一方面，根据虚功原理，当L足够大时，组合蜂窝梁悬臂端转角为：

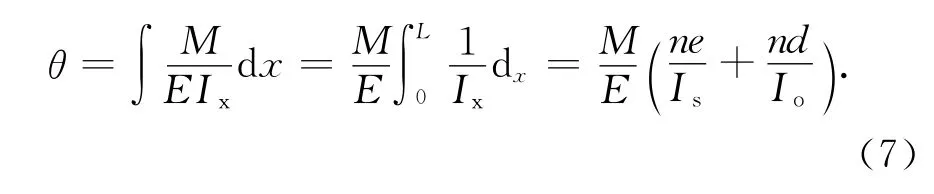
由式（6）和式（7）可得等效惯性矩：

则弯曲挠度fm可按下式计算：

式中：Is为实腹截面惯性矩；In为空腹截面惯性矩；fsm为当量实腹梁弯曲挠度.

2）fv的计算 .与fm的计算类似，如图8所示，利用剪切挠度计算公式，可以得到剪切挠度的计算公式：

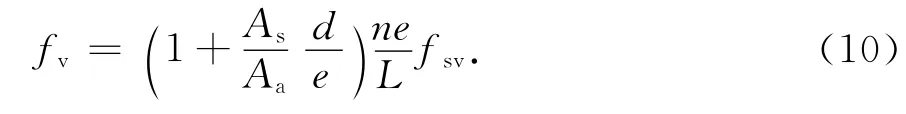
式中：As为实腹截面面积；Aa为空腹截面面积；fsv为当量实腹梁剪切挠度；kv为截面形状系数；kv＝；S为截面面积矩；b为截面宽度；其余参数同式（9）.

3）fvm的计算.如图9所示，取组合蜂窝梁一个孔单元为分析对象，按照费氏空腹桁架比拟法的假定，对每一孔单元，剪力次弯矩引起的挠度fvm为梁桥在剪力作用下的弯曲变形和由墩转动所产生的变形叠加而成.设孔单元i上作用有剪力Vi，Vi在空腹截面的分配系数为α，即空腹上、下T所分配的剪力分别为αVi，（1－α）Vi.利用图乘法可得孔单元i剪力次弯矩挠度的表达式：

式中：V为孔单元i上作用的剪力；It，Ib分别为上、下T桥截面惯性矩；Id为墩截面惯性矩，Id＝k′twe3，k′为 刚 度 加 强 系 数，对 于 圆 孔 截 面，k′＝14[7]；α为剪力在上、下T截面的分配系数，α可取为0.6[4]；l0为桥跨长度，l0＝ξd，ξ为形状系数，对圆孔截面可取为0.68[7]；其余各参数同图9所示.

图9 组合蜂窝梁剪力次弯矩挠度计算简图Fig.9 Calculation sketch of deflection induced by shear－secondary bending

对于组合蜂窝梁的跨中，剪力次弯矩挠度为：

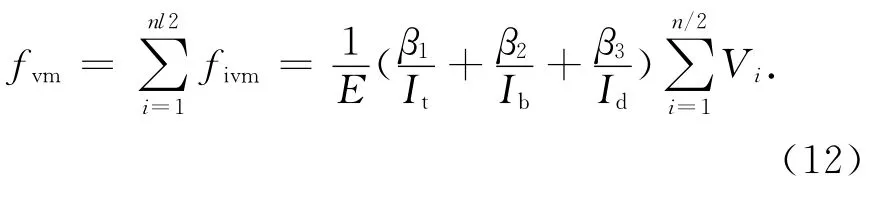
4 结果对比分析

4.1 应力分布

试验梁圆孔周边应力实测值如表2和表3所示，理论计算结果如图10所示.

由表2、表3和图10可知：1）应力沿圆孔边缘不均匀分布，在φ＝45°，135°，225°和315°时应力较大；试验梁跨中截面C下翼缘板的应力分别为：35.49MPa（工况1，40.8kN）和21.04MPa（工况2，5kN／m），均要小于孔口的应力值，说明圆孔边缘要先于翼缘达到材料屈服.2）弯剪共同作用下，采用理论方法计算得到环向应力与实测值分布规律基本一致，两种工况计算最大值分别为：36.38MPa（工况1，B截面φ＝155°）和21.47MPa（工况2，B截面φ＝160°），实测值则分别为42.32MPa和21.22MPa，均在φ＝135°测得，说明φ＝135°～165°的截面为应力相对集中的区域；而在纯弯段，截面C的应力沿圆孔中心线对称分布.3）孔洞中心φ＝0°和φ＝90°截面处环向应力的理论值和试验值差别较大，这是因为简化计算中孔洞垂直中线假设为反弯点，且不计周围孔洞的折减，使得计算存在较大误差.

图10 圆孔环向应力分布图／MPa，拉＋压－Fig.10 Stress distribution of holes／Mpa，tensile＋compressive－

4.2 挠度

由式（5）～式（12）计算得到试验梁跨中截面挠度，并与相同尺寸的实腹梁进行比较，表4给出了两种工况下最后一级荷载时的计算结果.由表4可以看出，组合梁的挠度由弯曲挠度、剪切挠度和剪力次弯矩挠度组成，外荷载不同，各部分所占比例也不尽相同.工况1时，弯曲挠度约为总挠度的79%，剪切挠度为6%，剪力次弯矩挠度为15%，可见组合蜂窝梁中，剪力次弯矩对变形的影响不可忽略.工况2时，主要以弯曲挠度为主，其约占总挠度的90%，剪切挠度和剪力次弯矩挠度分别约为7%和3%.与相同尺寸的实腹梁相比，不同工况下组合蜂窝梁在跨中的挠度增大了约20%（工况1）和14%（工况2）.

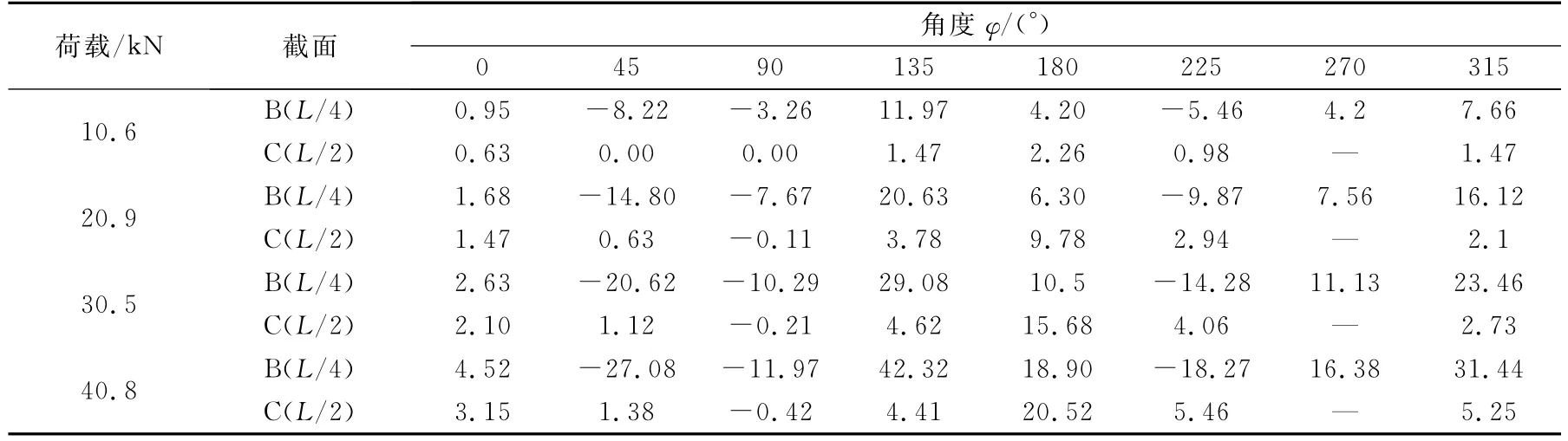
表2 （工况1）圆孔环向应力实测值（拉＋压－）Tab.2 Experimental results of stress for holes（loading condition 1），tensile＋ compressive－ MPa

表3 （工况2）圆孔环向应力实测值（拉＋压－）Tab.3 Experimental results of stress for holes（loading condition 2），tensile＋ compressive－ MPa

表4 跨中挠度计算结果Tab.4 Theoretical results of deflection

将试验值、理论计算值和有限元值一并列于表5～表6中.此外，多数国家规范中采用估算方法计算蜂窝梁结构的挠度，如日本规范中将其取为1.2～1.25倍相同尺寸实腹梁的计算挠度[9]，将此计算结果也列于表中.

由表5～表6可知，各加载工况下式（5）的计算值与试验值、有限元值吻合良好，但多数高于试验值，这是因为式（5）的计算中将圆孔简化为方孔，增大了削弱面积，并且没有考虑纵横向加劲肋对梁刚度的贡献，总体偏于安全，式（5）值与试验值的误差在10%以内，其精度稍高于日本规范计算值，能满足实际工程的要求.

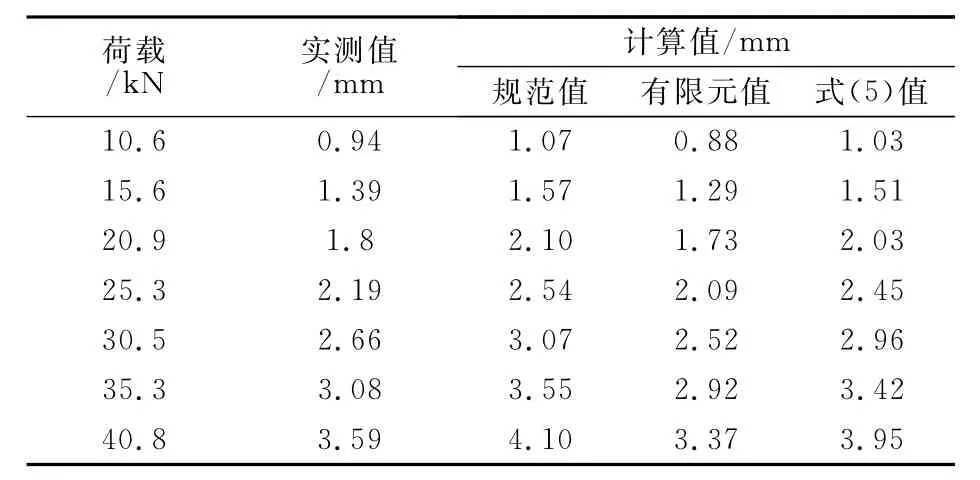
表5 跨中挠度实测值与计算值比较 （工况1）Tab.5 Comparison results of deflection（loading condition 1）

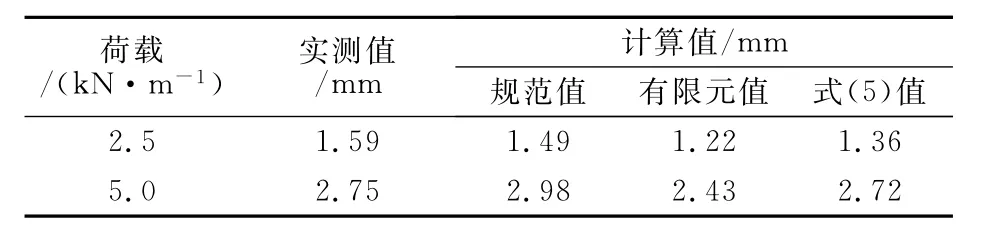
表6 跨中挠度实测值与计算值比较 （工况2）Tab.6 Comparison results of deflection（loading condition 2）

5 结 语

1）基于费氏空腹桁架理论的应力计算方法能较准确地计算出钢－混凝土组合蜂窝梁圆孔边缘最大环向应力的位置及大小，且能较好地计算出其他各点环向应力分布规律和趋势，该方法适用于组合蜂窝梁弹性阶段的强度分析.

2）钢－混凝土组合蜂窝梁腹板圆孔的环向应力分布十分不均匀，分布规律比较复杂.弯剪共同作用下，圆孔最大环向应力出现在φ＝150°～165°截面处，并与其相对应的圆环位置形成4个应力峰值区，压应力区和拉应力区交替分布，随着荷载的增加，这4个区域会率先进入弹塑性阶段，并且压应力区域存在局部稳定问题，在设计中应引起足够重视.

3）基于费氏空腹桁架理论的挠度计算方法能满足实际工程的要求，得到的计算结果与有限元结果、试验结果吻合良好，对比误差基本上在10%以内，且总体偏于保守，可供实际工程设计参考.

[1] 湖南大学.钢－混组合结构的双层连续梁桥[P].中国：ZL 2007 1 0192479.3，2009－09－23.Hunan University.Steel－concrete composite double－decker continuous bridge[P].China：ZL 2007 1 0192479.3，2009－09－23.（In Chinese）

[2] 邵旭东，刘俊珂.计入加劲肋的圆孔蜂窝组合梁强度简化计算[J].湖南大学学报：自然科学版，2009，36（9）：7－11.SHAO Xu－dong，LIU Jun－ke.Reduced computation of the strength of circular hole castellated composite beams with stiffened webs[J].Journal of Hunan University：Natural Sciences，2009，36（9）：7－11.（In Chinese）

[3] 邹锦华，魏德敏，苏益声，等.蜂窝梁的简化计算及其试验对比[J].华南理工大学学报，2005，33（1）：47－51.ZOU Jin－hua，WEI De－min，SU Yi－sheng，etal.Reduced calculation and its experimental comparison for castellated beams[J].Journal of South China University of Technology，2005，33（1）：47－51.（In Chinese）

[4] LAWSON R M，LIM J，HICKS S J，etal.Design of composite asymmetric cellular beams and beams with large web openings[J].Journal of Constructional Steel Research，2006，62：614－629.

[5] 汤庆轩.简支蜂窝梁整体稳定的研究[D].北京：中冶集团建筑研究总院，2004：1－11.TANG Qing－xuan.Study on overall stability of simply supported castellated beam [D].Beijing：Central research institute of building and construction，2004：1－11.（In Chinese）

[6] KOLOSOWSKI J.Stresses and deflection in castellated beam[J].The Structural Engineer，1964，42（1）：19－24.

[7] 郑坤龙.变高度工字截面圆孔蜂窝梁的挠度计算[D].长沙：中南大学土木工程学院，2007：1－66.ZHEN Kun－long.Deflection calculation of tapered castellated beams[D].Changsha：College of Civil Engineering，Central South University，2007：1－66.（In Chinese）

[8] 薛桂玉，徐德新.钢与混凝土蜂窝形组合梁设计中的若干问题[J].建筑结构学报，1999，20（4）：18－24.XUE Gui－yu，XU De－xin.Some supplemental recommendation for design of steel and concrete castellated composite beam[J].Journal of Building Structures，1999，20（4）：18－24.（In Chinese）

[9] 何一民，李鹏鸿，于力.蜂窝梁挠度的实用计算方法[J].工业建筑，1994（8）：9－15.HE Yi－min，LI Peng－hong，YU Li.The applicable method for the deflection calculation of castellated beams[J].Industrial Construction，1994（8）：9－15.（In Chinese）