高层钢管混凝土结构施工全过程数值模拟

刘 俊，吴 杰，罗晓群，崔晓强，张其林

（1.同济大学 土木工程学院，上海200092；2.上海建工集团 上海200050）

建筑结构设计通常是以完整结构作为设计对象的。然而实际结构是在经历了整个施工建造过程后成型的。在这个过程中结构从无到有、材料性能也随时间发生着变化。对于多层建筑，该区别造成的影响不是很大，可不考虑。但高层建筑对微小变形十分敏感，稍有不慎便可能引起内力过大，甚至造成结构破坏。所以，高层结构设计必须进行施工过程分析。施工过程分析属于慢速时变结构力学的范畴，可以忽略动力效应而采用时间冻结法进行处理［1］。但必须考虑2方面的时变效应：一是材料的收缩徐变、弹性模量和强度随施工过程（时间）发生变化（主要针对混凝土）［2－3］；二是结构形状（刚度）随施工过程发生变化。由于这2方面的时变效应，高层结构的实际受力状态与基于完整结构的设计结果相比会有较大差异［4－10］，忽略这样的差异将会导致设计结果不安全。

高层结构中广泛采用的钢管混凝土构件是由钢材和混凝土两种材料组成的，两者共同工作。对钢管混凝土组合构件进行时变分析时必须考虑核心混凝土时变特性对构件的影响，实现该模拟比较困难。笔者提出了分别考虑混凝土材料和钢材、通过导入主从节点约束使两者共同工作的钢管混凝土组合构件分析模型，可以精确考虑混凝土材料的收缩徐变及其对组合构件的作用效应，在此基础上提出了高层钢管混凝土结构的施工全过程数值分析方法。

1 施工过程分析原理

完全模拟施工过程是比较困难的，很多学者提出了基于不同假定的施工过程近似模拟方法［11－12］。文献［7］中提出的近似模拟施工过程的方法在中国的高层结构设计软件中广泛应用。但该方法是取全结构的刚度来计算，与实际施工过程的变结构变刚度情况不符。笔者采用了比较接近施工实际的模拟施工过程方法。把1个m层框架的荷载效应分析看作是包含m个子结构的荷载效应分析，子结构层数由1～m连续变化，每个子结构只承受相应的顶层荷载。第i层的荷载效应是第i～m个子结构中该层荷载效应的叠加。该方法与一般分析的区别见图1和图2［13］。

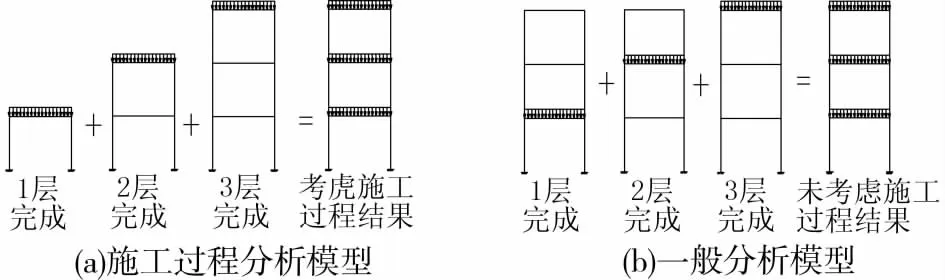
图1 分析模型

图2 分析结果

考虑施工过程的分析结果是考虑了结构随施工进度变化和施工找平影响的叠加结果，如图2（a）所示。施工步骤1）1层受单位荷载后的位移为1，2、3层由于未被激活，对应位移为0；2）将第2层建造到设计标高，受荷后，1层新增位移为1，2层位移为2，3层由于未被激活，对应位移为0；按上述过程完成第3步，将各层位移叠加得到最终位移值。一般分析结果见图2（b）：单位荷载作用在第1层时，由于3层构件同时处于激活状态，所以每层位移均为1；单位荷载作用在第2、3层产生的位移及叠加后的总位移如图2（b）所示。由2图分析结果的差异可以看出分析时考虑施工过程的重要性。

2 混凝土时变模型

徐变是混凝土在持续荷载作用下的非弹性变形，它对静定结构和组合结构有着重要影响。通常结构最终的徐变量可达到弹性变形量的2～3倍，因此混凝土时变特性对结构的影响将是巨大的。在施工过程分析时，材料的时变模型是要首先确定的，它直接影响到施工过程分析的准确性。笔者以CEB－FIP MC90的时变模型作为计算依据，采用按龄期调整的有效模量法（AEMM法）建立了混凝土时变模型。

2.1 混凝土收缩徐变模型

CEB－FIP MC90中混凝土收缩应变表达式为

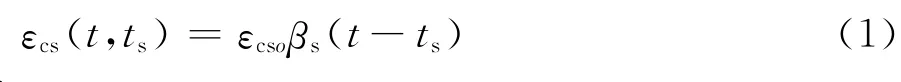
式中：εcs为收缩应变；ts为开始考虑混凝土收缩时的龄期；εcso为名义收缩系数；βs为收缩随时间发展的系数。

CEB－FIP MC90中混凝土徐变应变表达式为

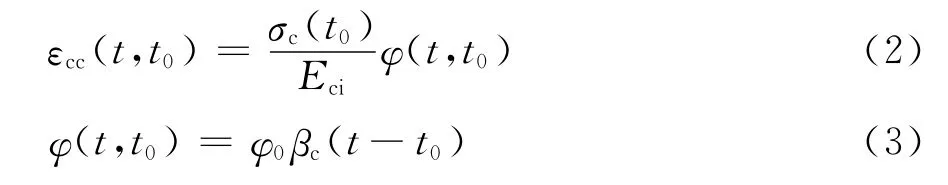
式中：εcc为徐变应变；t0为开始加载时的混凝土龄期；Eci为28d龄期的混凝土弹性模量；φ为徐变系数；φ0为名义徐变系数；βc为加载后徐变随时间发展的系数。

2.2 按龄期调整的有效模量法（AEMM）

在叠加原理和线性徐变假设条件下，总应变可表示为式（4）［14］。

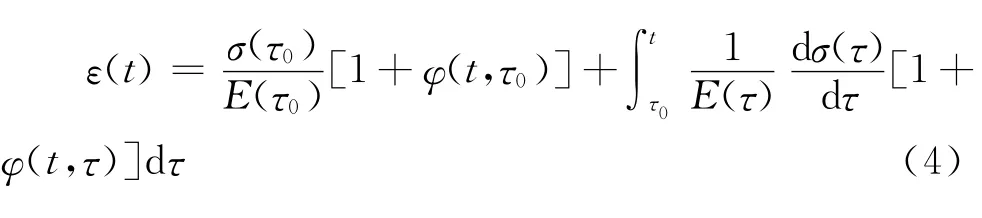
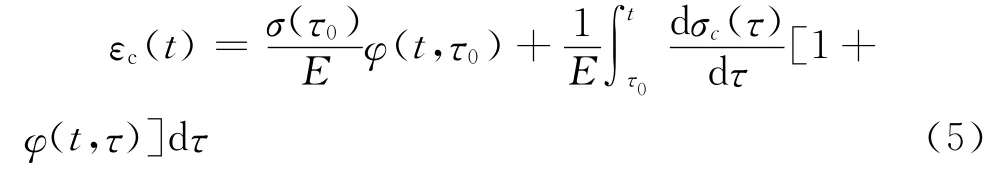
应用中值定理，引入老化系数ρ（t，τ0），令Eφ＝为按龄期调整的有效模量，可得到式（6）。

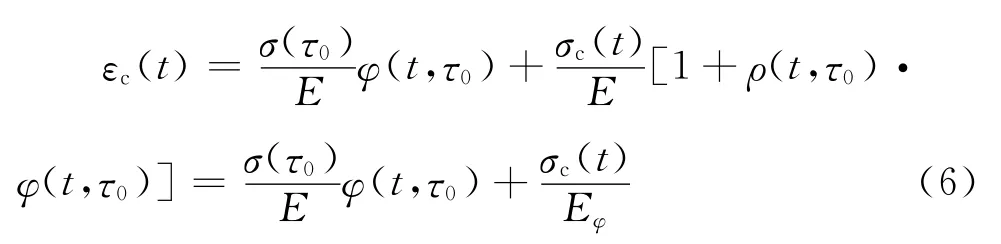
按龄期调整有效模量法就是用老化系数来考虑混凝土老化对最终徐变值的影响，实质是用积分中值定理将徐变计算的积分方程转化为代数方程。

3 钢管混凝土时变模型

3.1 基本假定

在钢管混凝土的2种材料共同工作时，钢管和核心混凝土都处于多向应力状态。在核心混凝土收缩徐变的同时，钢管和混凝土内的应力相互影响。因此，钢管混凝土的受力分析将是一个复杂问题［15］。为简化计算，作如下基本假定：1）混凝土与钢管之间粘结可靠，协同工作；2）忽略钢管与混凝土的径向作用力，核心混凝土按单轴受力分析；3）由于钢管阻止了核心混凝土水分的丧失，所以其收缩可以忽略。基于上述原理和假设，可以建立钢管混凝土徐变模型［16］。

3.2 钢管混凝土轴心受压构件的徐变计算模型

考虑钢管与核心混凝土共同工作，当在无新的外力作用时，核心混凝土产生徐变，钢管混凝土截面产生体系内应力重分布。当核心混凝土产生自由徐变应变为核心混凝土产生徐变后钢管的应变增量，为钢管和混凝土的协同变形引起的核心混凝土轴向应变恢复量，可得到式（7）。

因此，产生徐变后钢管的应变增量即为钢管混凝土的实际徐变应变，如式（8）所示。

由于忽略钢管与核心混凝土的径向作用力，则

设核心混凝土初始应力为σ0，则发生徐变后时间t时的应力如式（11）。

在时间为t时，钢管混凝土上产生的徐变等于当时核心混凝土上作用的应力与徐变度c的乘积，即

将式（8）、（10）、（11）代入式（12）得式（13）。

将式（13）带入式（10），由式（11）得式（14）。

设钢管混凝土初始应变为ε0，则可得到式（15）。

基于上述理论，将钢管混凝土用钢管和混凝土2个单元表示，并将2个单元的两端节点取为主从约束节点，以实现在考虑混凝土单元徐变的同时实现钢管单元和混凝土单元的协调工作。

3.3 基于构件时变模型的高层建筑数值模拟软件

基于上述徐变计算模型并结合有限元理论就可模拟徐变对钢管混凝土的影响。钢管混凝土柱徐变分析流程见图3。

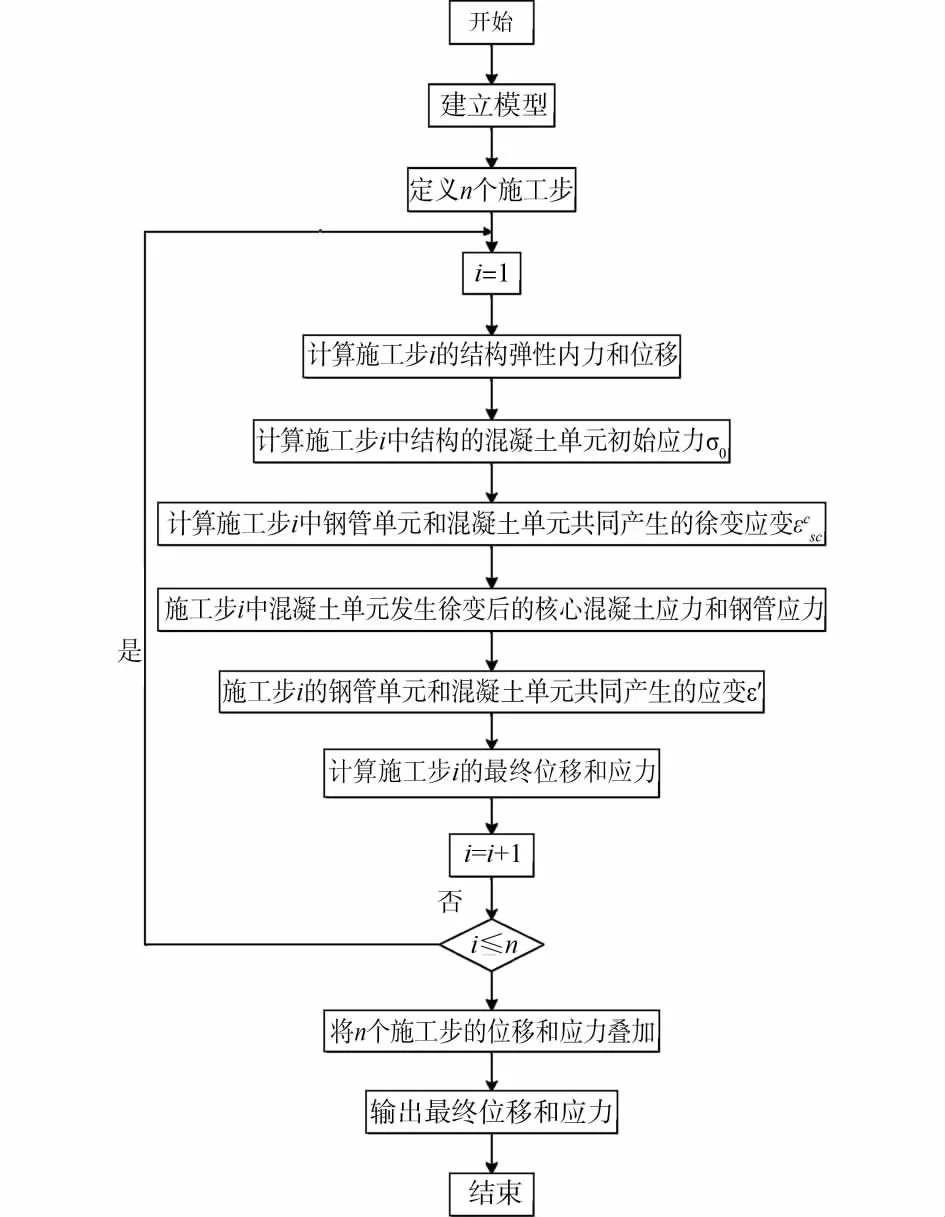
图3 钢管混凝土徐变分析流程图

在上述钢管混凝土徐变模型的基础上，以Visual C＋＋和ObjectARX为工具，研发了基于构件时变模型的高层建筑数值模拟软件。图4为软件架构图，图5为软件主界面。软件可实现施工过程数据的交互式输入、施工全过程的仿真分析、计算结果的图形显示和文本查询等功能。施工全过程数值模拟的具体流程见图6。

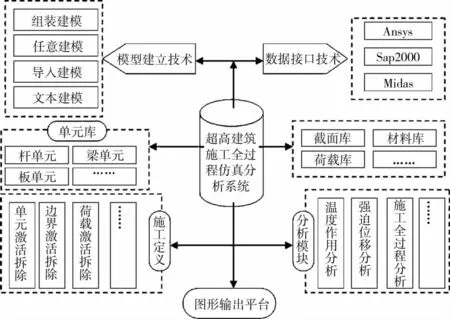
图4 软件架构图

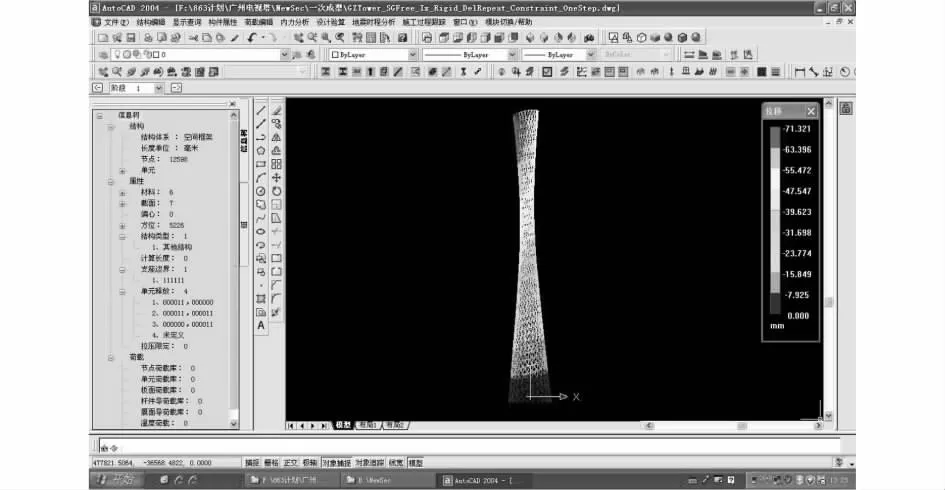
图5 主界面及各级菜单

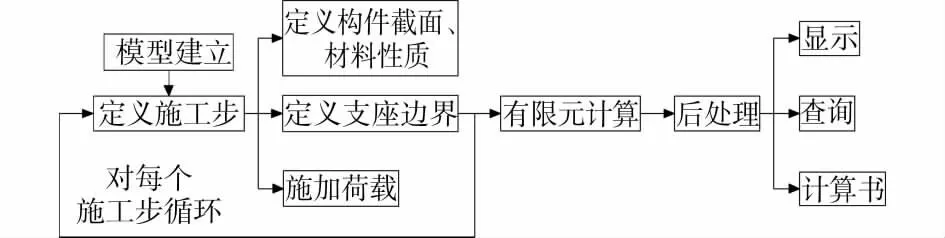
图6 施工过程模拟流程图

3.4 时变模型和模拟软件的数值验证

图7为一钢管混凝土柱施工过程示意图，柱直径500mm，钢管壁厚15mm，混凝土采用C40，钢管采用Q345，整个计算过程分3个工况：工况CS1、CS2持续30d，工况CS3持续180d，各工况受荷情况如图7所示。图8为2层平面钢管混凝土框架施工过程示意图，施工工况、柱尺寸和材料同图7中的钢管混凝土柱，框架梁采用300mm×600mm的矩形截面，C40混凝土，受荷情况如图8所示。为验证方法的正确性，将计算结果与Midas软件和桥梁博士软件作了对比分析。表1和表2分别为钢管混凝土柱和2层框架的计算结果，从表中可看出，计算结果基本一致，从而验证了方法的正确性。MIDAS徐变分析采用的是分时步徐变叠加法（SSM法），笔者和桥梁博士采用的是龄期调整有效模量法（AEMM法）。SSM法由于需要考虑应力历史，计算量较大；AEMM法相对来说计算量较小。

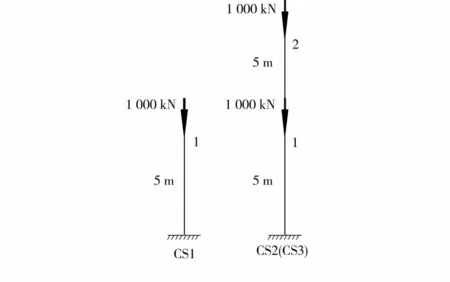
图7 钢管混凝土柱施工过程模型

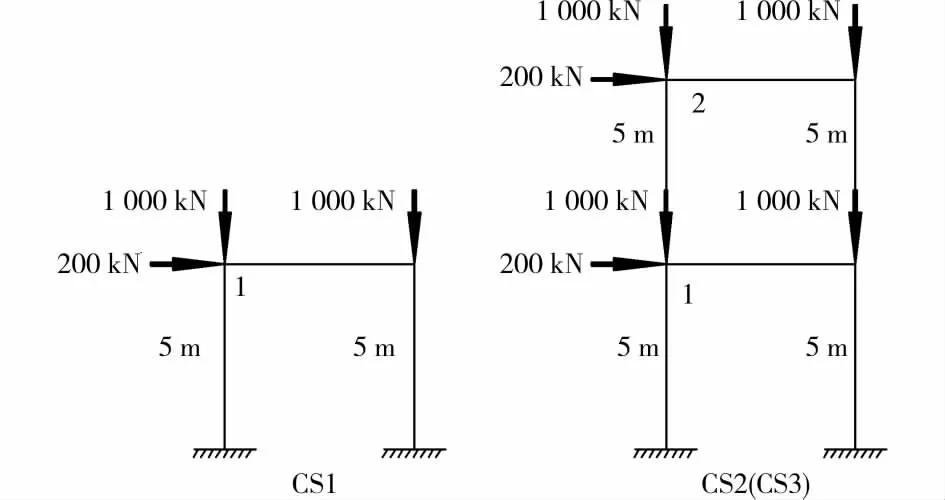
图8 2层钢管混凝土框架施工过程模型

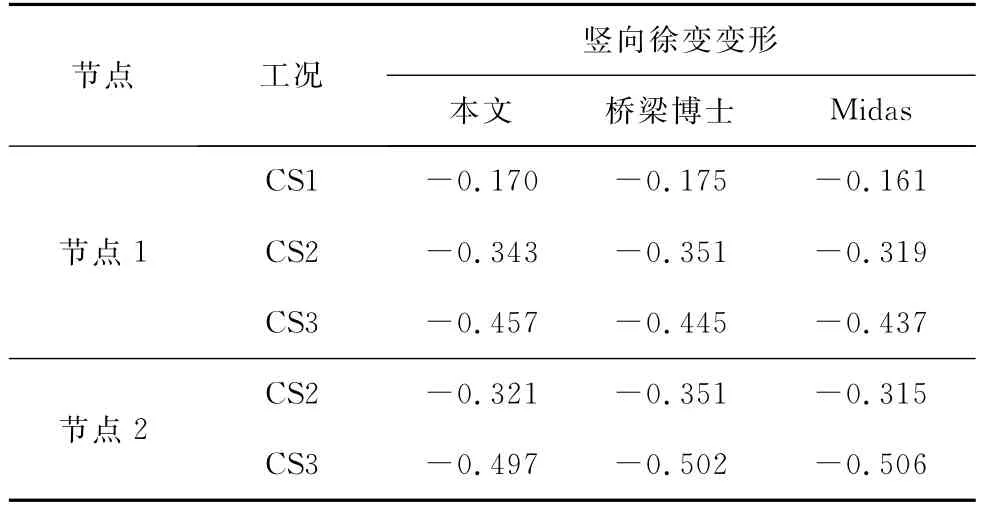
表1 钢管混凝土柱分析结果对比 mm

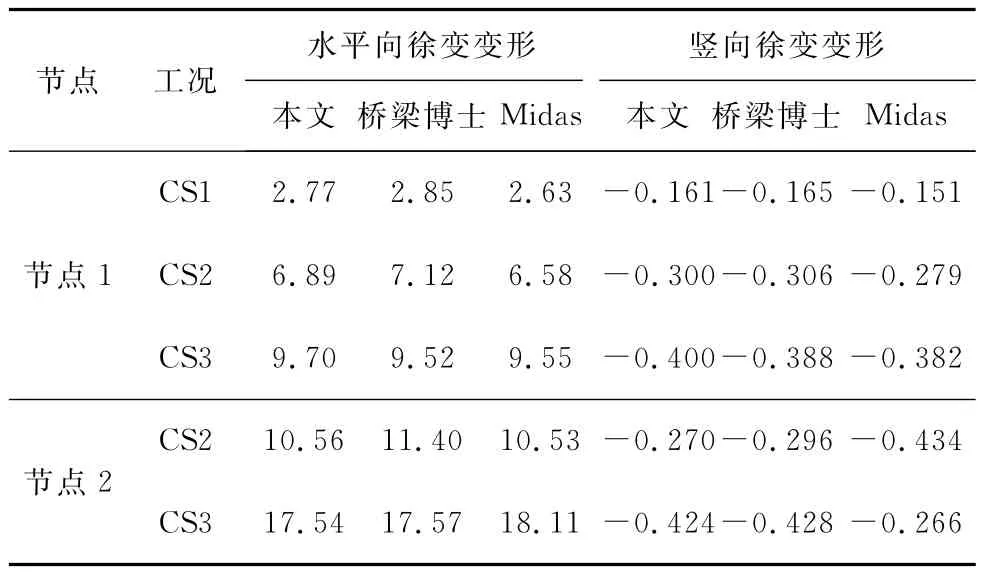
表2 2层平面钢管混凝土框架分析结果对比 mm

4 工程实例分析

4.1 工程概况

广州新电视塔位于广州市海珠区赤岗塔附近，塔高450m，天线桅杆高160m，总建筑面积114 054m2。广州新电视塔的结构体系为钢管混凝土外框筒和钢筋混凝土核心筒组成的混合结构体系。其结构由2个向上旋转的椭圆形变化生成，1个在基础平面，1个在450m高的平面上，2个椭圆彼此扭转135°，2个椭圆扭转在腰部收缩变细。结构布置形式不对称，构件在施工过程中受力状态复杂。因此，为确保建造完成的结构和设计目标一致以及工程在整个施工过程中的安全性，有必要对广州新电视塔进行施工过程分析。

4.2 计算模型

本节建立了广州新电视塔的整体三维有限元模型，见图9。钢管混凝土柱和钢梁采用梁单元，采用C60的混凝土和Q345的钢材。钢筋混凝土核心筒和楼板采用板单元，其中核心筒采用C60的混凝土，楼板采用C35的混凝土。所有截面尺寸按设计值取，见图10。

塔体的施工过程分析，按照施工流程，分析了50个工况。每个工况中结构主要包括：外框筒（由外环与柱组成）、混凝土核心筒和楼板。工况1为将核心筒施工至46.2m；工况2至工况39为每个工况将外框筒施工至一新环梁高度，同时核心筒向上施工8.4m，让外框筒和核心筒始终保持40m左右的高差，工况39时核心筒施工完毕；工况40至工况50为每个工况将外框筒施工至一新环梁高度，直至完工。在图11中简单列举一些施工工况。由于钢管混凝土的徐变早期发展很快，5个月后徐变曲线趋于水平，1a后徐变基本停止［17］。故本模型分析到施工完成后1 000d为止。

图9 实体模型

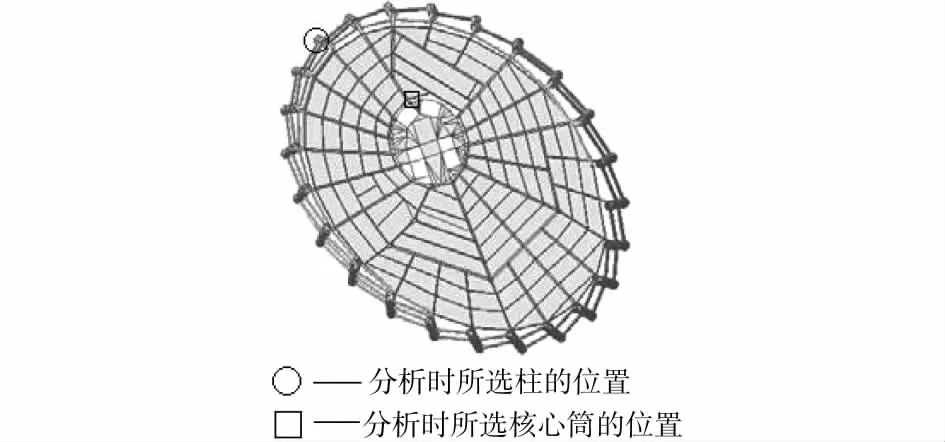
图10 结构分析位置

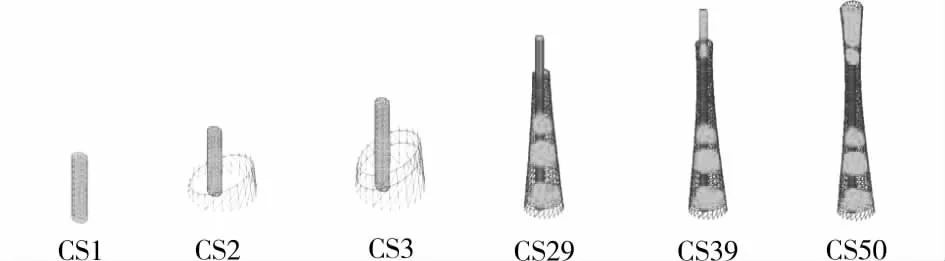
图11 施工工况

4.3 计算结果与分析

4.3.1 钢管混凝土柱竖向层间位移 图12分析数据对应于图10所示位置的钢管混凝土柱。由图12可知，考虑施工过程的分析结果与一般分析结果有很大差异。考虑施工过程的层间最大位移值发生在结构的中间部位，而一般分析的层间最大位移值发生在结构的最上部。考虑施工过程的位移曲线在后半段下降的原因是：笔者施工过程分析采用的是“分步建模技术”，即按施工步骤依次形成各施工阶段的结构刚度矩阵并施加相应荷载，未激活构件的刚度在整体刚度矩阵中并不出现，所以新激活构件的初始位移为0；针对该算例，相当于第i阶段的荷载对i＋1～n阶段新激活的构件不产生变形，这与实际施工情况是相符的。由图12（a）可见，施工刚完成时钢管混凝土柱的徐变变形始终小于弹性变形，最大的徐变变形和最大的弹性变形分别为4.85mm和22.83mm；施工完成后1 000d时（图12（b）），徐变变形有所增大，最大徐变变形为11.57mm。可见，钢管混凝土的徐变变形量相对于弹性变形量较小，但随着时间的增长徐变变形的影响会有所增大，应给予一定的考虑。

4.3.2 核心筒竖向层间位移 图13分析数据对应于图10所示位置的核心筒。由图13可知，核心混凝土的分析结果与钢管混凝土柱的结果有较大不同（此时收缩变形虽然存在，但收缩变形量相对于其他变形量微乎其微，故忽略不计）。核心筒混凝土的徐变变形量为弹性变形量的3倍左右。在施工完成时，见图13（a）。最大的徐变变形和最大的弹性变形分别为88.61、35.06mm。在施工完成后1 000d时，见图13（b）。最大徐变变形为116.11mm。可见，核心筒在施工过程分析时必须考虑混凝土的徐变，不然将导致分析结果误差太大。通过图12和图13还可以发现，各层层间变形值差异较大，为了使建成的实际结构与设计目标一致，应考虑逐层找平。

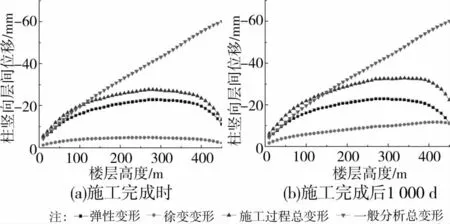
图12 钢管混凝土柱竖向层间位移曲线

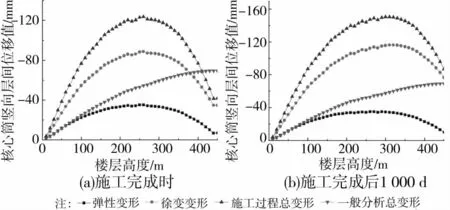
图13 核心筒竖向层间位移曲线

4.3.3 钢管混凝土柱与核心筒层间位移差 由图14可知，一般分析结果的层间位移差比较小，最大位移差为16.52mm，不考虑徐变的施工过程分析结果与一般分析结果较接近。而考虑徐变施工过程的层间位移差较大。施工完成时，最大位移差为96.35mm，发生在结构中部。在施工完成后1 000d时，在趋势相同的情况下差值进一步增大，最大位移差为117.98mm。可见，荷载长期效应的影响十分大（该长期效应包括施工工期内的）。若不采取必要措施，柱与核心筒之间的楼板在如此大的位移差的影响下必将破坏。这对施工找平提出了要求，既要使施工完成后的结构符合验收标准，又要考虑验收后荷载长期效应的影响，应引起足够重视。

4.3.4 核心筒实测数据与数值模拟数据的对比

对结构进行施工过程分析的同时，对结构进行了施工现场实测。传感器的布置图见图15，传感器在核心筒的布置图见图16。图17为测点1在传感器3方向从工况29到工况38的实测应变值推得的应力值，并将其与分析结果对比。可知，实测值比模拟数值小。而造成这种差异的原因较多，主要有以下几点：

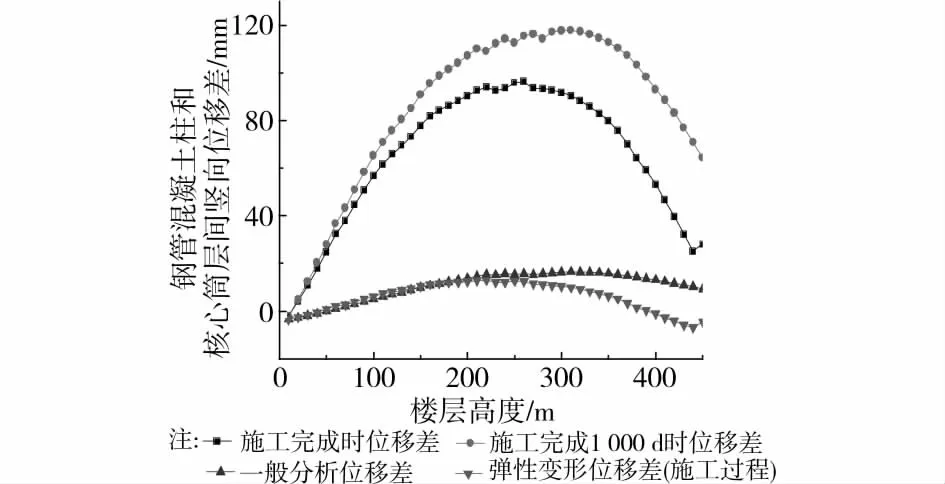
图14 钢管混凝土柱核心筒层间位移差曲线

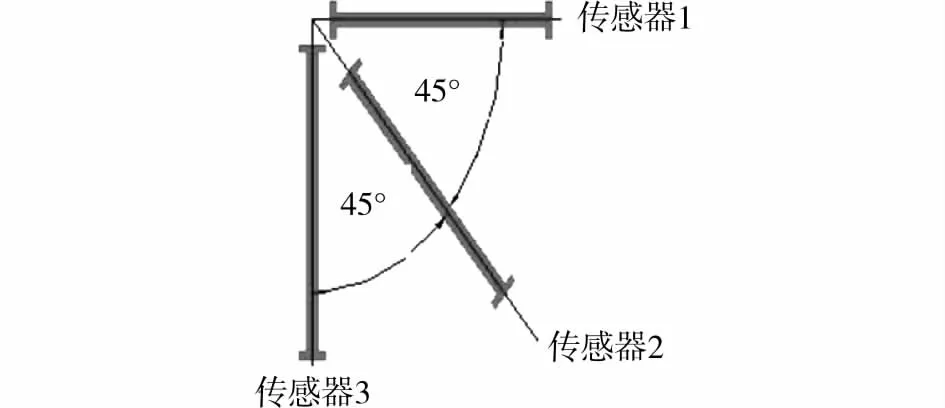
图15 应变花三向传感器布置图

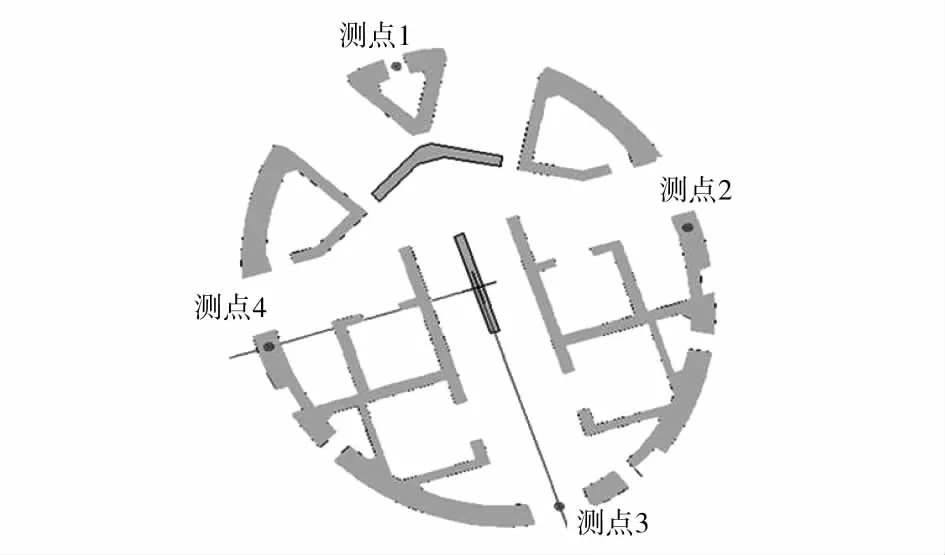
图16 核心筒应变花测点布置图

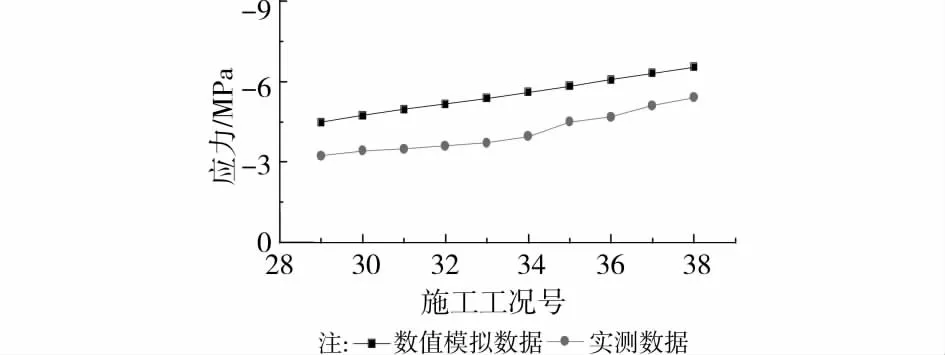
图17 核心筒应力时程曲线

1）荷载误差：由于实际施工荷载十分复杂，带有一定的随机性，与计算分析时的取值不会完全一致。

2）测量误差：由于采用振弦式应变计，外界环境振动对实测值会造成一定影响。

3）模型失真：实际核心筒含有大量构造配筋，而在分析时将其简化为单一混凝土材料，造成实测值比模拟值小。

5 结 论

1）提出了按主从节点约束考虑钢管与混凝土共同工作的钢管混凝土时变分析模型，基于该模型研制了高层钢管混凝土结构施工全过程的数值模拟软件，算例表明软件具有较好的适用性。

2）收缩徐变使高层建筑结构产生较大的竖向变形，必须对结构进行考虑收缩徐变的施工过程分析。相对于混凝土结构构件，钢管混凝土结构构件的徐变变形较小，但仍应给予考虑，否则计算结果误差较大。

3）数值计算结果表明钢管混凝土柱和核心筒的竖向位移差很大。该差值会引起较大的附加弯矩和附加剪力，在实际工程设计中应尽量考虑该影响。

4）为实现设计目标和保证长期使用安全，高层建筑施工时对结构应进行逐层找平，并应考虑到荷载长期效应对结构的影响。

［1］王光远.论时变结构力学［J］.土木工程学报，2000，33（6）：105－108.WANG Guangyuan.On mechanics of time－varying structures［J］.China Civil Engineering Journal，2000，33（6）：105－108.

［2］Kim J K，Han S H，Park Y D.Material properties of self－flowing concrete［J］.Journal of Materials in Civil Engineering，2008，9（11）：244－248.

［3］Altoubat S A，Lange A D.Creep，shrinkage，and cracking of restrained concrete at early age ［J］.Materials Journal，2006，98（4）：345－353.

［4］方辉，沈蒲生.高层框架考虑施工过程和徐变收缩影响的受力分析［J］.工程力学，2007，24（7）：94－98.FANG Hui，SHEN Pusheng.Analysis of high－rise frame structures with construction process，creep and shrinkage effects［J］.Engineering Mechanics，2007，24（7）：94－98.

［5］孙华华，赵昕，丁洁民，等.复杂钢框架核心筒连体高层建筑施工过程分析［J］.建筑结构，2009，39：221－224.SUN Huahua，ZHAO Xin，DING Jiemin，et al.Construction sequence analysis of skybridge connected complex steel frame core－wall tall building［J］.Building Structure，2009，39：221－224.

［6］Hong D K，Willam K，Shing B，et al.Failure analysis of R／C columns using a triaxial concrete model ［J］.Computers＆Structures，2007，77（5）：423－440.

［7］Coronelli D，Gabriella M M.Modeling of shear behavior in reinforced concrete beams ［J］.ACI Structural Journal，2006，103（3）：372－382.

［8］Mazzotti C，Savoia M.Experimental study of nonlinear creep of concrete at high stress level［J］.ACI Structural Journal，2006，103（2）：259－264.

［9］Sharma R K，Maru S，Nagpal A K.Simplified procedure for creep and shrinkage effects in reinforced concrete frames［J］.Journal of Engineering Mechanics，2007，130（10）：1545－1550.

［10］Bazant Z P，Cusatis G，Cedolin L.Temperature effect on concrete creep modeled by microprestress－solidification theory［J］.Journal of Engineering Mechanics，2006，130（6）：671－680.

［11］赵西安.钢筋混凝土高层建筑结构设计［M］.2版.北京：中国建筑工业出版社，2002.

［12］沈蒲生，方辉.高层框架施工过程的模拟分析方法与近似方法的比较［J］.建筑结构，2006，36（2）：48－50.SHEN Pusheng，FANG Hui.Analysis method of tall frame building considering construction process effect［J］.Building Structure，2006，36（2）：48－50.

［13］北京迈达斯技术有限公司.MIDAS／Gen分析设计［M］.2011.

［14］肖汝诚.桥梁结构分析及程序系统［M］.北京：人民交通出版社，2002.

［15］Xiong D X，Zha X X.A numerical investigation on the behaviour of concrete filled steel tubular columns under initial stresses ［J］.Journal of Constructional Steel Research，2007，63（5）：599－611.

［16］张电杰，王元丰，雷扬.钢管混凝土轴心受压短柱徐变模型研究［J］.土木工程学报（Sup），2010，43：246－251.ZHANG Dianjie，WANG Yuanfeng，LEI Yang.A new creep model for concrete filled steel tube columns under axial compression［J］.China Civil Engineering Journal（Sup.），2010，43：246－251.

［17］王元丰.钢管混凝土徐变［M］.北京：科学出版社，2006.