Q420双角钢组合截面偏压构件弹塑性弯曲屈曲
2012-08-11俞登科李正良杨隆宇
俞登科,李正良,杨隆宇,余 周
(重庆大学a.土木工程学院;b.山地城镇建设与新技术教育部重点实验室 重庆,400045)
随着电力需求的不断增长,电网技术的持续进步,特高压工程、750、500kV双回路及多回路工程越来越多[1-2],输电线路铁塔向大型化发展,杆塔设计荷载也越来越大,常用热轧角钢在强度和规格上都难以满足大荷载杆塔的使用要求。高强双角钢组合截面构件施工、安装简便,是应用最多的组合截面形式[3-5]。此种构件用填板和螺栓将2个角钢组合在一起,可近似看作实腹式构件也可看作格构式构件。目前输电塔中此种构件的截面设计方法仍处于积累经验和探索阶段[6-7]。因此基于高强度双组合角钢的研究对于以后的工程建设、保障工程的运行安全,提高经济效益具有十分重要的意义。
在以往的工程设计中,因为电压等级低、负荷小,铁塔杆件很少遇到双组合角钢情况,对于目前输电塔中采用的双角钢组合截面构件,中国相关规程规范对其连接及连接型式并没有作出详细的规定,其他国家的规程规范也是如此[8-9]。笔者基于改进逆算单元长度法[10],编制相应程序,计算得到了Q420角钢规格为L160×12、L160×14、L160×16在不同长细比并考虑残余应力[11]影响情况下截面的弯矩 轴力相关曲线及给出建议的平面内稳定计算公式和相关的柱子曲线[12-15]。并引用 Kishi等[16]所提出的幂函数Mθ模型来表示偏压等端弯矩作用下杆件端部弯矩M与杆端转角θ的非线性Mθ关系。
1 试验概况
试验构件为L160×12、L160×14、L160×16的3种规格双角钢十字组合截面构件,材质为Q420高强钢。对应的填板厚度分别为12、14、16mm,填板材质为Q345。对每种角钢型号采用一字型填板连接。连接方式如图1(a),偏心加载装置示意图如图1(b),装置示意图如图1(c),实际装置图如图1(d)。
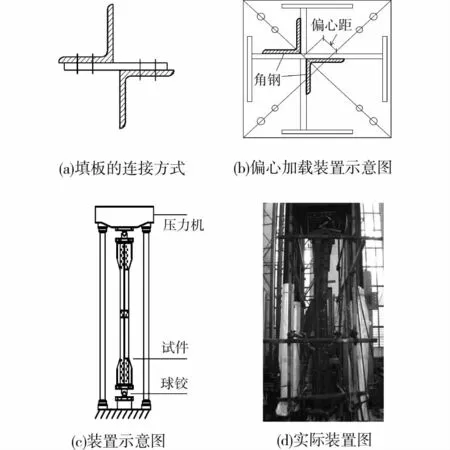
图1 填板和装置示意图
2 试验结果
整个加载过程为单调静力加载,从加载到双角钢十字组合截面偏心受压构件破坏的整个过程如下:加载初期,构件变形不明显;随着荷载的增加,构件1/2长度截面周围,在角钢肢尖边缘出现局部屈曲,并逐渐向整体屈曲过渡,此时构件并未破坏,还能继续承受荷载;随荷载进一步增加,构件发生以整体弯曲屈曲为主的破坏。加载过程中由于构件的初弯曲、荷载作用的初偏心、加工过程中引起的残余应力及材料本身的不均匀性等初始缺陷的影响,导致同一种试验方案中的个别试件与其它试件的破坏现象有一定的差别,但总体情况比较一致。不论边界条件和结构形式如何,双角钢组合截面构件都不会发生以扭转为主的破坏。一是因为构件b/t不够大,二是因为此类开口薄壁构件只要某一肢发生翘曲,整个构件马上丧失承载能力发生整体弯曲破坏,来不及发生扭转。构件实际试验中破坏形式示例如图2。

图2 构件破坏形式示例图
3 改进逆算单元长度法
对于实际双角钢组合截面偏压构件,要考虑诸多因素,例如残余应力分析,构件的几何缺陷、端部约束,不同荷载作用条件及构件的二阶效应等都会影响实际承载能力。这样解析法就会由于所作的一些假定而无法得到精确结果。这时就需要借助于数值法来求解。对于角钢之间的填板,由于其主要作用是连接2个角钢,对承载力的提高作用有限,因此在进行数值分析时不予考虑,将组合角钢截面看作实腹式构件。
3.1 基本假定
采用平截面假定和理想弹塑性假定,即弯曲前的平截面在弯曲后仍为平面,并且取用图3所示的钢材的应力 应变关系。残余应力按图4采用,其中的β根据构件的不同可取0.15~0.3,板件的两端部分为压应力,中间部分为拉应力。
3.2 轴力P 弯矩M 曲率Φ的关系
在计算ΜΡΦ关系曲线时,须将双角钢截面划分为足够多的单元并且先确定单元的应变,再根据钢材的应力 应变关系确定单元应力。计算的主要目的是建立截面的内力与变形之间的数值计算结果。将双角钢组合截面划分成有限个单元,如图5所示,单元面积为Ai,截面任一点的应变是轴力引起的应变ε0,弯曲应变Φzi和残余应变εri=σri/E的代数和,即

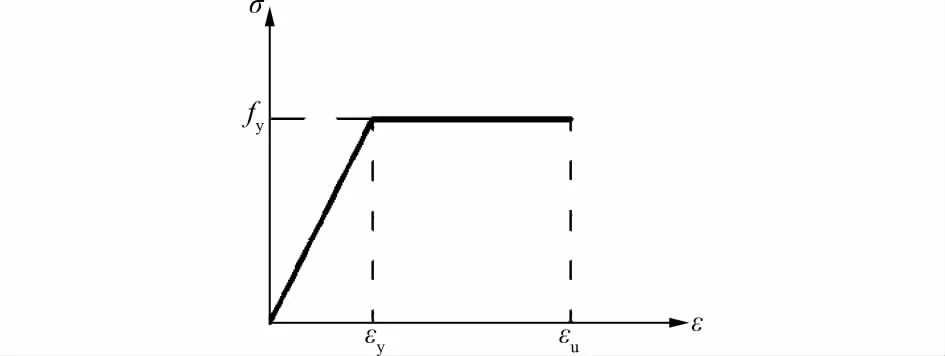
图3 钢材应力 应变关系
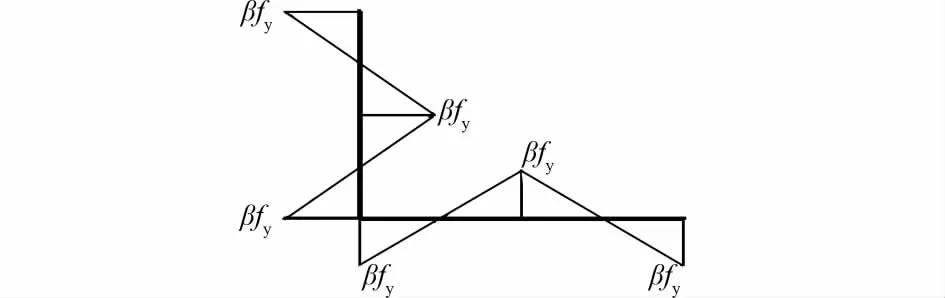
图4 单肢角钢截面残余应力分布

图5 截面单元的划分
如果截面处在弹性状态,则偏压构件和受弯构件一样,弯矩和曲率呈正比关系,与轴心压力完全无关。但是在弹塑性状态,因各截面塑性发展的程度不同,弯矩与曲率的关系还与轴心压力有关。此时,已经屈服的单元应力与应变不再呈比例关系,Μ ΡΦ关系需要通过数值积分获得,而截面划分单元的数量将会影响计算结果的精确度及工作量。以εy=σy/E表示屈服应变,任一单元面积上Ai的应力均取其平均值。
由式(1)~(4)即可求得偏压构件在弹塑性状态下的ΜΡΦ关系。具体做法是:先给定P和Φ,假定ε0=P/AE,由式(1)~(3)可求得压力F,若P与F间的差别超过了一定精度,则修正ε0进入下一轮计算,修正公式为:
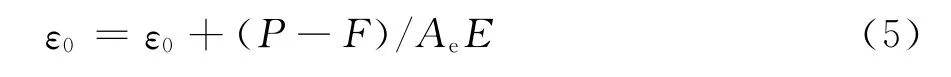
直到满足要求为止,此时即可由式(4)求得M。改变Φ值重复计算,就能得到ΜΡΦ关系曲线。
3.3 改进逆算单元长度法
将偏压杆视为若干段所组成,各段挠曲线用泰勒级数展开表示为:
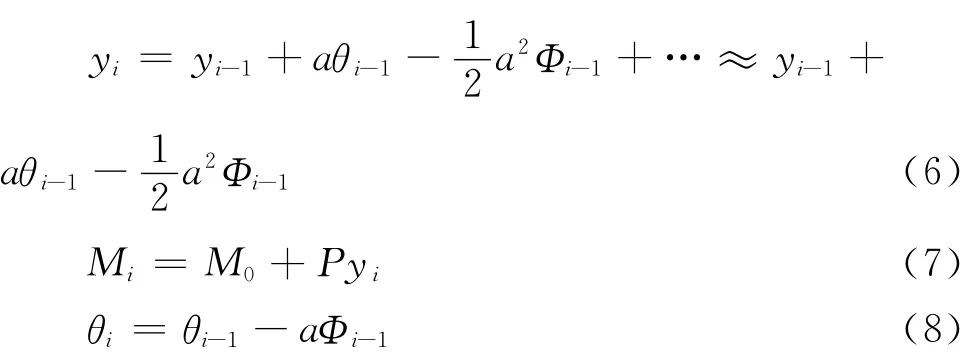
段长固定取为a=10mm。由已知杆端弯矩M0通过前面得到的ΜΡΦ关系曲线查得对应曲率Φ0。并且设杆端初始转角为θ0。按照式(6)~(8)循环计算直到θm=0为止,循环次数记为m,则此时得到杆件长度为L=2ma。在固定轴力N0和端弯矩M0不变的前提下不断改变端转角θ0可求得许多对应不同的杆长L,直至Li+1<Li,即可得到此固定N0,M0下的极限承载长度Lmax。当N0为某一定值,改变端弯矩M0值,重复上述计算步骤可得到不同端弯矩作用下的极限长度Lmax。根据求得的N0为定值下不同端弯矩作用下的Lmax,采用分段有理插值即可得到λ=25、45、65下的端弯矩。改变轴压力N0,就可求得绘制相关曲线所需要的数据,见图6,其中虚线为残余应力较大。
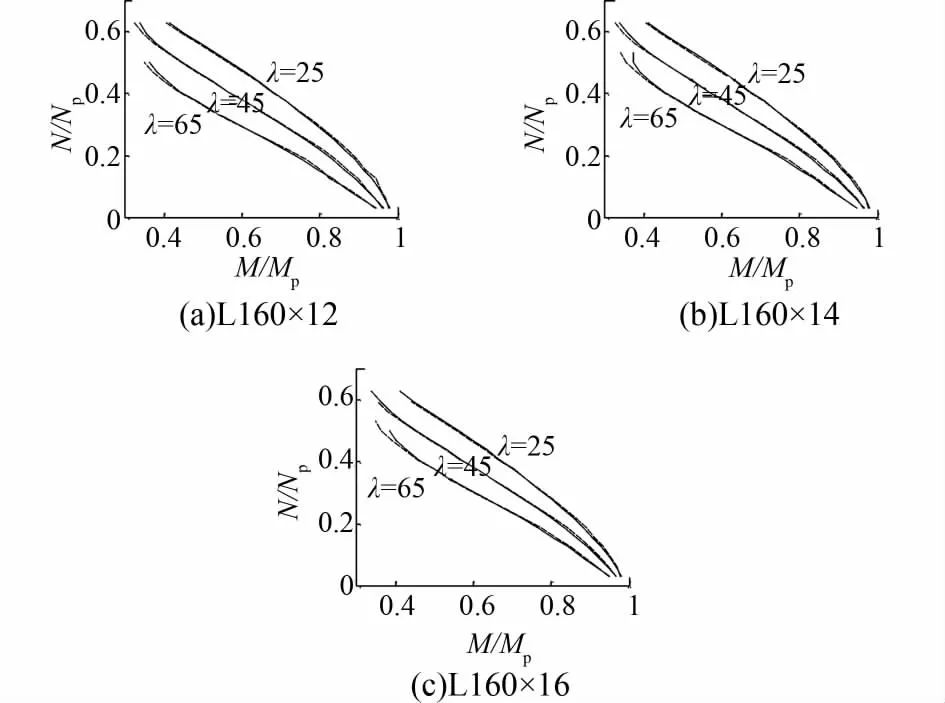
图6 相关曲线
由图6所示相关曲线可见,弯矩越大,则残余应力的不利影响愈小,对于短粗的杆,在相当范围内还起到了有力影响。绘制得到很多组λ的相关曲线后,再借用边缘屈服准则导出的相关公式的形式对上诉曲线进行拟合。建议取β为0.5,(考虑塑性部分深入),塑性部分发展系数γx取为1.02,则得到弯矩作用平面内稳定的计算式:
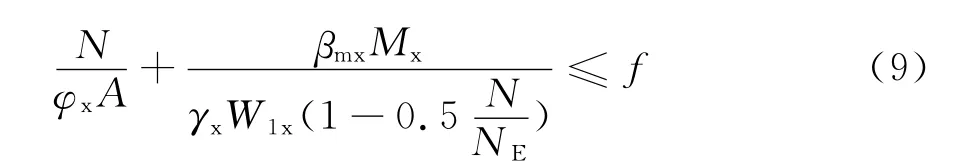
拟合情况见图7,虚线为(9)式计算拟合值。
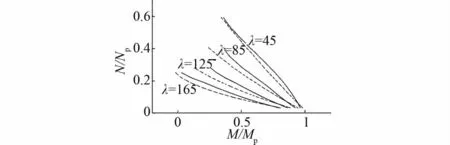
图7 偏心压杆的相关曲线
对其他2种角钢规格也进行了相应拟合,拟合效果较好,因此建议公式以上述式(9)计算此类构件平面内稳定,并可作为设计参考。由建议公式可以得到对应不同λ下的φx值,进而就可绘制得到Q420钢材截面形式为组合双角钢情况下临界应力φx与长细比λ之间的关系曲线,即柱子曲线,见图8。
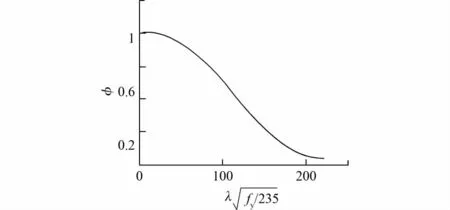
图8 柱子曲线
因在固定轴力N0和端弯矩M0不变的前提下不断改变端转角θ0可求得许多对应不同的杆长L,直至Li+1<Li,可得到此固定N0、M0下的极限承载长度Lmax。由此也可以得到固定轴力N0和端弯矩M0下端转角θ0与杆长L的关系曲线。当N0为某一定值,不断改变端弯矩M0值,就可以得到很多组端转角θ0与杆长L的关系曲线。对于同一个杆长L下,亦可得出多组不同端弯矩M0和对应的端转角θ0,由此即可得到端弯矩M0和端转角θ0的关系曲线,见图9。由图可见,残余应力对Mθ关系只是略有影响,但是不大。
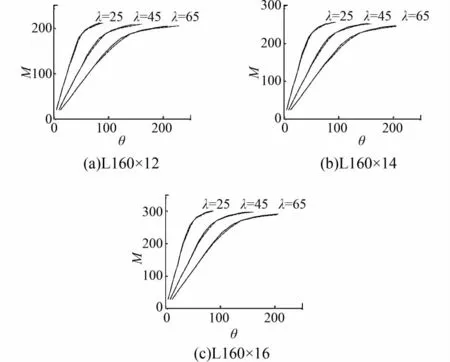
图9 M θ关系曲线
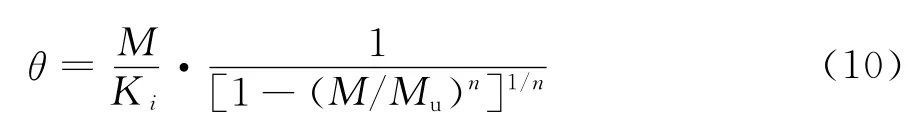
式中:Ki为弹性初始刚度,Mu为极限弯矩承载力,是Mθ关系曲线的限制值,n为Mθ关系曲线的形状系数,用于调整曲线的曲率。此处建议取为5,以L160×14为例,拟合情况见图10,虚线为按式(9)的拟合值。
分别绘制得到长细比λ=45、85、125、165情况下的Mθ关系曲线。并以Kishi和Chen所采用的幂函数模型来进行拟合。其形式为:
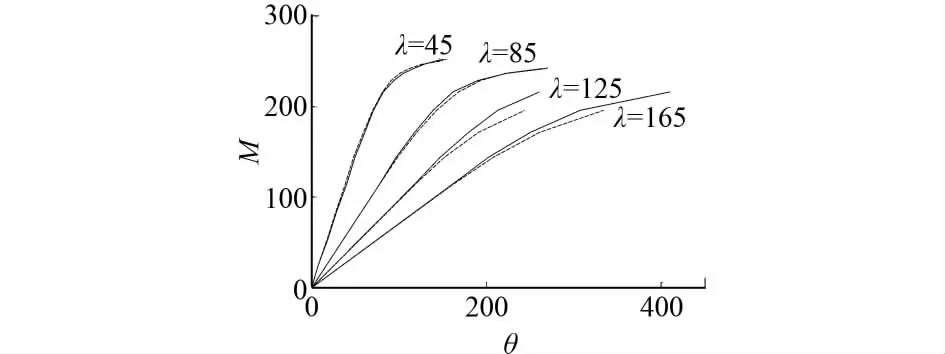
图10 M θ关系曲线及拟合值
由图10可见,拟合情况比较理想。因此,建议采用Kishi和Chen所提出的幂函数模型作为3种规格双角钢杆件端部弯矩M与杆端转角θ的非线性Mθ关系的设计参考。
4 结 论
通过以上分析可以得到如下结论:
1)双角钢十字组合截面偏心受压构件破坏模式以整体平面内弯曲屈曲破坏为主。
2)采用改进逆算单元长度法得出平面内稳定的建议计算式(9),取β为0.5,塑性部分发展系数γx为1.02。
3)对于所研究规格的双角钢偏压构件杆件端部弯矩M与杆端转角θ的非线性Mθ关系建议采用Kishi和Chen所提出的幂函数模型作为设计参考。
[1]秦永坚,王登科,唐其练,等.500kV双回路输电线路铁塔采用Q420高强钢的研究[J].电力勘测设计,2007(3):60-65.QIN Yongjian,WANG Dengke,TANG Qilian,et al.Application of high-strength steel Q420in 500kV double-circuit transmission line iron tower[J].Electric Power Survey & Design,2007(3):60-65.
[2]韩钰,徐德录,杨建平,等.Q420高强钢在特高压输电工程中的应用研究[J].电力建设,2009,30(4),33-35.HAN Yu,XU Delu,YANG Jianping,et al.Research on applications of Q420high-strength steel in UHV transmission projects[J].Electric Power Construction,2009,30(4):33-35.
[3]Pocock G.High strength steel use in Australia,Japan and the US [J].The Structural Engineer,2006,84(21):27-30.
[4]杨靖波,李茂华,杨风利,等.我国输电线路杆塔结构研究新进展[J].电网技术,2008,32(22):78-83.YANG Jingbo,LI Maohua,YANG Fengli,et al.New advances in the study of transmission tower structure of China[J].Power System Technology,2008,32(22):78-83.
[5]Kitipornchai S,Albermani F G,Kang W,et al.Some practical aspects of modeling lattice towers[C]//The Fourth International Conference on Advances in Steel Structures,Shanghai,2005:369-376.
[6]李振宝,石鹿言,刑海军,等.Q420双角钢十字组合截面压杆承载力试验[J].电力建设,2009,30(9):8-11.LI Zhenbao,SHI Luyan,XING Haijun,et al.Research on bearing capability of Q420double-angle steel cross combined section[J].Electric Power Construction,2009,30(9):8-11.
[7]李振宝,杨小强,韩军科,等.双角钢十字组合截面偏心受压构件承载力实验研究[J].工程建设与设计,2009(11):21-24.LI Zhenbao,YANG Xiaoqiang,HAN Junke,et al.Research on bearing capacity of eccentric compression members with combined angle iron cross-section [J].Architectural and Structural Design,2009(11):21-24.
[8]IABSE.Use and application of high performance steels for steel structures[M].Zurich:IABSE,2005.
[9]AISC.Specification for structural steel buildings[M].Chicago:AISC,2005.
[10]李开禧,须宛明.关于“逆算单元长度法”的改进[J].重庆建筑工程学院学报,1989,11(3):37-42.LI Kaixi,XU Wanming.An improvement on ‘The inverse calculation segment length method’[J].Journal of Chongqing Institute of Architecture and Engineering,1989,11(3):37-42.
[11]班慧勇,施刚,邢海军,等.Q420等边角钢轴压杆稳定性能研究-残余应力的试验研究[J].土木工程学报,2010,43(7):14-21.BAN Huiyong,SHI Gang,XING Haijun,et al.Stability of Q420high strength steel equal-legangle members under axial compression-experimental study on the residual stress [J].China Civil Engineering Journal,2010,43(7):14-21.
[12]Chen W F,Atsuta T.Theory of beam-columns,Vol.1[M].New York:McGrow-Hiu,Inc,1976.
[13]Liu Y,Hui L B.Finite element study of steel single angle beam-columns [J].Engineering Structures,2010,32,2087-2095.
[14]Hui L B.Beam-column behaviour of steel single angles[D].Halifax:Dalhousie University,2007.
[15]陈骥.钢结构稳定理论与设计[M].3版.北京:科学出版社,2006:74-123.
[16]Kishi N,Chen W F.Moment-rotation relations of semirigid connections with angles[J].Journal of Structural Engineering,ASCE,1990,116(7):1813-1834.
