泥水盾构隧道施工引起的地面沉降分析及预测
2012-08-11林存刚吴世明张忠苗李宗良刘冠水
林存刚,吴世明,张忠苗,李宗良,刘冠水
(1.浙江大学a.软弱土与环境土工教育部重点实验室;b.岩土工程研究所,杭州310058;2.杭州庆春路过江隧道有限公司,杭州310002)
近年来,泥水盾构越来越广泛地应用于城市水底隧道施工,如上海上中路隧道、上海长江隧道、武汉长江隧道、南京长江隧道、杭州庆春路过江隧道、杭州运河隧道、海宁钱江隧道等[1-2]。对于盾构施工引起的地面沉降,许多学者进行了研究,研究方法主要为经验公式法、解析法和数值模拟法[3-6],然而这些研究大都针对土压平衡盾构,而对于泥水盾构的研究相对较少。泥水盾构与土压平衡盾构相比,泥水压力传递快速而均匀,开挖面平衡土压力的控制精度更高,地面沉降量的控制精度更高[7]。而泥水盾构用于水底隧道施工,穿越堤防和水底浅覆土区域,对地面沉降的控制要求更为严格。在上海若干水底隧道工程施工中,曾发生了大堤防汛墙底板渗水、防汛闸门变形、防汛墙倒塌等威胁提防安全的事故[8]。因此,深入研究泥水盾构施工引起的地面沉降,具有十分重要的意义。
结合杭州庆春路过江隧道泥水盾构施工地面沉降实测数据,分析了泥水盾构施工引起的地面沉降的特征及规律,总结了影响地面沉降的因素,并给出了地面沉降的预测公式。
1 工程概况及地质条件
1.1 工程概况
杭州庆春路过江隧道南北方向垂直穿越钱塘江,盾构段总长3 532.442m,其中东线长1 765.478m,西线长1 766.924m。管片外径11.3m,内径10.3m,厚50cm,环宽2m。管片采用通用契型环,采用6标准块+2邻接块+1封顶块的分块形式,错缝拼装,纵环向采用高强螺栓连接。
盾构隧道采用两台泥水平衡盾构机从江南盾构工作井开始掘进,始发段纵向坡度为-4.25%。盾构主机长11.4m,后配3节拖车,上载砂浆泵、电器液压设备、主控室等,长约20m。盾构主机总重1 100t,外径11.65m。
1.2 工程及水文地质条件
盾构施工主要穿越③层粉砂夹粉土、④层淤泥质粉质粘土、⑤层粉质粘土、⑥层粉质粘土、⑦层粉细砂和⑧层圆砾。各土层物理力学指标见表1。隧道穿越土层剖面见图1。
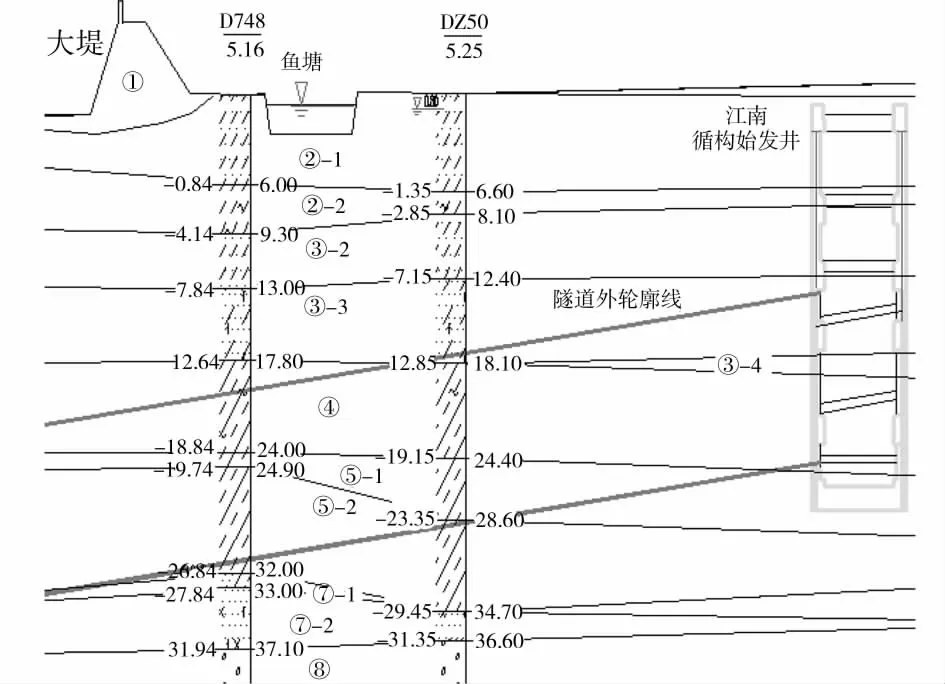
图1 隧道穿越土层剖面图
孔隙潜水赋存于场区浅部人工填土及其下部粉、砂性土层内,水位高,渗透性好。⑦层砂土、⑧层圆砾为承压水层,承压水位高,透水性强。
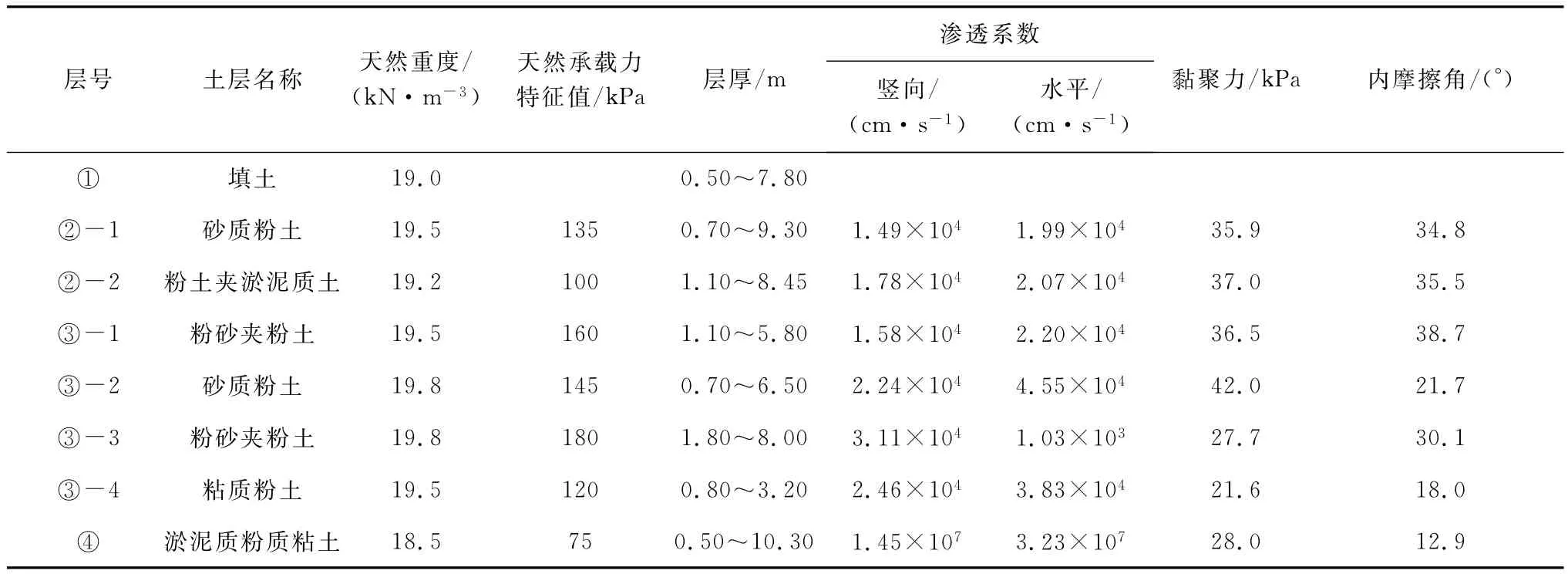
表1 场地主要土层物理力学指标
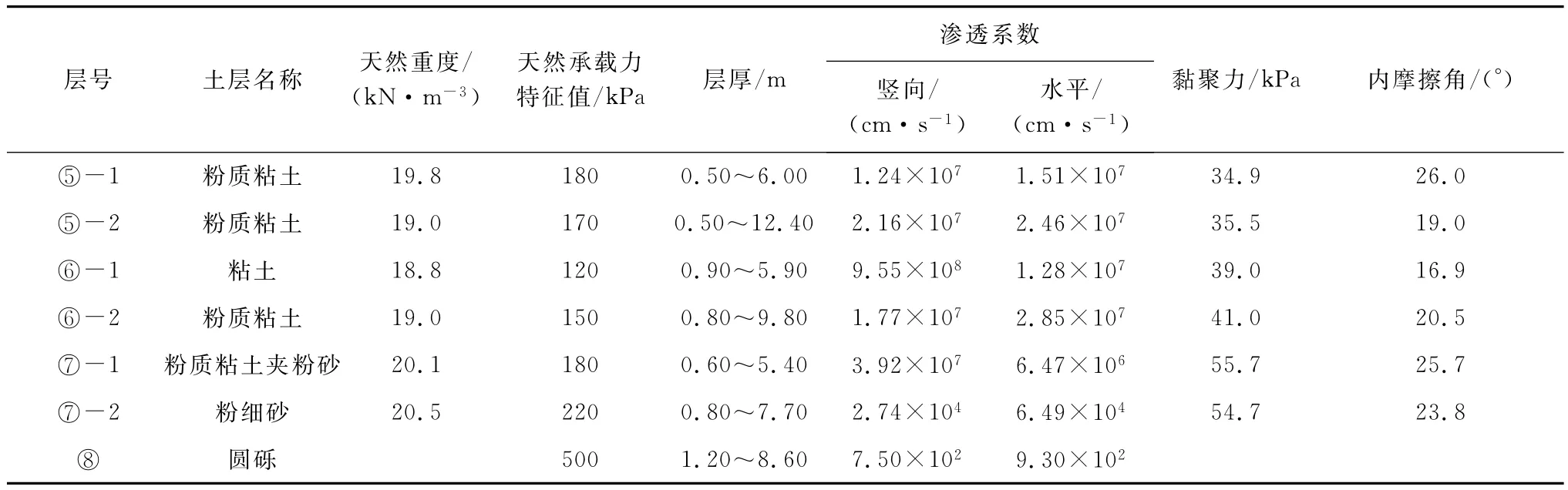
续表1
2 地面沉降监测布置
地面沉降监测从江南工作井至钱塘江南岸大堤一共布置19个断面,编号D1~D18、XB。其中西线隧道监测断面标记为WD,东线为ED,XB仅布置于西线。监测断面布置情况如图2所示。其中D1~D6因处于加固区,数据失真,数据未采用;D7~D12、D17、D18、XB所处地面隧道施工前为农田;D13~D16位于钱塘江南岸大堤之上。笔者仅对西线盾构施工引起的地面沉降进行分析,即 WD7~WD12、WD17、WD18、XB断面。

图2 地表监测断面平面布置示意图
3 地面沉降监测及分析
3.1 西线隧道横断面地面沉降
对于隧道施工引起的横向地面沉降的估算,工程实践中应用最为广泛的为Peck公式[3、9]:
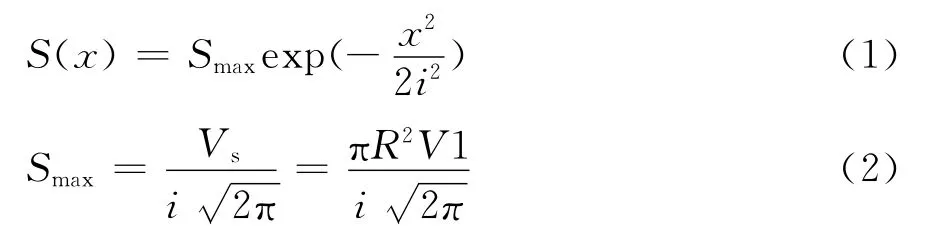
式中:S(x)为地层损失引起的地面沉降;x为距隧道轴线的距离;Smax为隧道轴线处地层损失引起的地面沉降;i为地表沉降槽宽度系数;Vs为隧道单位长度地层损失;η为地层损失率,为地表沉降槽的面积与隧道开挖面积之比;R为隧道开挖半径。
使用Peck公式预测横向地面沉降时,最为关键的是确定地层损失率V1以及沉降槽宽度系数i的取值。其中地层损失率V1取值受土质、隧道工法及施工参数控制等影响,具有很大的离散性和地区及施工经验性[10-11]。对于沉降槽宽度系数i的取值,国内外许多学者进行了实测及试验研究[12-15],其中应用最为广泛的是O’Reilly&New(1982)[15]根据伦敦地区经验提出的:

式中K为沉降槽宽度参数,定义为横断面地面沉降曲线拐点至隧道轴线水平距离与隧道轴线埋深之比;z0为隧道轴线埋深。
对 WD7~WD12、XB、WD17、WD18,9个监测断面横向地面沉降进行分析。
分析表明:西线隧道各监测断面横向地面沉降特征及规律基本一致,均可用Peck公式较好地拟合。
图3、4、5分别为 WD8、WD12、WD17断面横向地面沉降,图中地面隆起记为正值。图中沉降曲线标记,如图3中第1条沉降曲线标记“0d,11.329m”表示盾构盾尾离开WD8断面0d,盾构切口离开WD8断面11.329m。
图3~5可见:
1)盾构切口到达监测断面之前,地面随切口泥水压力的设定,时有隆起,时有沉降。
2)在盾构盾尾离开监测断面之前,地面沉降较小,且沉降曲线较无规则。
3)盾尾离开监测断面时,沉降量和沉降速度陡增,此后横向地面沉降曲线开始呈现隧道轴线位置沉降最大,向两侧递减的规律。
4)盾尾脱离监测断面初期,由于同步注浆作用,隧道轴线两侧或一侧约10m之外地面出现隆起。
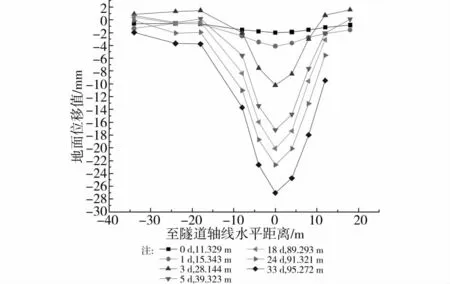
图3 WD8断面地面沉降
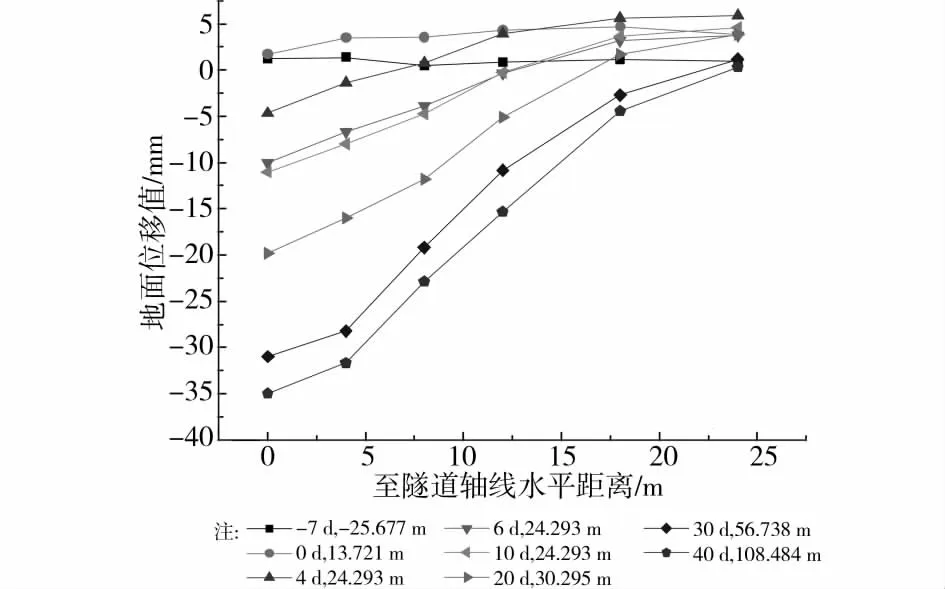
图4 WD12断面地面沉降
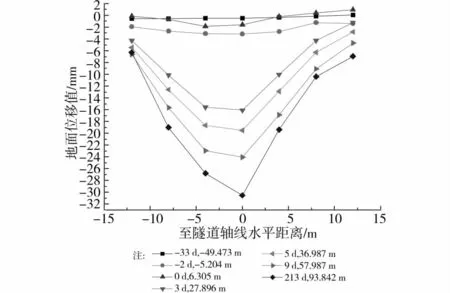
图5 WD17断面地面沉降
Peck公式假定隧道施工引起的地面沉降是在不排水情况下发生的,沉降槽的体积等于地层损失的体积[9]。分析发现,西线隧道地面沉降,在盾构脱离监测断面0~5d或6d之内,沉降速度和沉降量最大,而之后沉降速度出现转折,开始明显变慢。一般认为,在盾尾脱离监测断面之后,由于建筑空隙的产生,会引起比较大的地层损失沉降;之后的沉降主要由扰动土体固结引起;地层损失沉降的速度大于固结沉降速度。故认为盾尾脱离5d或6d之前的地面沉降主要由地层损失引起,选取该天的地面沉降值用Peck公式加以拟合。
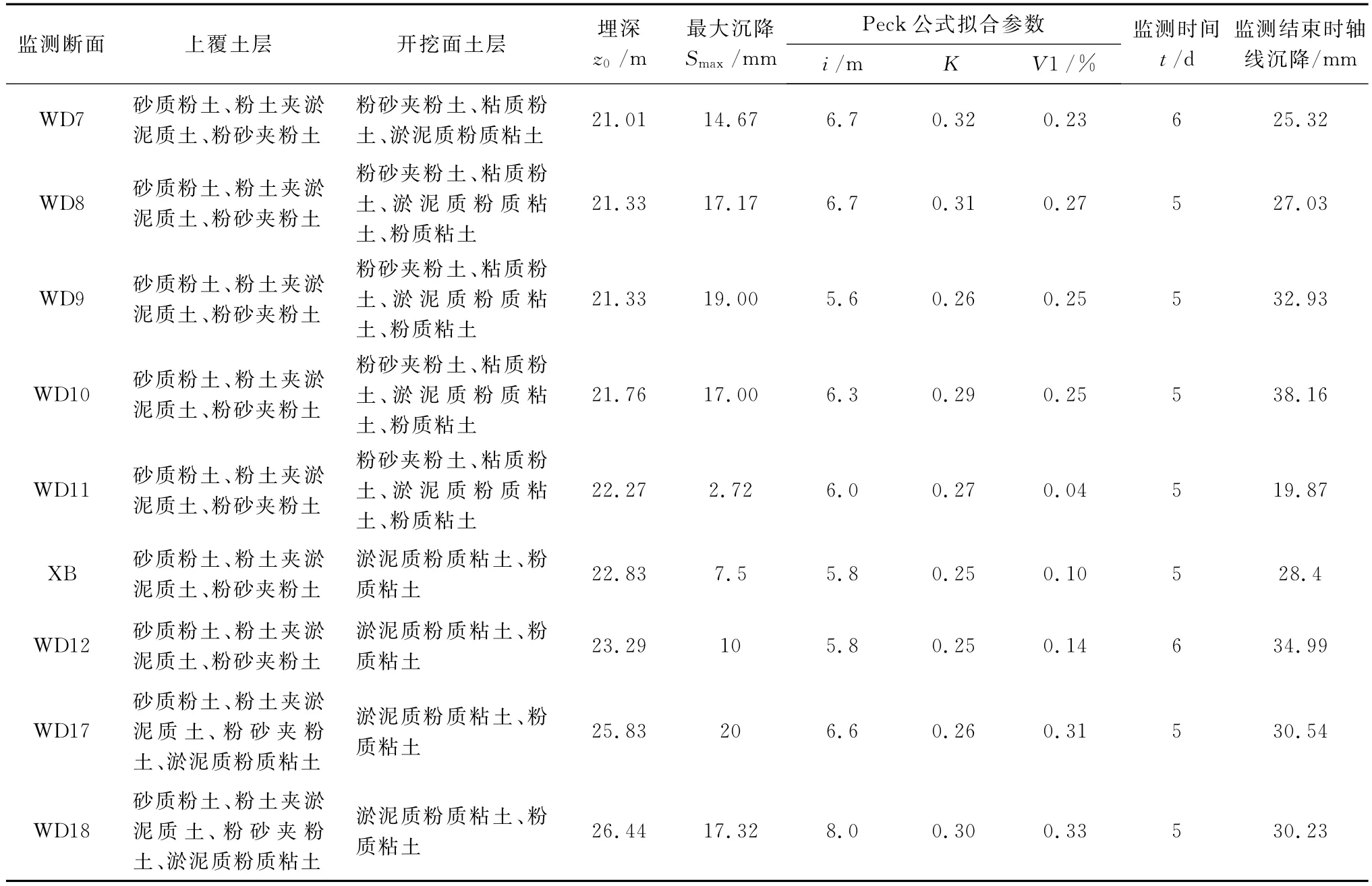
表2 西线隧道Peck公式拟合结果
图6~8分别为 WD8、WD12、WD17,盾尾脱离监测断面5d或6d时,横断面地面沉降用Peck公示拟合的情况。t为盾尾离开监测断面的时间。各断面地面沉降Peck公示拟合结果统计于表2。
图6~8可见,所选取的3个断面,WD17断面地面沉降Peck公示拟合最好,其次为WD8,最差为WD12。结合图3~5,WD12在切口到达前以及盾尾离开初期地面产生较大隆起;WD8在盾尾脱离时轴线一侧约10m外产生较小隆起;而WD17断面只在盾构通过期间,地面出现微量隆起。
盾构切口靠近监测断面时,泥水压力设定大于开挖面初始水土压力时,在附加应力作用下,开挖面上前方土体上抬,进而引起地面隆起;盾尾脱离监测断面初期,同步注浆压力较大时,同样会引起地面上抬。各监测断面地面沉降Peck公式拟合时发现,当切口压力及同步注浆压力作用下地面出现较大隆起时,拟合情况较之于地面隆起小或者无隆起的断面要差。地层损失沉降比较有规则,一般呈现正态分布曲线形式;而由于切口泥水压力及同步注浆压力引起的地面隆起较无规则,会使总沉降曲线偏离高斯曲线分布。
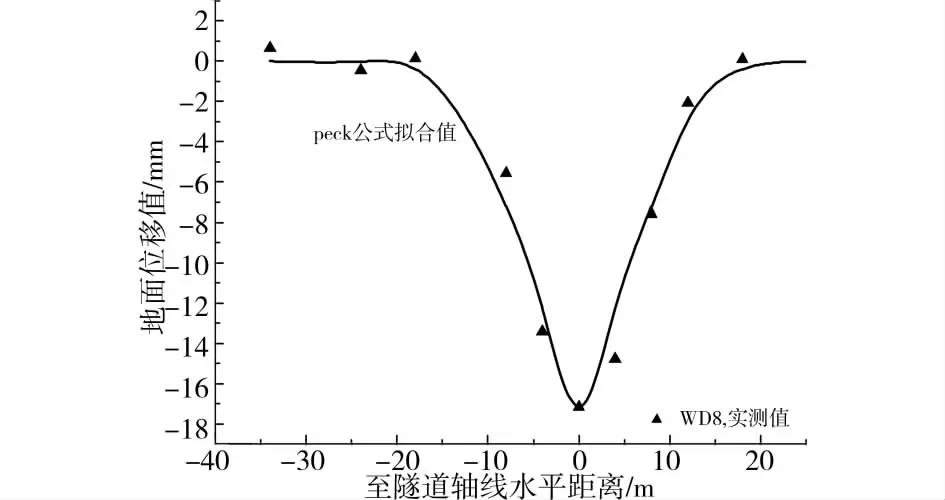
图6 t=5d时WD8断面实测沉降曲线及Peck公式拟合曲线
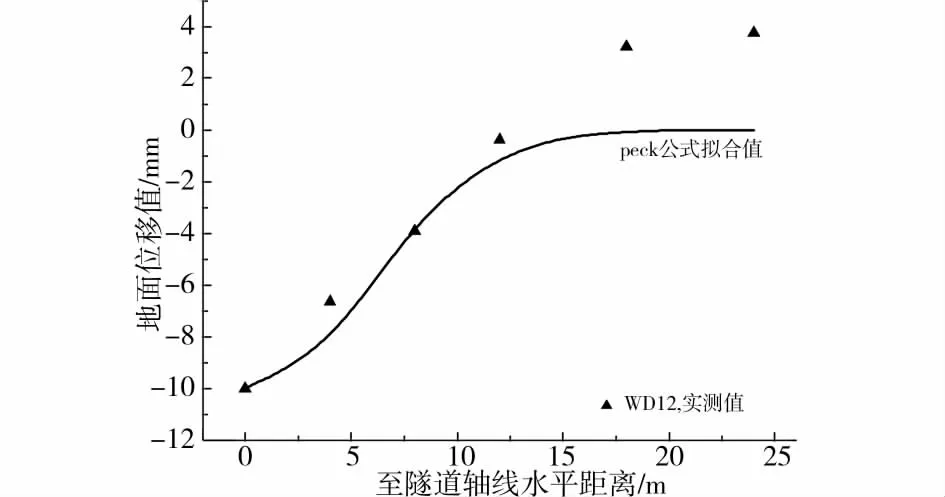
图7 t=6d时WD12断面实测沉降曲线及Peck公式拟合曲线
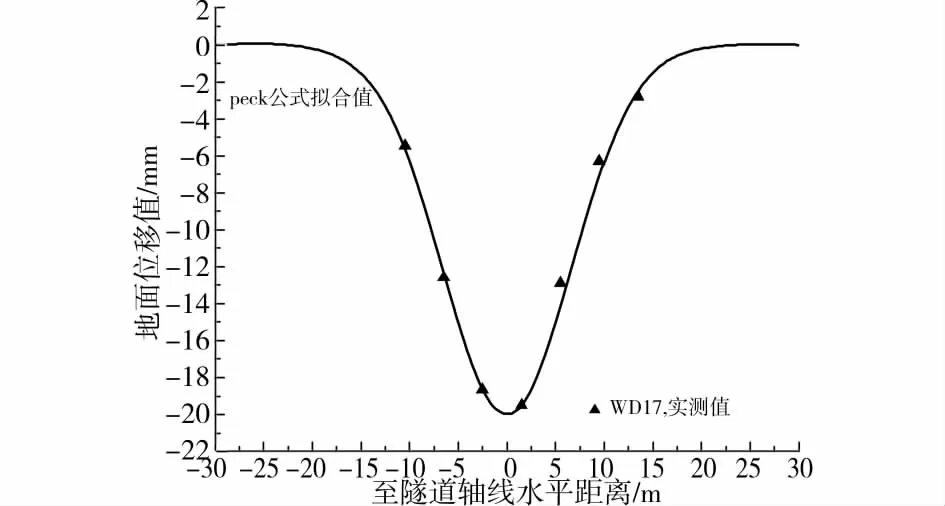
图8 t=5d时WD17断面实测沉降曲线及Peck公式拟合曲线
图7可见,适当提高切口泥水压力及同步注浆压力使地面出现微量隆起,可以抵消部分地层损失,降低地面总沉降量,并减少地面沉降范围。但切口泥水和同步注浆压力也不能设置过大,以避免较大的地面隆起危及地表及地下建(构)筑物的正常使用和安全。
表2可见,西线隧道各个监测断面地面沉降槽宽度参数K取值比较集中,在0.25~0.32之间;而地层损失率V1的取值受施工参数控制影响离散性较大,取值在0.04%~0.33%之间。
3.2 西线隧道纵向地面沉降
对于隧道施工引起轴线上方地面沉降随时间变化的预测,很多学者进行了研究[16-19]。Fang等[16]通过对Taipei MRT CH18B1隧道沉降观测分析,提出采用双曲线模型估算隧道轴线上方地面沉降随时间的变化:

式中,S(t)为t时刻隧道轴线上方地面最大沉降量;t为盾尾离开监测断面的时间(以盾尾离开监测断面前1天算起);a、b为双曲线常数。
魏纲等[16]通过对11个隧道工程实例分析发现,上述双曲线模型用于预测隧道工后沉降时,精度较高。刘松樵[19]采用双曲线模型对上海地铁一号线及延安东路隧道盾构盾尾离开后地面沉降曲线进行拟合,效果较好。
然而双曲线模型仅用于隧道施工引起的地面固结沉降的预测,忽略了盾构切口靠近时以及盾构通过期间产生的地层损失沉降。
笔者在Fang提出的传统双曲线模型的基础上,添加参数c,以考虑盾构切口靠近时以及盾构通过期间产生的地面位移,用修正后的双曲线模型拟合该工程隧道轴线上方地面沉降随时间变化曲线。修正后的双曲线模型为:

式中:S(t)为t时刻隧道轴线上方地面最大沉降量,沉降记为负值,mm;t为盾尾离开监测断面的时间,d;t=0时,盾尾到达监测断面;a为双曲线常数,表征盾尾脱离初期(t≤10d)地面沉降速度,a越大,盾尾脱离初期沉降速度越小;b为双曲线常数,决定地面最终沉降量大小,b越小,最终沉降量越大;c为双曲线常数,盾构切口到达前以及盾构通过期间产生的地面位移。
图9~10分别为WD7、WD10实测轴线地面沉降随时间变化曲线用修正双曲线模型拟合的情况。
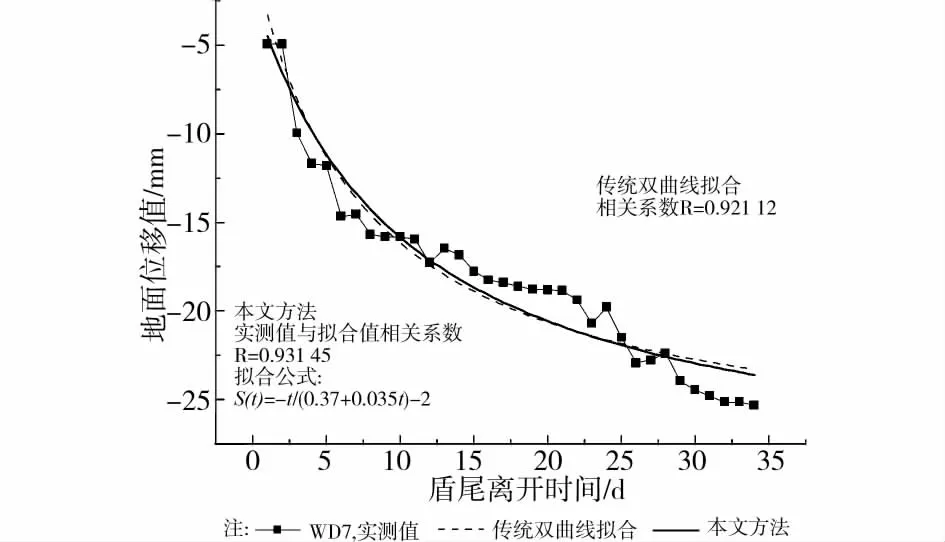
图9 WD7轴线地面沉降随盾尾离开时间变化实测及拟合值
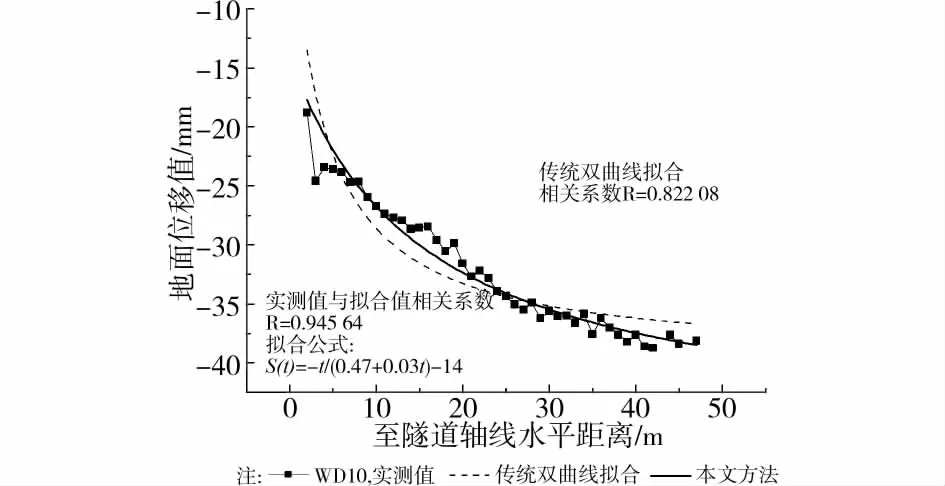
图10 WD10轴线地面沉降随盾尾离开时间变化实测及拟合值
使用修正后的双曲线模型,对各监测断面轴线地面沉降随时间的变化曲线均可以较好地拟合,且预测精度高于传统的双曲线模型。拟合结果统计见表3。
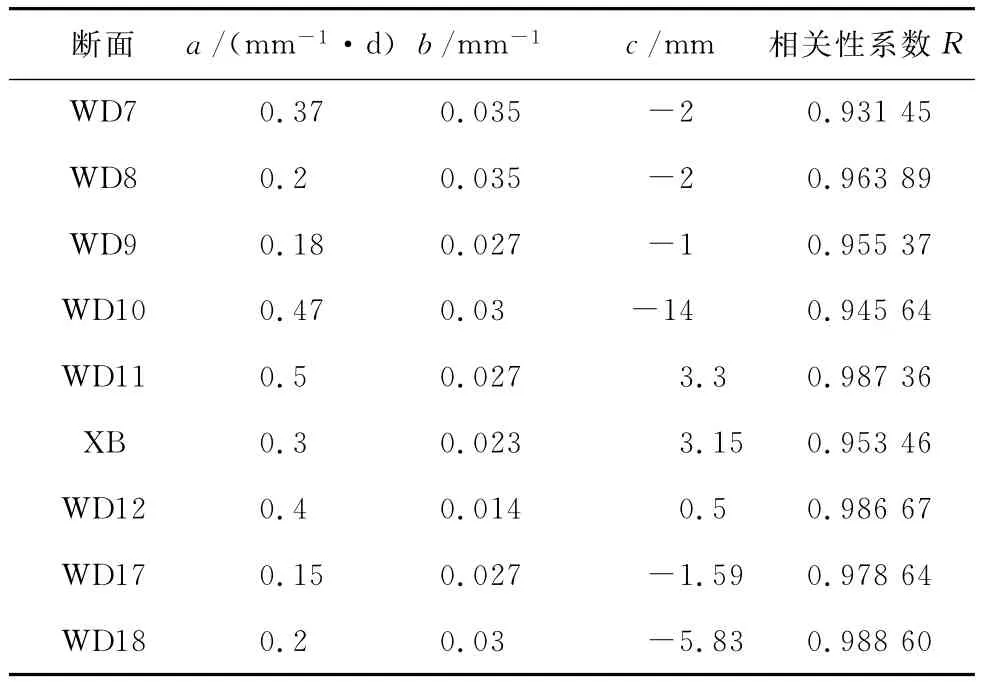
表3 西线隧道轴线地面沉降双曲线模型拟合结果
各监测断面拟合公式,a取值范围0.15~0.5mm-1·d,b取值0.014~0.035mm-1,c取值-14~3.3mm。
3.3 西线隧道盾构通过各个阶段地面沉降
盾构隧道施工引起的地面位移,根据盾构与监测断面的相对位置以及形成机理,可分为4个阶段:
1)切口到达前地面位移:当切口压力设置小于开挖面初始水土压力时,开挖面应力松弛,引起切口上前方地面沉降;当切口压力设置大于开挖面初始水土压力时,附加应力作用下会引起切口上前方地面隆起。合理的切口泥水压力设置是控制该阶段地面位移的关键。
2)盾构通过时地面位移:良好的盾构掘进姿态,以减少盾构机的俯仰、偏转以及横向偏移,减少超挖和减轻盾构与周围地层的摩擦、挤压,可降低该阶段地面沉降。
3)盾尾沉降:盾尾脱离监测断面时,由于建筑空隙的产生,会引起较大的地层损失沉降。同步注浆及时充分地填充建筑空隙,可有效地降低盾尾沉降。本文取盾尾离开监测断面0~5d或6d内的沉降为盾尾沉降。
4)固结沉降:主要为盾构施工扰动土体固结沉降,除受到土层影响之外,施工扰动的大小也是其重要的影响因素。本文取盾尾脱离5d或6d后的沉降为固结沉降。
以上4个阶段沉降值分别记为S1、S2、S3、S4,对应沉降速度记为V1、V2、V3、V4,地面总沉降量S=S1+S2+S3+S4,监测周期内总沉降速度记为V。各监测断面各阶段轴线地面沉降值及占总沉降的比例统计于表4。
表4可见:
1)S1取值范围-3.41~3.16mm,V1取值范围-1.14~0.10mm/d,占总沉降的比例-12.01%~10.35%。该阶段沉降主要受到切口泥水压力设定的影响,由于各断面切口泥水压力设定的不同而表现出较大波动。
2)S2取值范围-1.87~5.66mm,V2取值范围-0.79~2.83mm/d,占总沉降的比例-9.41%~18.72%。
3)WD11断面同步注浆作用下地面出现较大隆起,WD12断面受到盾构长时间停机的影响,使得该两个断面地面沉降规律与其他断面差别较大。在分析S3及S4取值时该两个断面不予考虑。S3取值范围11.49~23.58mm,V3取值范围2.18~5.90 mm/d,占总沉降的比例38.01%~64%,平均为57.27%。该阶段沉降主要受到盾尾同步注浆影响。
4)S4取值范围9.86~14.58mm,V4取值范围0.31~0.86mm/d,占总沉降的比例36%~50.67%,平均为41.08%。
以上分析可见,对于该工程泥水盾构施工引起的地面沉降,盾尾脱离初期(0~5/6d)盾尾沉降量和沉降速度最大,约为总沉降量的57.27%;盾构切口到达前以及盾构通过时的地面沉降,受切口压力设定以及盾构姿态控制波动较大,位移值控制在±5 mm之内;后期固结沉降占总沉降的比例较大,约为41.08%。由于各断面监测时间有限,固结沉降在监测结束时仍继续进行,因此,其所占比例还会加大。由此可见,该工程泥水盾构施工引起的地面沉降,大部分为盾尾沉降及扰动土体长期固结沉降,而盾构穿越之前的位移相对较小,甚至起到抵消后续沉降的作用。
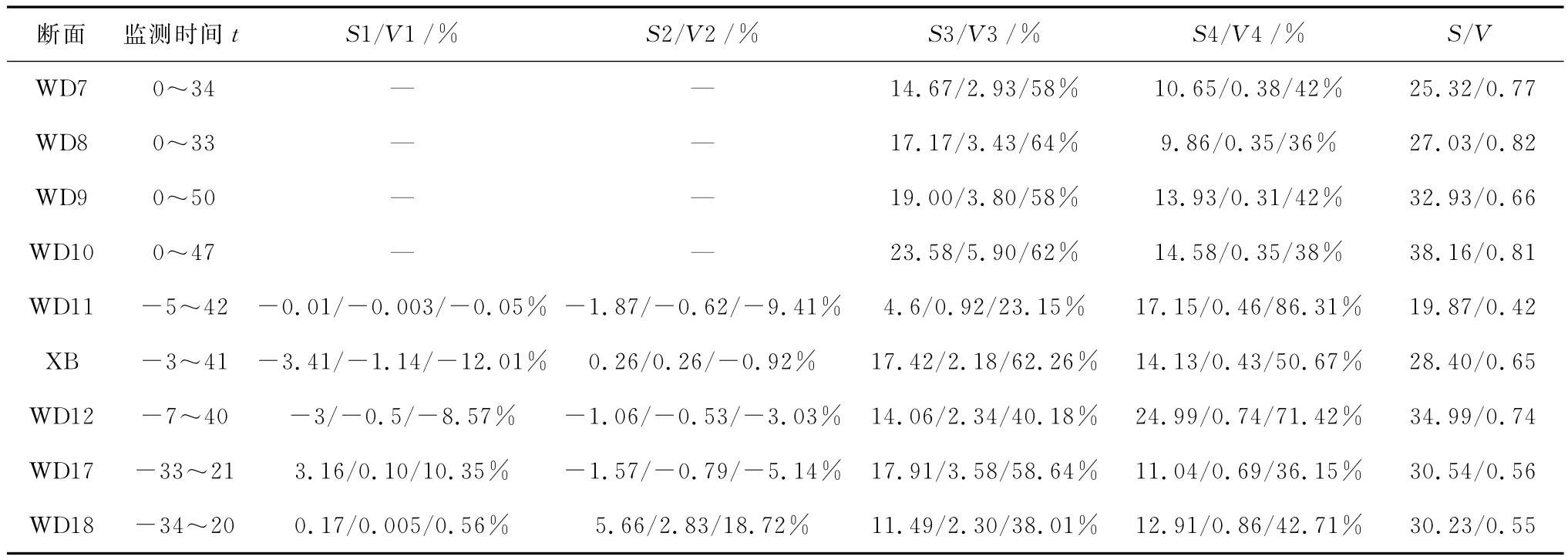
表4 西线隧道盾构穿越不同阶段轴线地面沉降
4 结论
1)西线隧道盾构施工引起的地面沉降可用Peck公式较好地拟合,各监测断面地面沉降槽宽度参数K取值比较集中,在0.25~0.32之间;而地层损失率V1的取值受施工参数控制影响离散性较大,取值在0.04%~0.33%之间。
2)泥水盾构在软土地层中施工,大部分地面沉降为盾构脱离0~5d或6d内的盾尾沉降以及扰动土体长期固结沉降,分别约占总沉降量的57.27%和41.08%;盾尾脱离监测断面0~5d或6d期间,地面沉降速度最大。
3)适当提高切口泥水压力以及同步注浆压力使地面出现微量隆起,可以抵消部分地层损失,降低地层损失率及地面沉降范围,有利于沉降控制。
4)地层损失沉降比较有规则,符合高斯曲线分布形式;而由于切口泥水压力及同步注浆作用引起的地面隆起较无规则,会使总沉降曲线偏离正态分布曲线。
5)引入新的参数c,以考虑盾构切口靠近时以及盾构通过期间产生的地面沉降的修正双曲线模型,可以较精确地拟合轴线地面沉降随盾尾离开时间的变化曲线,可用于泥水盾构软土地区施工引起的长期地面沉降的预测。
[1]杨红禹,周建民.论我国越江隧道的发展[J].地下空间,20(3):209-213.YANG Hongyu,ZHOU Jianmin.On the development of under-river tunnel in China[J].Underground space,20(3):209-213.
[2]孙钧.桥梁/隧道跨越江河湖海的方案比选与分析[C]//上海:第四届中国隧道国际峰会,2010.
[3]Gonzalea C,Sagaseta C.Patterns of soil deformations around tunnels.Application to the extension of Madrid Metro[J].Computers and geotechnics,2001,28:445-468.
[4]Mair R J.Tunnelling and geotechnics:new horizons[J].Geotechnique,2008,58(9):695-736.
[5]Eric L,Barry N.Settlements induced by tunneling in soft ground [J].Tunnelling and Underground Space Technology,2007,22:119-149.
[6]Tadashi H,Junichi N,Takahiro K.Prediction of ground deformation due to shield excavation in clayey soils[J].Soils and foundations,1999,39(3):53-61.
[7]周文波.盾构法隧道施工技术及应用[M].北京:中国建筑工业出版社,2004:1-22.
[8]夏懿,于瑞东,王新旗,等.越江隧道工程穿越防汛墙对防汛墙安全影响及对策探讨[J].上海水务,2008,24(4):40-45.XIA Yi,YU Ruidong,WANG Xinqi,et al.Study on safety impact and countermeasures of shield tunneling under floor wall in cross-river tunnel project [J].Shanghai Water,2008,24(4):40-45.
[9]Peck R B.Deep excavations and tunneling in soft ground[C]//State of the Art Report.Proceedings of 7thInternational Conference on Soil Mechanics and Foundation Engineering.Mexico City:[s.n.],1969:225-290.
[10]Burland J B,Standing J R,Jardine F M.Assessing the risk of building due to tunneling-lessons from the Jubilee Line Extension,London [C]//Geotechnical Engineering meeting society needs.Proc.of the Fourth Southeast Asian Geotechnical Conf.Hong Kong:K.K.S.Ho and K.S.Li.,2001,:17-44.
[11]韩煊,李宁,J.R.Standing.Peck公式在我国隧道施工地面变形预测中的适用性分析[J].岩土力学,2007,28(1):23-35.HAN Xuan,LI Ning,Standing J R.An adaptability study of Gaussian equation applied to predicting ground settlements induced by tunneling in China[J].Rock and Soil Mechanics,2007,28(1):23-35.
[12]Forth R A,Thorley C B B.Ground and building settlement due to tunneling in Hong Kong Land Subsidence[C]//Proceedings of the Fifth International Symposium on Land Subsidence,The Hague,October 1995.LAHS Publ.no.234,1995:149-160.
[13]Selby A R.Tunnelling in soils-ground movements,and damage to buildings in Workington,UK[J].Geotechnical and Geological Engineering,1999,17:351-371.
[14]Tadashi S,Toshituki H,Toshi N,et al.Observation of ground movements guring tunnel construction by slurry shield method at the Docklands light railway Lewisham extension-east London[J].Soils and foundations,1999,39(3):99-112.
[15]O'Reilly M P,New B M.Settlements above tunnels in the United Kingdom-their magnitude and prediction[C]//Proc.Tunnelling 82,Institution of Mining and Metallurgy,London:173-182.
[16]Fang Y S,Lin S J,Lin J S.Time and settlement in EPB shield tunneling [J].Tunnels and Tunnelling,1993,25(11):27-28.
[17]魏纲,张金菊,魏新江.数学模型在盾构地面长期沉降预测中的应用[J].地下空间与工程学报,2009,5(3):541-545.WEI Gang,ZHANG Jinju,WEI Xinjiang.Application of mathematic models in prediction of long-term surface settlements above shield-driven tunnels[J].Chinese Journal of Underground Space and Engineering,2009,5(3):541-545.
[18]王星运,陈善雄,余飞,等.曲线拟合法对路基小变形情形适用性研究[J].2009,30(9):2763-2769.WANG Xingyun,CHEN Shanxiong,YU Fei,et al.Study of applicability of curve fitting methods in small settlement of subgrade[J].Rock and soil mechanics,2009,30(9):2763-2769.
[19]刘松樵.软土扰动地层再固结及其对地铁隧道的影响[D].上海:同济大学,2007:37-42.
