LRB曲线桥震致碰撞效应的非线性分析方法

柳国环，李宏男，陆新征

（1.清华大学 土木水利学院，北京100084；2.大连理工大学 建设工程学部，辽宁 大连116024）

由于伸缩缝的存在，地震激励下相邻联间相对位移一旦大于伸缩缝宽度，则会产生相互碰撞［1－3］。碰撞不仅可能会致使梁体移位过大而塌落，严重的还会导致桥梁发生连续性倒塌。通常可以通过增大伸缩缝来降低碰撞发生的概率，然而过大的伸缩缝会影响路面对平整度的要求。在满足规范的前提下，一种常被工程界采纳的措施为：在桥台与梁体间设置隔震支座，这样可减小地震对梁体输入的能量。2008年10月1日中国新颁布实施的《桥梁抗震设计细则》［4］增加了减隔震桥梁的有关内容。不应否认：隔震后，输入到梁体的地震能量可以得到有效控制。但是，由于隔震支座的引入会使得梁体“变”柔而周期增大，这时梁体更易产生滑移，从而增加了联间的碰撞概率。为此，在概念设计阶段需要考虑伸缩缝处相邻联的自振特性要尽量相近，以充分保证它们在地震作用下的反应具有同步性，从而减小碰撞发生的概率。对于梁高相等且无纵坡的直线型桥而言，在初步设计阶段采用该方法把握结构概念会取得明显效果。但对于曲率不同且有坡道的多联曲线高架桥，尤其是在考虑多维地震动［5］作用下，问题则相对复杂。因此，对这类结构难以用某种指标和（或）概念加以把握，需要具体问题具体分析。建立精细的有限元模型，设置合理的碰撞参数进行数值计算，不失为分析碰撞问题的一种经济且有效之途径。

新建潮汕机场航站楼高架桥全长约940m，其中752m的桥梁结构由曲率不同共9联C50混凝土箱型梁组成，相邻两联桥梁结构交接处和桥台位置设置一道BEJ型浅埋式伸缩缝；工程位于8度地震区，以该工程为背景，考虑设置铅芯橡胶支座（Leader Rubber Bearing，LRB）。采用SAP2000建立全桥空间有限元模型，由25 294个壳单元、140梁单元以及56个接触非线性单元组成。文献［3］在桥梁空间非线性碰撞方面作了重要的推进性工作，但是将其方法通过大型有限元程序实现并应用于实际桥梁工程目前还存在较大困难。

为了便于工程应用，首先发展了一种可适用于体元（例如：壳单元和实体单元）模拟联间碰撞效应的束 缚 面 型 碰 撞 单 元（Constraint－surface Impact Element，CIE），给出了不同以往文献中碰撞单元刚度的合理计算取值，并将该方法应用于工程实际。主要考察了联间的碰撞力、LRB滞回耗能、LRB位移量、基底弯矩、基底弯矩剪力以及碰撞力分别对这些因素的影响。但应该说明，文中只考虑了相邻联桥的轴向正面碰撞，未涉及到非轴向相对运动产生的摩擦等因素。

1 束缚面型碰撞单元

点-点式碰撞单元适用于梁单元间的碰撞模拟。与梁单元相比，考虑壳单元模拟梁体具有以下优点：1）对梁体模拟更为精细，可直接得到更加细部的应力；2）桥墩均可直接与梁体直接连接，避免通过设置刚臂来连接多个桥墩（否则，工程常采用刚臂中间节点与中桥墩相连，端部节点与边桥墩相连）；3）对于隔震桥梁，可以隔震单元将各个桥台分别直接与梁体连接。由此，使得数值模型更加接近物理事实，又能够有效模拟碰撞。为此，提出了一种束缚面型碰撞单元，该单元是对点 点式碰撞单元的发展和推广，然后基于柔度法给出了不同于以往文献的碰撞刚度取值公式。

1.1 束缚面碰撞单元的提出

采用体元剖分后的2根相邻联简易示意图如图1（a）所示。图中f（k）与f（k＋1）分别表示发生碰撞的2个面；mk和mk＋1分别表示相邻联的质量；d（k，k＋1）表示碰撞前间距（伸缩缝宽度）。当每个碰撞面各个节点都归结为一个节点时（例如：采用梁单元模拟梁体），相应的示意图如图1（b）所示。

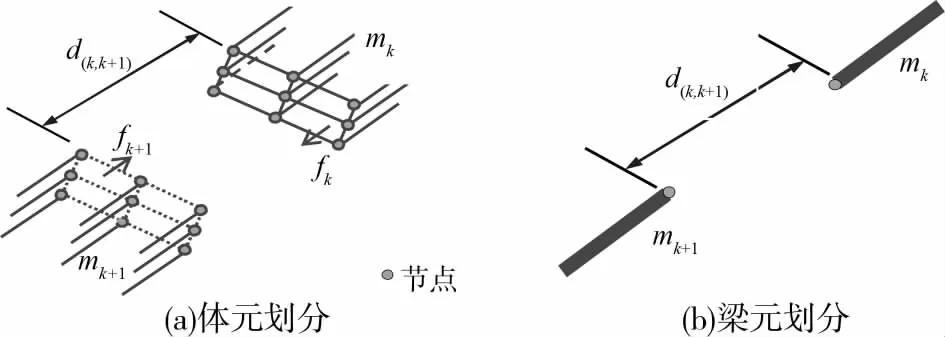
图1 相邻联桥采用不同单元划分的简易图

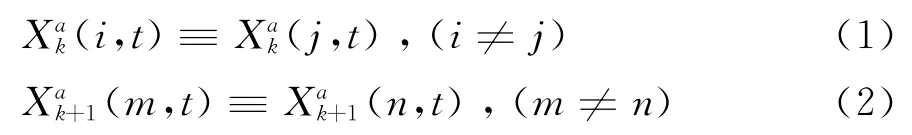
式中，不失一般性，Xak（i，t）表示碰撞面fk第i个节点在t时刻的轴向位移。设节点i和m所在位置分别为fk与fk＋1碰撞接触面的刚度中心，i、m两点通过设置如图2和图3所示的间隙弹簧阻尼单元实现［6－7］。

梁体轴向刚度较大。考虑这一事实，做一个合理的假设：认为面fk与fk＋1碰撞后仍均保持平面，即碰撞面上的各个节点的轴向位移相同。这时，可分别对各碰撞面上节点作如下合理束缚条件（可以通过SAP2000中的constraint功能实现）：

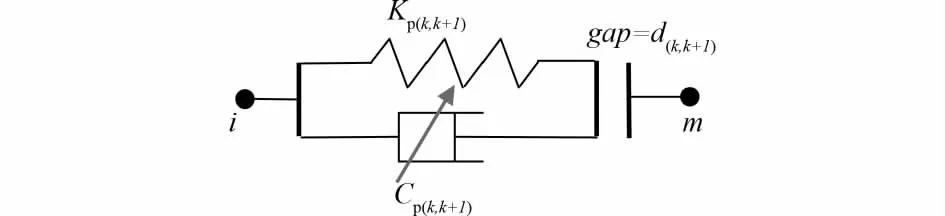
图2 只受压碰撞弹簧单元

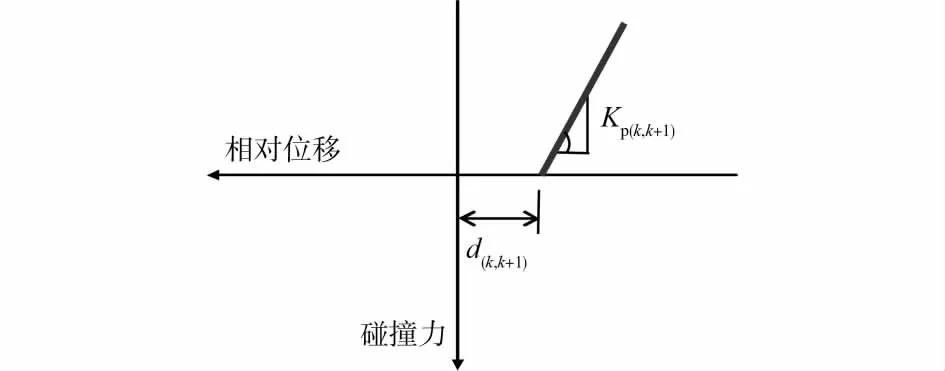
图3 碰撞力与相对位移关系

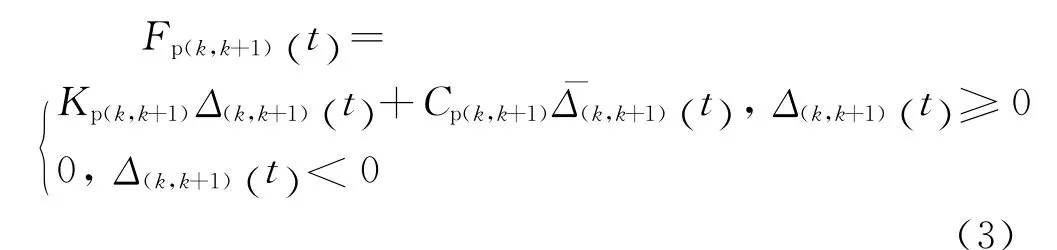
式中：Fp（k，k＋1）（t）、Kp（k，k＋1）和Cp（k，k＋1）分别表示 面f（k）与f（k＋1）在t时刻的碰撞力、碰撞刚度和碰撞阻尼系数；Δ（k，k＋1）（t）为碰撞面间的相对位移，计算表达式如下：

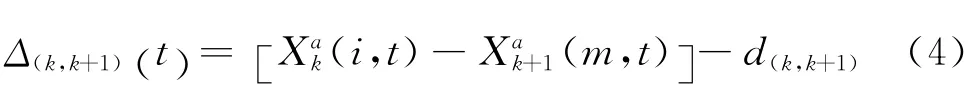
束缚条件式（1）和（2）在本质上起到位移协调的作用。当采用梁单元模拟梁体时，由于只有相邻2根梁2个节点相互接触，式（1）和（2）自然随之不存在。因此，适用于体单元的CIE是对适用于梁单元的点－点式碰撞单元的发展和一般化。容易看出，与用梁单元来模拟梁体不同，若采用体单元并仅在i、m两点设置碰撞弹簧单元而不附加式（1）和（2）作为束缚条件，不仅在物理角度不能够反应面面碰撞这一物理事实，而且在数值计算时由于能量集中于i、m两点而会预见性地出现应力过大现象。

1.2 碰撞单元的刚度取值公式

碰撞单元弹簧刚度Kp（k，k＋1）的有效确定至关重要，不仅直接影响碰撞力，还影响阻尼系数Cp（k，k＋1），本节进一步给出一种新的碰撞单元的弹簧刚度取值公式。首先，总结了文献［3、6－16］对碰撞刚度分别给出了不同的取值方法或建议，如表1所示。

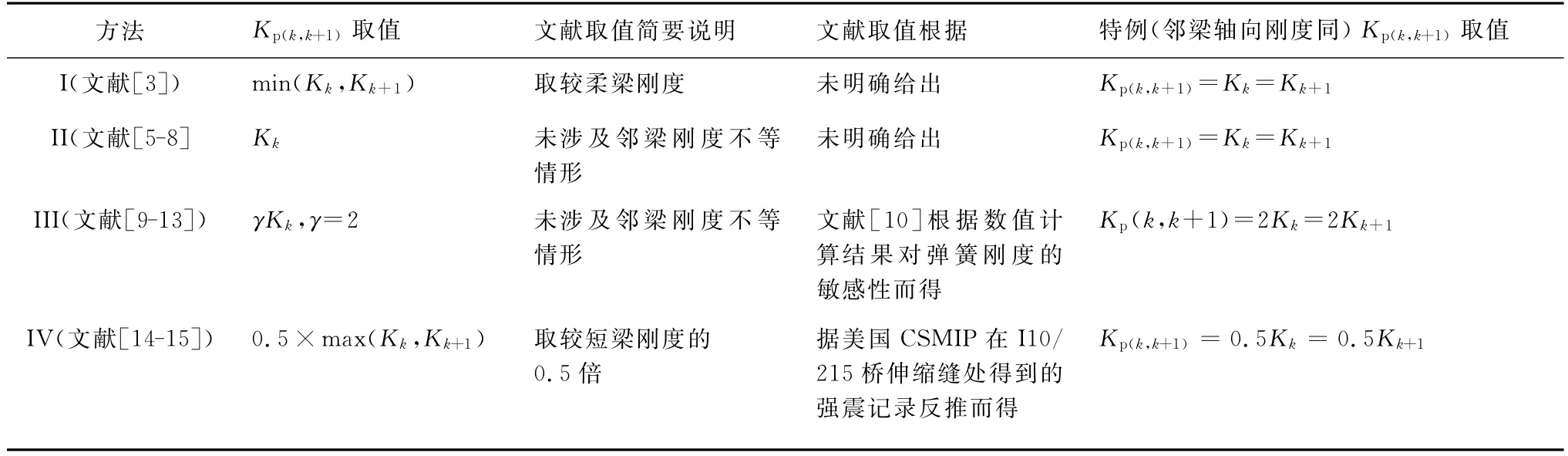
表1 碰撞弹簧刚度取值总结

为充分反应碰撞对结构反应的的影响，以防止邻梁发生相互“嵌入”现象，考虑碰撞发生极为短暂且具有较强的间歇性，时程计算的积分步长很小（一般为10－4s数量级）。这时，可根据结构力学中的柔度法，单位碰撞力作用下的相邻联的相对轴向位移δp（k，k＋1）等于相邻两联的轴向位移代数和，即

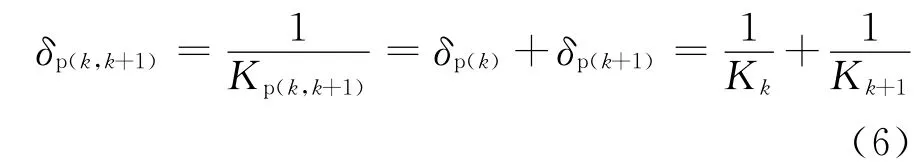
此时根据式（6），碰撞弹簧刚度的取值为

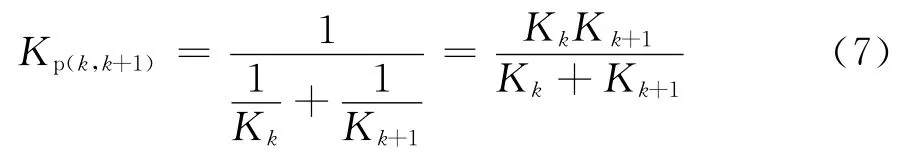
下面，从物理角度出发，将笔者取值方法与表1中取值方法对比，旨在证明笔者方法的合理性和全面性。为此，首先考虑相邻联轴向刚度相同（Kk＝Kk＋1）情形：单位碰撞力作用下的相对轴向位移为每联轴向位移的2倍，即δ式（7）满足这一物理条件，而方法I、II和III均不满足，但方法IV满足；再考虑相邻联轴向刚度不同且相差较大情形（Kk≥Kk＋1）：这时第k＋1对第k联而言相当柔，此时碰撞刚度应为Kk＋1，式（7）满足这一物理条件，而方法IV不满足，但方法I满足。综上所述，建议的碰撞取值公式不仅以柔度法为基础，而且满足物理条件并具有全面性。

1.3 碰撞单元的阻尼系数取值

碰撞单元的阻尼系数Cp（k，k＋1）可根据式（8）［17－20］计算得到。

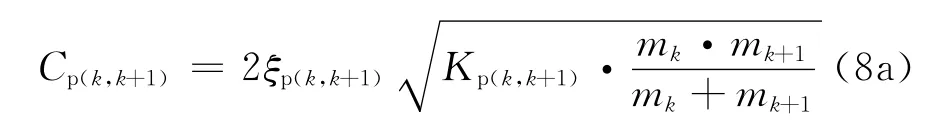
2 动力方程及其相关参数的确定步骤

2.1 动力平衡方程

一离散单元的结构体系，与地面刚性连接。在地震动激励下，带有LRB并考虑碰撞效应的动力平衡方程可表达为：

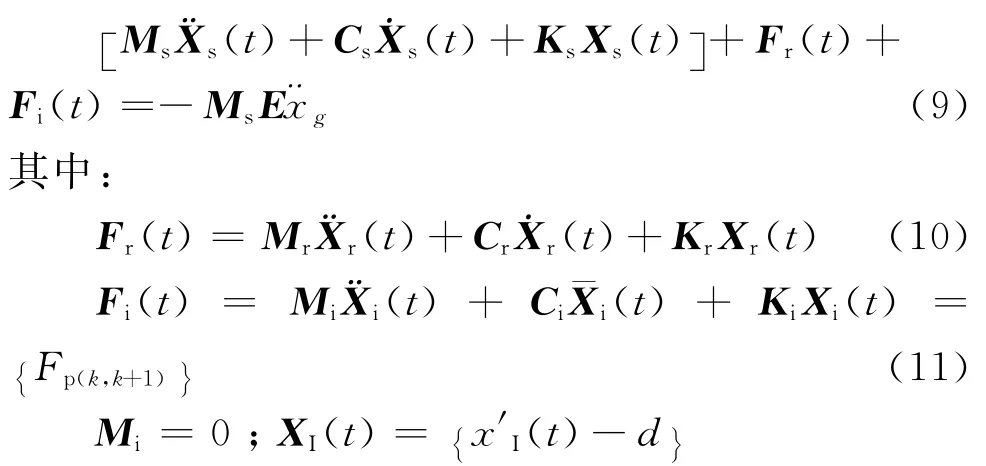
式中：X、和分别为扩大到整体坐标系下的位移、速度和加速度向量；M、C和K分别为整体坐标系下的质量矩阵、阻尼矩阵和刚度矩阵；下标s、r和i分别代表结构自身、LRB以及模拟碰撞效应的碰撞单元；Fr（t）和FI（t）分别表示 LRB滞回力和碰撞力的列向量；E是与Ms同维数的单位列向量，¨xg为地震动加速度时程。基于物理事实，模拟碰撞行为的碰撞单元只涉及碰撞刚度与碰撞阻尼而无质量，故Mi＝0；Fp（k，k＋1）如式（3）所示；x′I（t）为碰撞单元的节点绝对位移，d是碰撞单元间隙。

2.2 相关参数确定步骤

知道各联桥的截面属性、几何属性及伸缩缝宽度，即可根据1.1节所述直接确定碰撞单元的刚度与阻尼取值。如2.1节所述，本节计算并给出各联桥相关属性以及各碰撞单元的刚度与阻尼系数，分别如表2和3所示。

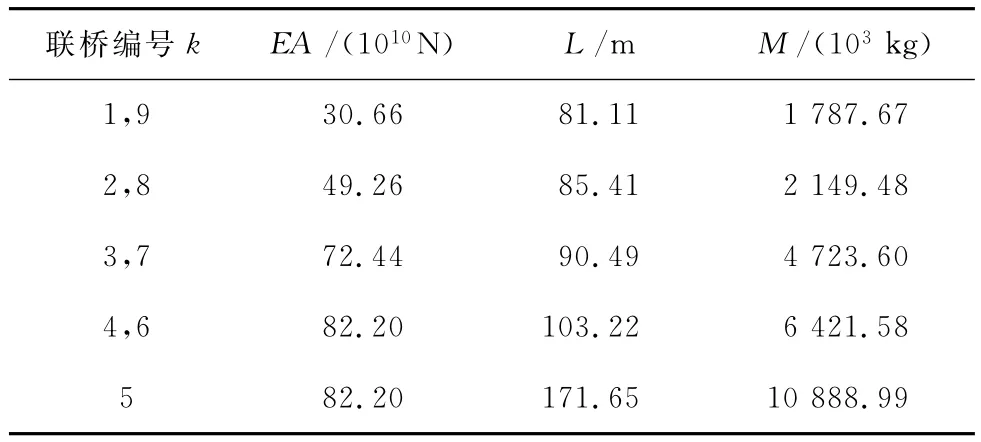
表2 各联桥相关属性统计表

LRB参数确定具体步骤如下：

1）重力作用下作静力分析，提取桥墩的轴力N。据N值对生产公司提供的若干类型LRB进行初步选择，旨在使其能够满足竖向承载能力；

2）确认1）中选择LRB的竖向、侧向刚度以及已确定的碰撞单元的刚度，将其输入到已建立有限元模型并进行模态分析，提取结构圆频率ω；

3）据计算式m＝N／g，计算得到分配到各桥墩墩顶的质量m。再据c＝2ξωm（ξ基于试验给出）计算LRB的阻尼系数c；

4）分别将碰撞单元所需参数输入模型，进行地震时程分析。对比LRB的位移峰值与极限位移，并考察LRB耗能情况；

5）依据规范和（或）规程等具体要求，重复步骤1）～5）。

应该说明，若采用等效阻尼模拟LRB耗能，需要步骤2）和3）。

3 广州潮汕机场航站楼高架桥数值计算与分析

首先建立高架桥有限元模型；然后进行包括重力在内的恒荷载和活荷载作用下的静力分析，依据前文所述步骤和《桥梁抗震设计细则》（JTG／T B02－01－2008）［4］中相关要求，最终选定基于试验给出的LRB；最后，根据第1章所提出的CIE方法将碰撞单元刚度输入有限元模型。

3.1 高架桥有限元模型、LRB参数确定

机场高架桥为半圆曲线型轴对称结构（图4所示），桥梁总长752m，由32（C1－C32）排桥墩共9联C50混凝土连续多跨桥组成。X和Y分别表示垂直和平行于直径方向。高架桥全桥、各联桥有限元模型以及的各联桥的振型分别如图4、图5所示。

图4 高架桥全桥空间有限元模型

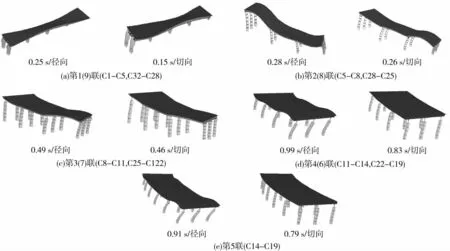
图5 各联桥空间有限元模型及其前两阶振型

由图5可看出，第4（6）和5联桥自振周期较长且介于0.7～1.0s之间，工程处于软土地而容易产生共振，为此在该3联的桥墩与梁体间增设LRB，以期增长自振周期以减小其地震反应。应该说明，为避免共振，可以采用增大该3联桥墩的截面增加钢筋数量的方法提高其抗侧刚度来减小其自振周期。但是，考虑到增加材料、设计时间以及工期要求等因素，相比之下并不经济、省时。第1（9）、2（8）和第3（7）联周期比较短，如果对其也采用隔震支座，则会延长周期反而更接近场地的卓越周期，从而容易引起地基与桥梁共振。

该工程中，梁体、LRB和桥墩三者间的相对布置方式有2种，其有限元数值模拟如图6所示。笔者采用通过图7所示的屈服力Fy、一次刚度K1以及二次刚度K23个参数即可确定的典型双线性LRB滞回模型模拟其滞回耗能。通过反复计算和比较，选用的LRB样本见表4。

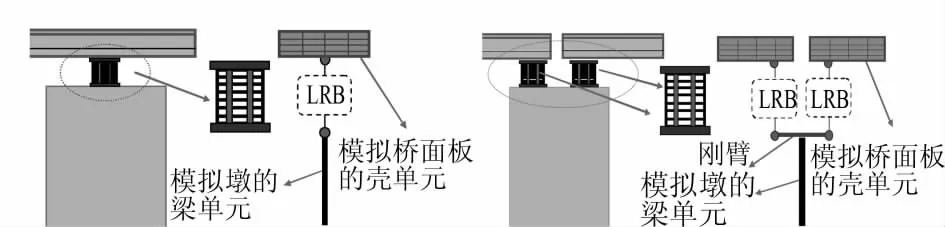
图6 铅芯橡胶支座结构布置及其数值模拟示意图

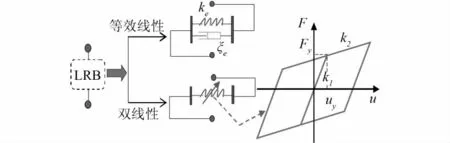
图7 铅芯橡胶支座数值模型

表4 LRB几何尺寸及其性能参数

3.2 隔震后联桥自振特性与地震动选用

设置LRB的联桥有限元模型及局部放大图如图8所示。图9给出了第4（6）和5联桥前2阶振型图，由图中可看出，与设置LRB前相比：1）梁体相对于桥墩更接近平动；2）自振周期增至2倍以上，满足《桥梁抗震设计细则》中条文10.1.6规定。

该工程归于B类桥梁，位于8度地震区，依《桥梁抗震设计细则》中条文3.1.2规定按照9度设防。

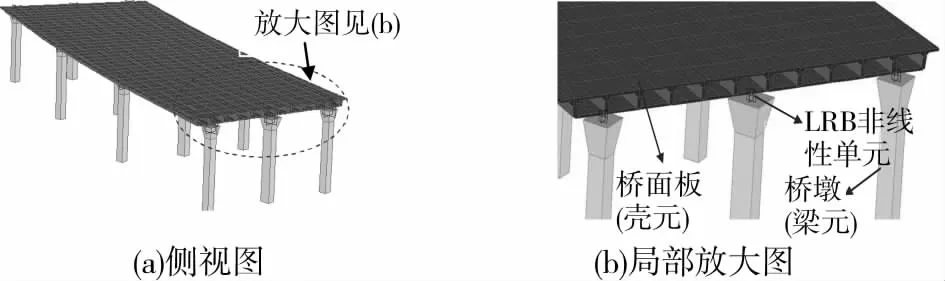
图8 设置LRB的联桥有限元模型

考虑场地类别和结构特性，选用的天然波和拟合的人工波如图10和11所示。应该说明，由于《桥梁抗震设计细则》只规定需要同时考虑三方向地震动输入，但对多维地震动的峰值调整未明确给出规定。为此依据《建筑抗震规范》，对天津波、Parkfield波和人工波三方向峰值调整为1：0.85：0.65。不改变天然波各向原有的频谱，人工波三向频份组成相同。

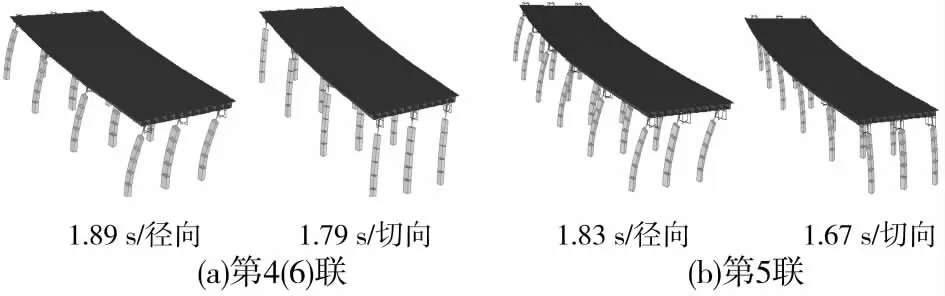
图9 设置LRB联桥的前二阶振型图

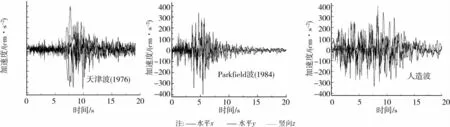
图10 地震波时程

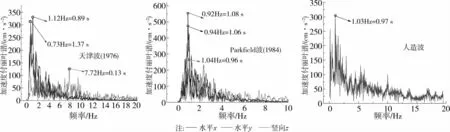
图11 地震波频谱

3.3 结果分析与讨论

限于篇幅有限，通过反复计算和比较只给出天津波（水平x向）在结构x向激励下的计算结果（比较后最大）。

考察碰撞力：各联桥间的碰撞力Fp（k，k＋1）及其频谱Sp（k，k＋1）分别如图12和13。将碰撞力时程曲线与以往文献计算结果相比，在线型（间断式凹凸不平的锯齿形）和幅值2方面具有很好的可比性，说明发展的CIE可行且有效。由碰撞力频谱可看出，从频段角度分析，碰撞力能量曲线由低频向高频段呈现递减趋势，与低频段相比高频段递减趋势更为明显；从频率点角度分析，最大能量均在最低频点（第1频率点）出现。此外，从计算结果来看，碰撞力可归为低频域的宽带反应。

考察LRB滞回耗能及其最大位移：考虑碰撞与否情形下，全桥结构的能量变化如图14所示。图中，Ei、Ed、Eh、Ek、Ee与Eerror依次分别表示全桥的输入能量、阻尼耗能、LRB滞回耗能、动能、势能（弹性变形能）和能量误差。从图15可以看出，不考虑碰撞因素，LRB总的滞回耗能Eh为1.4×107N·m，与考虑碰撞时滞回耗能Eh（2.25×107N·m）相比，被低估接近40%；隔震后的第4（6）和第5联更接近平动，图15给出了两联中位移量最大的2个LRB滞回耗能图，可以看出不考虑碰撞因素的滞回环偏小。此外，考虑碰撞情形下LRB位移量最大量值为230mm，未超过试验给出的极限位移250mm。

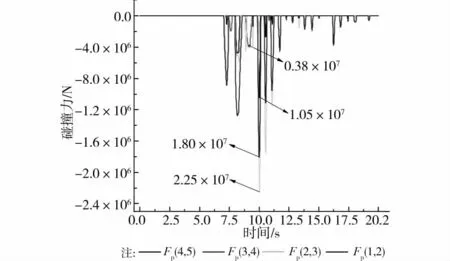
图12 碰撞力时程

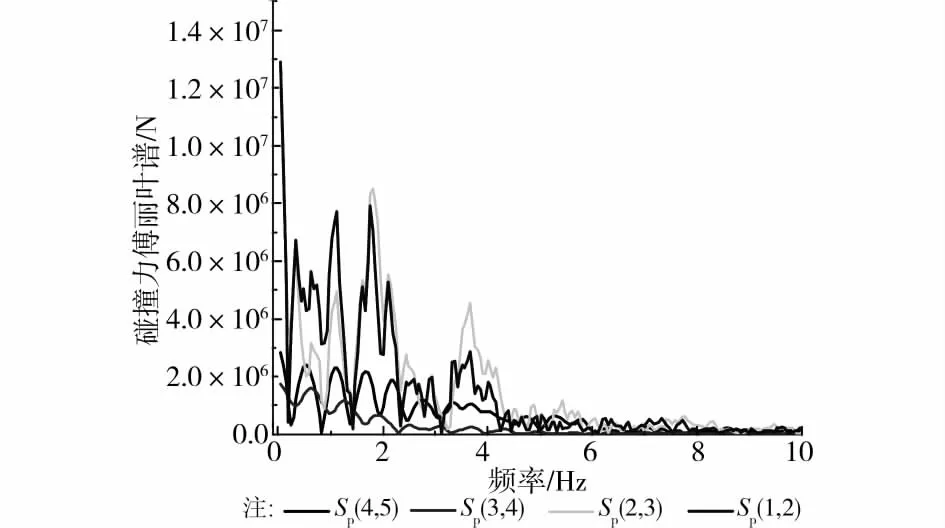
图13 碰撞力频谱

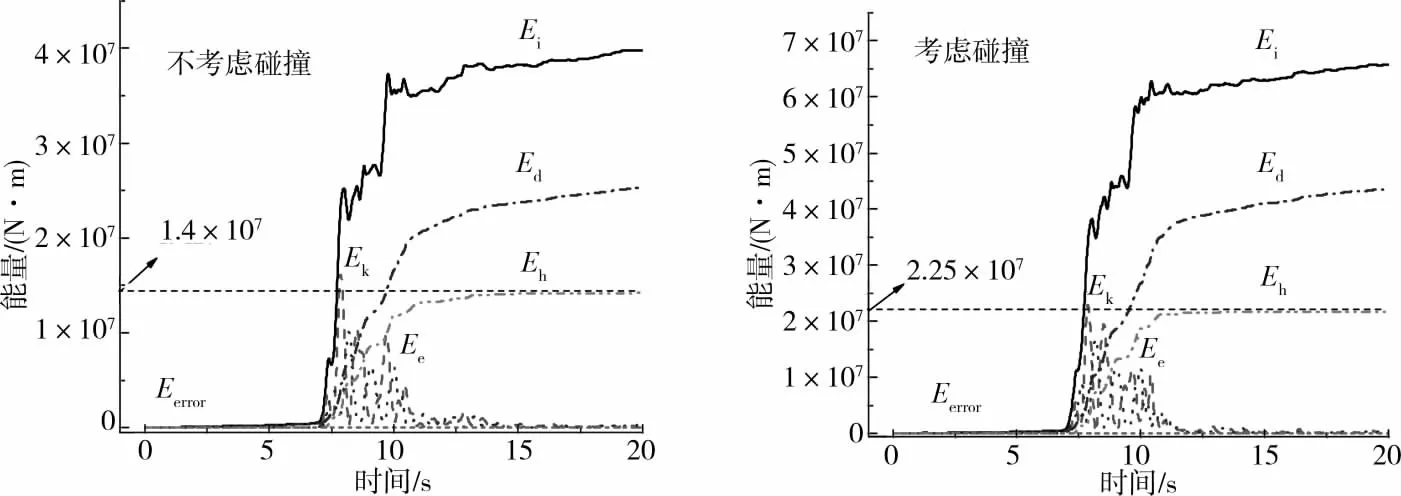
图14 能量时程曲线

考察桥墩基底剪力和弯矩：图16为整个桥梁结构的基底剪力（Vx，Vy）和弯矩（Mx，My）。由图可以看出，不考虑碰撞时的X和Y向的总剪力和弯矩均会被低估；但是，与X向相比，Y向相差更大，这时由于平行于桥直径的Y向产生碰撞概率更大，因而受影响更大。碰撞效应对1～4联桥墩的计算结果影响较大，不考虑碰撞会被低估几倍之多。但是，对第5联桥墩影响相对较小，甚至不考虑碰撞会更加保守，这很能由于第5联处于结构中间对称位置使得碰撞效应会抵消桥墩墩底反应，这说明计算结果与结构的空间几何布置有关。由于篇幅限制，只给出第1和第5联墩底反应时程，如图17所示。

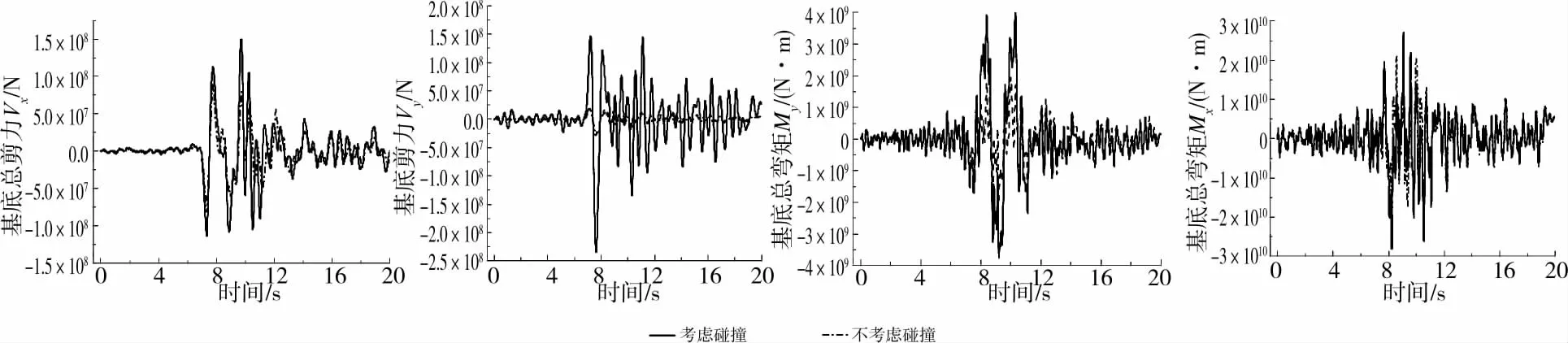
图16 全桥的基底剪力与弯矩

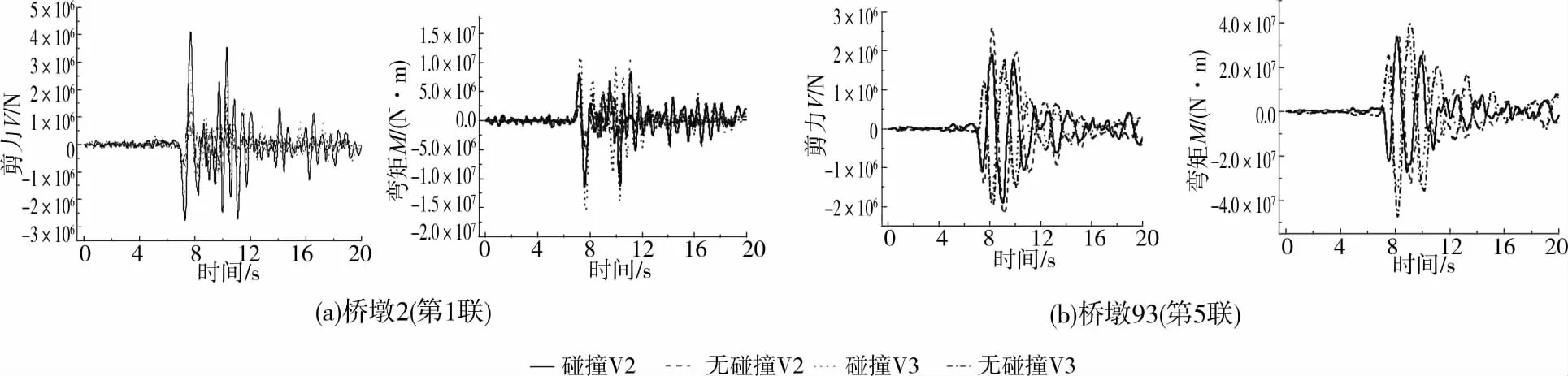
图17 墩底剪力和弯矩时程

4 结 语

以广州潮汕机场航站楼为工程背景，考虑概念设计，满足新颁布的《桥梁抗震设计细则》相关要求，兼顾数值模型的有效性，主要作了如下工作：

1）发展了一种多跨桥联间正面碰撞的束缚面型碰撞单元，该单元是对只适用于梁单元间碰撞模拟的点 点式碰撞单元的发展与一般化。其优点在于：可以考虑采用体元（壳单元、实体单元）模拟联间碰撞效应的同时，避免了传统方法中采用刚臂连接切向多桥墩的简化方法，同时可将切向各桥墩上的非线性单元（例如：LRB）直接与梁体和桥台相连接，从而使得数值模拟更能够接近物理模型。

2）给出了不同以往文献的碰撞单元刚度计算取值公式。与以往取值方法或建议相比，不仅可满足物理条件且更具有全面性。

3）将CIE单元模拟方法通过SAP2000实现并应用于机场航站楼抗震分析，通过碰撞力反应曲线分析，方法是可行有效的。

4）与考虑震致碰撞效应因素相比，不考虑碰撞效应时LRB的滞回耗能会被低估。同时，通过反复数值计算而最终选用的LRB低于试验得到的极限位移250mm，检验了耗能元件的安全性。

5）从总体来看，震致碰撞对结构整体和各联桥墩基底弯矩和剪力会产生不利影响且不容忽视。但同时还应看到，碰撞效应对不同联桥桥墩影响程度不同，甚至不考虑碰撞会更加保守，这与结构以及各联桥的几何位置有关。

［1］范立础.梁桥非线性地震反应分析［J］.土木工程学报，1981，14（2）：41－45.FAN Lichu.Nonlinear earthquake response analysis of beam bridge［J］.China Civil Engineering Joural，1981，14（2）：41－51.

［2］李忠献，岳福青.城市梁桥地震碰撞反应研究与发展［J］.地震工程与工程振动，2005，25（4）：91－98.LI Zhongxian，YUE Fuqing.State of the art of study on seismic pounding responses of urban bridges ［J］.Earthquake Engineering and Engineering Vibration，2005，25（4）：91－98.

［3］Zhu P，Abe M，Fujino Y.Modelling three－dimensional non－linear seismic performance of elevated bridges with emphasis on pounding of girders ［J］.Earthquake Engineering and Structural Dynamics，2002，31：1891－1913.

［4］JTG／TB02－01－2008桥梁抗震设计细则［S］.北京：人民交通出版社，2008.

［5］李宏男.结构多维抗震理论［M］.北京：科学出版社，2006.

［6］Ruangrassamee A，Kawashima K.Control of nonlinear bridge response with pounding effect by variable dampers［J］.Engineering Structures，2003，25：593－606.

［7］Wang C J.Failure study of a bridge subjected to pounding and sliding under severe ground motions［J］.International Journal of Impact Engineering，2007，34：216－231.

［8］Jankowski R， Wilde K，Fujino Y.Pounding of superstructure segments in isolated elevated bridge during earthquakes［J］.Earthquake Engineering and Structural Dynamic，1998，27（5）：487－502.

［9］Jankowski R，Wilde K，Fujino Y.Reduction of pounding effects in elevated bridges during earthquakes［J］.Earthquake Engineering and Structural Dynamics，2000，29（2）：195－212.

［10］Kawashima K，Shoji G.Effect of restrainers to mitigate pounding between adjacent girders subjected to a strong ground motion ［C］／／Proceeding of the 12th World Conference on Earthquake Engineering，2000.

［11］Abdel Raheem S E，Hayashikawa T.Control strategy for seismic pounding mitigation of bridge structures［C］／／IABSE Conference，Helsinki，2008：33－40.

［12］Abdel Raheem S E，Hayashikawa T.Innovative control strategy for seismic pounding mitigation of bridge structures ［C］／／The 14th World Conference on Earthquake Engineering，2008.

［13］Takeno S，Ohno H，Izuno K.Velocity－based design of seismic unseating prevention cable and shock absorber for bridges ［J］.ASCE Structural Engineering and Earthquake Engineering，2004，21（2）：175－188.

［14］Abdel Raheem S E.Pounding mitigation and unseating prevention at expansion joints of isolated multi－span bridges［J］.Engineering Structures，2009，31：2345－2356.

［15］王东升，冯启民，王国新.基于直杆共轴碰撞理论的桥梁地震反应邻梁碰撞分析模型［J］.工程力学，2004，21（2）：157－166.WANG Dongsheng，FENG Qimin，WANG Guoxin.Analysis model of pounding between adjacent bridge girders during earthquakes based on collinear impact between rods［J］.Engineering Mechanics，2004，21（4）：157－166.

［16］王东升，杨海红，王国新.考虑邻梁碰撞的多跨长简支梁桥落梁震害分析［J］.中国公路学报，2005，18（3）：54－59.WANG Dongsheng，YANG Haihong，WANG Guoxin.Seismic analysis of girders falling down in multi－span long simply supported bridges with adjacent pounding effects［J］.China Journal of Highway and Transport，2005，18（3）：54－59.

［17］Jankowski R， Wilde K，Fujino Y.Pounding of superstructure segments in isolated elevated bridge during earthquake ［J］.Earthquake Engineering and Structural Dynamics，1998，27：487－502.

［18］Jankowski R， Wilde K，Fujino Y.Reduction of pounding effects in elevated bridges during earthquakes［J］.Earthquake Engineering and Structural Dynamics，2000，29（2）：195－212.

［19］李建中，范立础.非规则梁桥纵向地震反应及碰撞效应

［J］.土木工程学报，2005，38（1）：84－90.

LI Jianzhong，FAN Lichu.Longitudinal seismic response and pounding effects of girders bridges with unconventional configurations ［J］.China Civil Engineering Joural，2005，38（1）：84－90.

［20］王军文，李建中，范立础.非规则梁桥伸缩缝处的碰撞对地震反应的影响［J］.土木工程学报，2006，39（1）：54－59.

WANG Junwen，LI Jianzhong，FAN Lichu.Effect of pounding at expansion joints on seismic response of irregular girder bridges［J］.China Civil Engineering Joural，2006，39（1）：54－59.

［21］李忠献，岳福青，周莉.地震时桥梁碰撞分析的等效Kelvin撞击模型［J］.工程力学，2008，25（4）：128－133.LI Zhongxian，YUE Fuqing，ZHOU Li.Equivalent Kelvin impact model for pounding analysis of bridges during earthquake［J］.Engineering Mechanics，2008，25（4）：128－133.

［22］Azevedo J，Bento R.Design criteria for buildings subjected to pounding［C］／／Eleventh Word Conference on Earthquake Engineering，Acapulco，1996.

［23］Jankowski R， Wilde K， Fujino Y.Pounding of superstructure segments in isolated elevated bridge during earthquakes［J］.Earthquake Engineering and Structural Dynamics，1998，（27）：487－502.