钢板-砖砌体组合墙梁的试验研究与分析
2012-08-11敬登虎曹双寅
敬登虎,曹双寅,吴 婷
(东南大学 城市与建筑遗产保护教育部重点实验室,南京210096)
钢板 砖砌体组合结构是将钢板通过对拉螺栓约束固定在砖砌体墙上的相应位置,并向内部灌注黏结材料填充内部空隙,最终形成组合梁、柱或者框架,改变主体结构的局部荷载传递路径,主要适用于既有砖混结构房屋承重墙抽除的大空间改造。钢板砖砌体组合结构在实际工程中已得到一定的应用[1-4],但是鉴于当时钢板 砖砌体组合结构的试验与理论研究几乎没有,实际工程应用中的设计方法通常仅考虑钢板的承载力贡献,忽略砖砌体的承载力贡献;并且认为钢板在内部砖砌体以及对拉螺栓的约束下可以达到屈服强度。文献[5]针对钢板 砖砌体组合梁、组合柱进行了试验研究,并考虑了水泥浆和灌注型结构胶两种不同黏结材料;结果表明在不同黏结材料情况下,早期的钢板 砖砌体组合构件的设计方法并不合理,钢板的局部变形影响较大。除此之外,在既有砖混房屋中(尤其是底层)进行部分墙体拆除的大空间改造中,钢板 砖砌体组合托梁与上部墙体之间会存在组合作用;上部荷载在传递过程中由于上部墙体的拱效应,组合托梁上的部分荷载会被卸载。此时,钢板 砖砌体组合托梁与上部墙体之间应作为一个组合墙梁进行设计,类似于钢筋混凝土托梁的墙梁[6]。目前关于钢板 砖砌体组合墙梁的研究未见报道,相关的研究,如型钢梁与上部砖砌体墙之间的共同作用已有学者关注[7-10]。
另外,基于文献[5]的研究结果,此类组合构件采用内部灌注型结构胶的受力性能明显好于水泥浆,实际工程应用中也应优先考虑采用灌注型结构胶填充内部空隙。然而,在具体施工时会遇到操作不规范后,内部钢板与砌体之间的空隙绝大部分被砂浆中渗透的水泥浆填充,使得灌注结构胶的效果很不理想。因此,笔者研究钢板 砖砌体组合墙梁受力性能时,钢板与内部砖砌体之间的黏结材料选择为普通水泥浆,即忽略侧向粘结力(相对灌注型结构胶)对钢板发生局部单向屈曲性能的影响;笔者的研究内容为钢板 砖砌体组合结构受力性能系列研究中的一部分。
1 试验概况
1.1 试件设计
为了与普通钢板 砖砌体组合梁进行对比分析,试件总长取值为2 200mm,支座间距l0为2 000mm。试件顶部采用两点加载的模式,两加载点之间距离为700mm,加载点和邻近支座间距为650mm。鉴于钢板 砖砌体组合托梁的内部砖砌体通常为普通的240mm厚砖墙,试件的内部砖砌体宽度取值为240mm,外贴Q235钢板,钢板与砌体之间有砂浆层(厚度按10mm控制),内部间隙用水泥浆填充。
由于影响墙梁承载力的因素主要有托梁的高跨比、托梁上部墙体高跨比以及钢板的厚度,针对以上影响因素,共设计了5个墙梁试件,试件的其余参数详见表1。其中,厚度为6、8、10mm钢板的实测值分别为5.5、7.9、9.4mm。组合墙梁试件的设计详图见图1。这里需要说明的是,根据文献[11-12]中的钢管混凝土研究结果,对拉螺栓的间距也是钢板局部屈曲的影响因素之一。但笔者暂未考虑此参数,其间距的取值参考已有工程应用中的参数[1]。
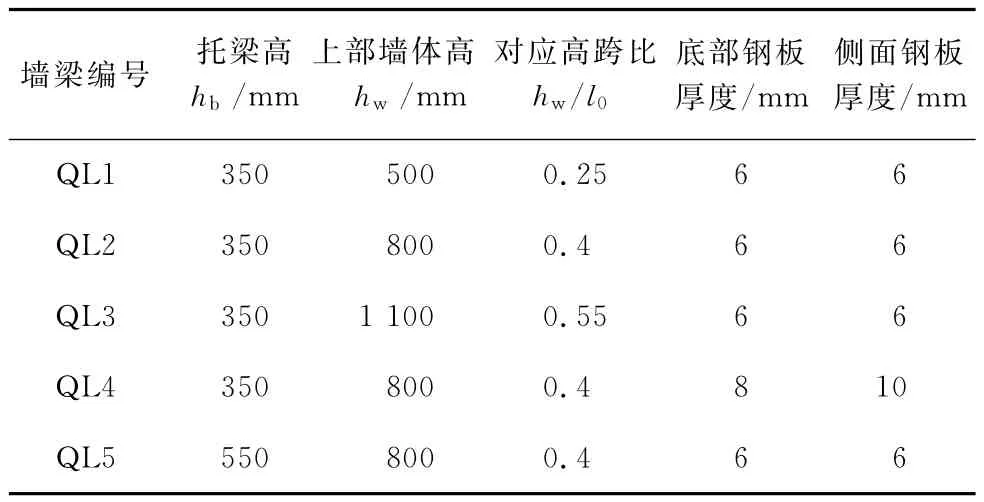
表1 墙梁试件一览表
1.2 试件制作
试件制作由江苏东南特种技术工程有限公司南京分公司协助完成;鉴于上部墙体较高,考虑到运输的难度,故采取了分步制作的方式:先在工地制作好钢板 砖砌体组合托梁部分,然后运到试验室之后,再砌筑上部墙体部分。所用的对拉螺栓规格为M14。
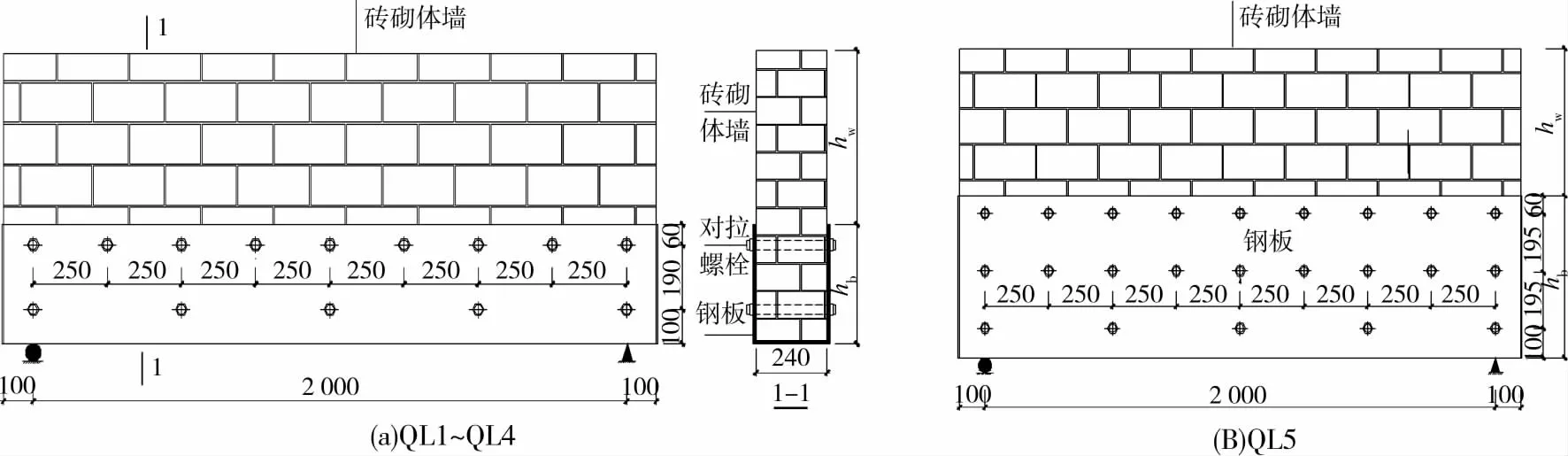
图1 组合墙梁试件详图
1.3 材料力学性能
将Q235钢板制成标准拉伸试件按现行《金属材料室温拉伸试验方法》在万能试验机上进行单轴拉伸试验,实测厚度为5.5、7.9、9.4mm 3组钢板的屈服强度分别为354.4、343.0、326.6MPa;极限强度分别为490.0、450.0、483.5MPa;钢材的弹性模量取值为200GPa。
按现行《砌墙砖检验规则》的要求对砖块强度进行测试,测得砖块的抗压强度平均值为25.5MPa。此外,按照现行《贯入法检测砌筑砂浆抗压强度技术规程》的要求对砂浆强度进行测试,测得砂浆的抗压强度平均值为15.5MPa。根据砖块强度及砂浆强度,可以得出砖砌体的抗压强度为8.20MPa,抗剪强度为0.49MPa。
1.4 加载和测量内容
加载装置示意图见图2,加载使用量程为320t的油压千斤顶。加载模式为单调分级加载,每级拟定为破坏荷载的5%左右,每加一级持荷3min。接近极限状态时连续采集,直至停止试验。在正式加载之前进行预加载,观察应变片数值变化是否合理;如变化异常应进行检查与调整直至达到要求。
本次试验主要测量的数据包括墙梁的承载力、位移、控制截面的应变分布。位移测量采用了电动位移计;应变通过3 815静态应变仪获取。
2 试验结果与分析
2.1 试件受力过程
试件QL1开始加载时变形稳定发展,构件无明显异常现象。荷载达到196kN时,墙体沿灰缝出现阶梯型裂缝,裂缝位于加载点与支座连线的中部;加载至211kN时,砖上出现裂缝;随着荷载增加裂缝不断向支座及加载点处延伸;加载至255kN时,裂缝开展迅速,并伴随着砖块开裂的咔嚓声和螺栓之间钢板与砌体之间剥离声,敲击钢板有空鼓声;加载至313.6kN时,墙体裂缝贯穿,砖上下脱离,西支座上翘明显(图3);加载至352.8kN时,钢板与砌体局部完全脱开(图4);随着荷载的继续增加,钢板与砌体脱离部位增多,钢板的局部屈曲明显可见(图5),并伴随着砌体压碎脱落的声音,直至试件丧失承载力。
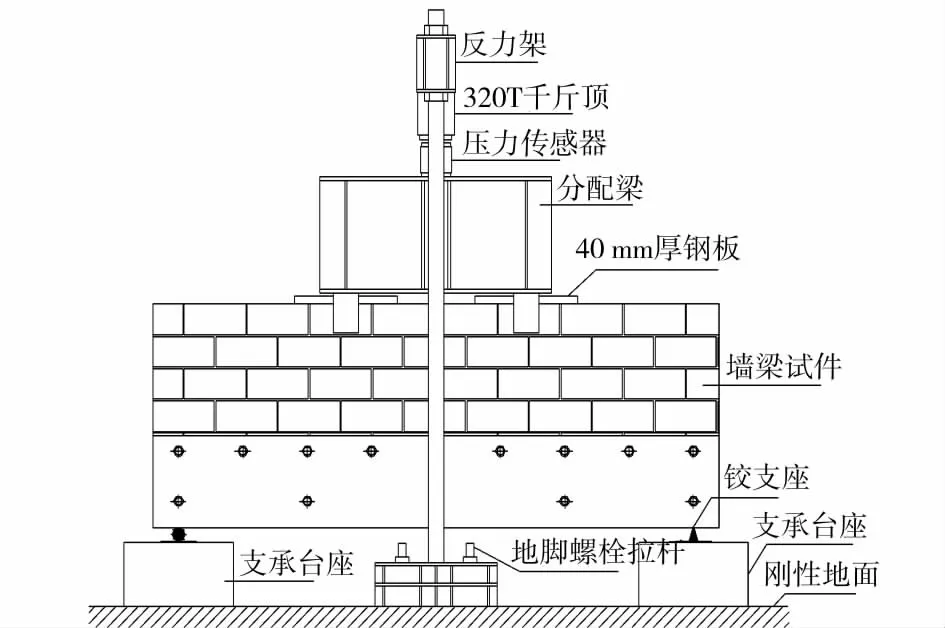
图2 加载装置示意图

图3 试件QL1砌体裂缝
试件QL2加载至235.2kN时,出现第一条沿灰缝的裂缝,位于加载点与西支座连线中部;加载至274.4kN时,出现第一条贯穿砖块的裂缝;随着荷载的增加,裂缝不断发展;加载至294kN时,裂缝发展加快,伴随砖块明显开裂声,敲击钢板有轻微空鼓声;荷载继续增加,钢板多处都有轻微的空鼓声,但是与试件QL1相比,钢板没有出现较为明显的局部屈曲变形,只是轻微与砌体脱开;加载至384kN以后,墙体裂缝开展迅速,瞬间出现若干条新裂缝;接近极限荷载时局部砖块出现压碎,裂缝开展过宽(图6),试件无法继续承载。

图4 试件QL1钢板与砌体脱开

图5 试件QL1钢板局部屈曲

图6 试件QL2砌体裂缝
试件QL3加载至333.2kN时,墙体上裂缝出现,与试件QL1、QL2相比,裂缝出现明显推迟,出现的位置在靠近支座上方,而不是加载点与支座连线的中部;并且,裂缝一旦出现就快速向加载点方向延伸,裂缝宽度在持荷状态时发展到2mm(图7);加载到极限荷载时,上部砌体裂缝发展过大从而发生劈裂破坏,试件丧失承载能力。通过敲击钢板,没有发现钢板空鼓现象。
试件QL4加载至196kN时,在加载点至支座连线中部出现第1条沿灰缝的裂缝;加载至274.4 kN时,出现第1条砖上的裂缝;加载至313.6kN时,裂缝发展加快,数量变多,宽度增大,出现多条贯穿砖块和灰缝的裂缝;加载至450.8kN时,敲击钢板存在轻微空鼓声;随着荷载的增加,裂缝不断发展,加载至极限荷载时,砖块压碎外鼓,无法继续承载。试件破坏的情况见图8。

图7 试件QL3砌体裂缝
试件QL5加载至235.2kN时,在支座与加载点连线中部出现第1条沿灰缝的裂缝;加载至274.4kN时,砖上出现第1条裂缝,之后随着荷载增加,砖上裂缝分别向支座及加载点处延伸;加载至352.8kN时,砖上出现第2条裂缝(图9);加载至372.4kN时,敲击钢板存在轻微空鼓声;加载至548.8kN时,钢板多处出现空鼓现象,且钢板与砌体脱开,但局部屈曲并不明显;随着荷载的增加,墙体沿着两条裂缝发生破坏。与其余4根试件相比,试件QL5墙体上出现了两条主裂缝,且裂缝明显分为两种形态,靠近加载点处裂缝一条近似竖向、1条斜向较陡,裂缝穿过灰缝与砖块;靠近支座处,两条裂缝斜向较缓,沿着灰缝呈阶梯型破坏。

图8 试件QL4砌体破坏

图9 试件QL5砌体裂缝
2.2 破坏形态分析
综合5个试件的受力过程,其破坏形态有一定的共同点。试件的破坏都起源于加载点与支座连线处的砌体部分,托梁部分的钢板出现不同程度的空鼓甚至明显的局部屈曲;随着荷载的增加,墙体裂缝不断发展,最后裂缝贯通,宽度过大,试件无法继续承载而达到承载能力极限状态。同时,由于不同墙梁试件中的主要影响参数不同,导致试件破坏也存在较为明显的区别。
试件QL1上部墙体的高跨比hw/l0=0.25,从破坏形态来看,为剪切破坏中的斜拉破坏,倾角小于45度。墙体中部的主拉应力大于砌体沿齿缝截面的抗拉强度而产生斜裂缝,裂缝沿灰缝呈阶梯型,上端指向加载点,下端向支座处延伸,当主裂缝基本贯通整个墙高时试件达到破坏。除此之外,仅试件QL1中托梁的钢板出现明显可见的局部屈曲,其具体位置见图10,并且两侧呈对称状。
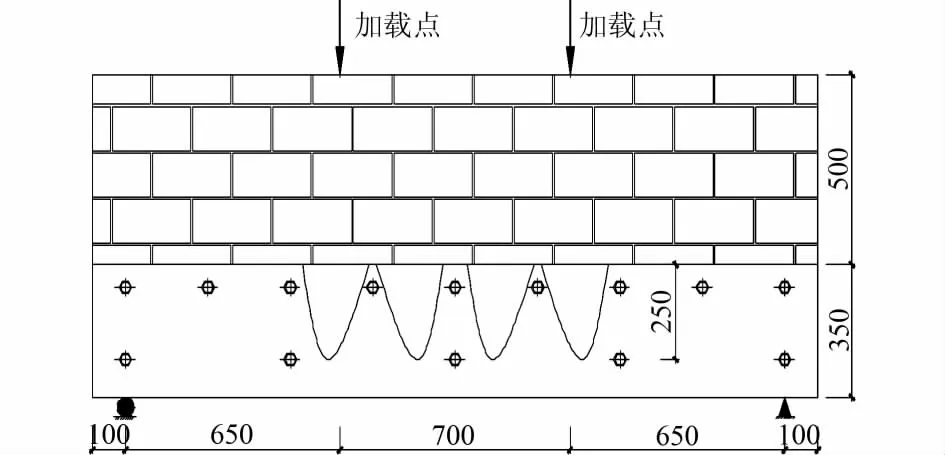
图10 试件QL1钢板屈曲位置
试件QL2上部墙体的高跨比hw/l0=0.40,从破坏形态来看,为剪切破坏中的斜压破坏,倾角一般为55~60度。墙体中部的主压应力大于砌体的斜压强度而产生裂缝,与试件QL1相比,斜裂缝位置比较陡。随着荷载的增加,裂缝既穿过灰缝,亦穿过砖块,砌体沿斜裂缝被压碎剥落而破坏(图11)。

图11 墙体压碎剥落破坏
试件QL3上部墙体的高跨比hw/l0=0.55,从破坏形态来看,为剪切破坏中的劈裂破坏。墙体斜裂缝的形式更陡,裂缝出现的位置也有所不同。裂缝先出现在靠近支座上方,然后向加载点发展,形成下粗上细的裂缝形式,而其他试件裂缝都出现在墙体中部,往两端延伸,裂缝中间粗两头细,且试件QL3的开裂荷载与极限荷载非常接近。试件QL3之所以出现这样的破坏形态,主要原因在于其上部墙体高度相对最大即1 100mm,按倾角55~60度,则上部墙体斜裂缝延伸的最小高度为928mm(小于1 100mm)。因此,使得破坏的裂缝位置出现在靠近支座的上方。
试件QL4上部墙体的高跨比hw/l0=0.40,墙体破坏形式与试件QL2相似,在此不赘述。
试件QL5上部墙体的高跨比hw/l0=0.40,从破坏形态来看,墙体出现了两条主裂缝,且主裂缝的形态为靠近支座处斜拉破坏;靠近加载点处的斜压裂缝,并伴有近似垂直的竖向局部受压裂缝,属于混合破坏形态,并且上部砖块压碎剥落严重(图12)。这是由于试件QL4中的托梁截面最高,使其刚度最大,在竖向荷载作用下托梁的挠度变形相对较小,造成上部墙体的拱效应减弱;竖向荷载不是主要向支座集聚,而是相对比较均匀地向托梁上传递,墙体与托梁的组合作用受到了削弱。当局部受压竖向裂缝形成后,未开裂墙体的高跨比降低,在支座附近容易形成类似于试件QL1的斜拉裂缝。

图12 试件QL5墙体破坏
2.3 承载力及主要影响因素
对于钢板 砖砌体组合构件,由于在破坏的过程中可能存在钢板发生空鼓甚至明显局部屈曲这一特征。因此,钢板 砖砌体组合构件的极限荷载以及钢板发生空鼓和临界局部屈曲时刻对应的荷载都尤为重要。其中,钢板临界局部屈曲时的荷载更是指导加固设计的重要指标之一,毕竟,在组合构件的正常使用极限状态下,不希望钢板出现局部屈曲的现象。然而,钢板在发生临界局部屈曲后,钢板屈曲后的强度仍然能使得组合构件的承载能力继续上升,从而使钢板在发生临界屈曲时对应的状态很难准确地给出[13]。根据本课题组已有的试验结果[14],在钢板局部出现空鼓之后,其对应位置才会逐步进入或者接近临界屈曲状态(当采用灌注型结构胶时)。因此,研究钢板发生空鼓时对应的荷载也非常有意义,但前提必须是内部采用黏结材料填充密实。本文给出试件QL1~QL5中钢板出现空鼓时的荷载,以及极限荷载值见表2,在此不讨论墙体的开裂荷载。
从表2中可以看出,相对试件QL1,试件QL2、QL4和QL5的极限荷载均得到较大幅度提高,其中试件QL2是由于上部墙体增高,使得组合托换梁与上部墙体的组合作用更为有效;试件QL4除了同试件QL2一样的上部墙体外,其托梁的侧板厚度和底板厚度均增加,使得托梁的刚度和承载能力均得到提高;试件QL5是由于托梁的高度增加,也使得其刚度和承载能力有所提高。但是值得注意的是,试件QL3上部的墙体相对最高,但是其极限荷载反而降低,原因是上部墙体发生了位于支座上方的劈裂裂缝。因此,对于钢板-砖砌体组合墙梁构件,适当地增加上部墙体高度,有利于托梁与上部墙体之间拱效应的组合作用增强,但是在集中荷载作用下的过高墙体,会发生墙体的劈裂破坏。
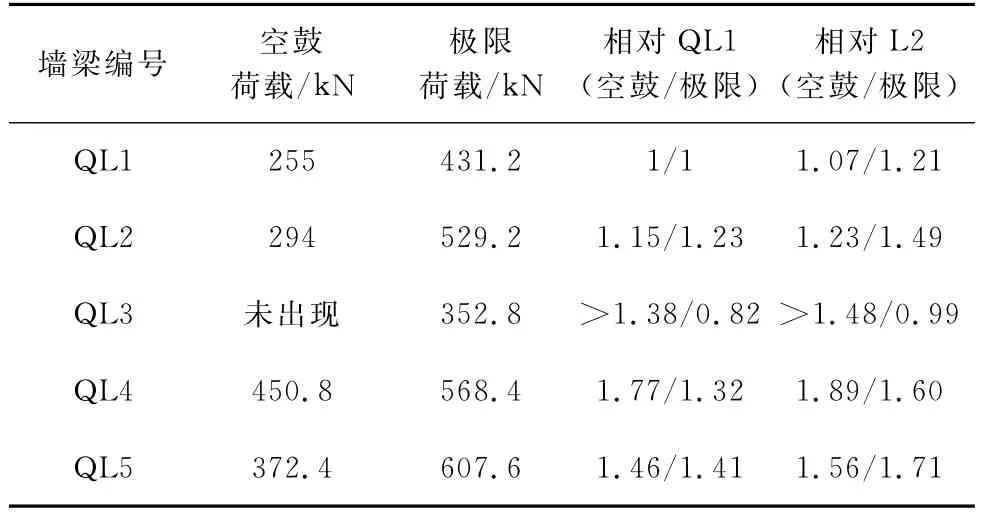
表2 试验荷载值及比较分析
另外,针对空鼓荷载值,试件QL2~QL5相对试件QL1都有较大幅度的提高。并且,在同等组合托梁情况下(QL2与QL3),上部墙体高度越大提高幅度越大;试件QL4提高幅度达到77%,一方面由于上部墙体高度变大组合作用提高,另外侧板的厚度由6mm变为10mm,使得同样边界约束条件下的钢板发生单向局部屈曲的几何条件发生了明显的改变,提高了其临界屈曲应力。此外,试件QL5的空鼓荷载相对QL1也提高了46%,主要原因在于托梁高度的提高,钢板受压区应力水平降低。
在此需要强调的是,试件QL4相对试件QL2,钢板的横截面面积提高了58%,其空鼓荷载与极限荷载分别提高幅度为53%与7%。可见,合理的提高钢板的厚度可以有效地提高空鼓荷载,否则效果并不理想[5]。但是,极限荷载提高非常有限,原因在于本文中的组合墙梁极限状态由上部砌体的破坏控制。
根据上分析,可以很直观地得到影响钢板 砖砌体组合墙梁承载力的主要因素涉及到上部墙体的高跨比、托梁的高跨比和钢板的厚度。
2.4 荷载 挠度曲线
图13为各个试件的荷载与其跨中的挠度曲线。根据荷载-挠度曲线,在受力的全过程中,跨中挠度和荷载的关系基本上分为两个阶段(试件QL3除外),第一阶段挠度与荷载基本成线性关系,挠度发展较为缓慢;然后,曲线有一个比较明显的拐点,进入第二阶段,曲线仍然近似于线性,但随着荷载的增加挠度发展加快。对于试件QL2、QL4及QL5,拐点对应的荷载等级约为极限荷载的60%~75%;试件QL1的拐点对应的荷载等级约为极限荷载的40%;而试件QL3的拐点与极限荷载非常接近。挠度曲线两个阶段的形成主要由于当荷载不是很大时,墙体与托梁共同作用,墙梁整体刚度较大,因此挠度发展缓慢;而加载到后期,即到拐点对应的荷载时,墙体开裂破坏,逐渐退出工作,墙梁的整体性下降,刚度减小,因此挠度发展加快,直至试件破坏。5个试件中,对应于极限状态下挠度最大值为试件QL1的11.22mm;当墙体高度增大时,最大的挠度值即试件QL2的6.44mm。对应于上部墙体开裂或者钢板出现空鼓甚至明显局部屈曲时的挠度值就更小。按混凝土规范要求,正常使用极限状态下构件挠度的限值为1/200跨度,即为10mm。因此,组合墙梁的刚度完全能够满足正常使用要求。

图13 荷载 挠度曲线
2.5 侧板上缘压应变发展
图14 给出了试件QL1~QL5中组合托梁跨中区域侧板上缘平均压应变随荷载的变化趋势,可见在加载初期,侧板上缘平均应变随着荷载的增大基本呈线性的增长。但是到了加载后期,各试件侧板应变出现了拐点,这是由于钢板出现不同程度的空鼓甚至明显可见屈曲(如试件QL1),应变发生突变。突变之后,应变发展明显加快。对于试件QL1,上部墙体高度最小,组合作用相对不明显,荷载从开始主要由托梁承担,因此应变整体发展较为快速;其余试件应变发展相对较为缓慢,一方面主要由于上部墙体与托梁之间组合作用更为明显,托梁作为拉杆抵消一部分压应变;另外由于试件QL4的侧板厚度较大,以及试件QL5托梁刚度增高的原因。此外,试件QL2相对QL1平均压应变发展更为充分,主要由于上部墙体增高组合作用加强,截面受压区高度降低,导致钢板的临界屈曲应力相对提高[12]。
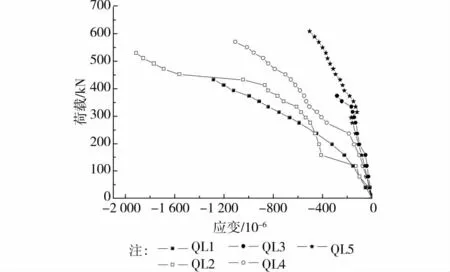
图14 侧板上缘压平均应变 荷载曲线
2.6 截面应变分布和中和轴位置变化
在各试件的中间区域避开螺栓沿钢板截面高度布置了测点,图15给出了钢板应变沿截面高度的分布。从中可以发现,试件QL1的底部钢板进入了屈服状态,试件QL2接近屈服状态,其余构件底部钢板均未屈服。此外,除了试件QL3测试结果有点异常外,其余试件的钢板应变分布沿截面高度符合平截面假定。
比较试件QL1、QL2和QL3(托梁相同)的中和轴位置,可以看出随着墙梁上部墙体高度的增加,托梁中和轴位置逐渐上移。主要原因在于上述试件中拱效应的组合作用加强,作为拉杆的组合托梁轴力依次增大。这一结果进一步验证了增加墙体高度,有利于增加墙梁的整体作用。
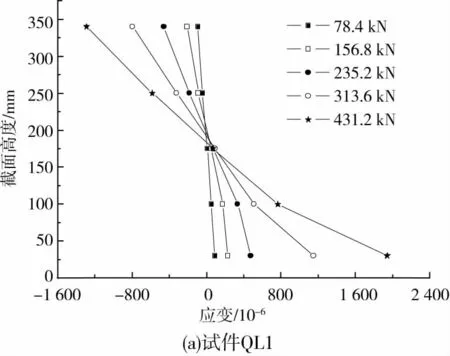

图15 钢板应变沿截面高度的分布
3 墙梁分析与建议
为了更好地理解钢板-砖砌体组合托梁与上部墙体之间拱效应的组合作用。将本文试验得到的结果与文献[14]中试件L2的试验结果进行比较,见表2。试件L2与试件QL1中的组合托梁的几何尺寸相似,钢板的实测厚度为5.6mm,钢板的屈服强度为308.7MPa。
考虑到试件QL1相对试件L2在钢材屈服强度、以及底板宽度(考虑砂浆层的厚度)上的优势,可以认为试件QL1中托梁与上部墙体拱效应的组合作用基本没有发挥。因此试件QL1中整个托梁还是一个受弯为主的普通钢板-砖砌体组合梁,梁底及侧板靠近底板处钢板已受拉进入屈服阶段;受压区钢板出现明显局部屈曲。因此,在上部墙体的高跨比hw/l0≤0.25时,拱效应的组合作用可以忽略。
与试件L2相比,试件QL2、QL4的墙体高度增加,对应的空鼓荷载与极限荷载均提高较大,上部墙体的拱效应形成,托梁与墙体的组合作用开始显现。因此托梁截面的中和轴位置向上移动,侧板上部受压范围的高度减小,侧板虽然出现空鼓,但未见较为明显的局部屈曲。即在上部墙体的高跨比hw/l0=0.4时,拱效应的组合作用明显。
试件QL3从图15(c)中可以看出,托梁的钢板应变很小,相应的应力水平较低;并且钢板未出现空鼓现象。此外,试件QL3的“假定空鼓荷载”相对试件L2提高幅度不低于48%。这就说明在试件QL3中,拱效应的组合作用也很明显,但是其上部砌体破坏控制的极限荷载反而比试件L2还略低。该结果表明集中荷载作用下的钢板-砖砌体组合墙梁中的上部墙体高度应有所限制,防止发生劈裂破坏。按照斜压剪切破坏中的最小倾角55度,假设集中力到墙体边缘的距离为L1,则上部墙体的高度H应满足式(1)。

因此,在集中荷载作用下的钢板-砖砌体组合墙梁中,为了使得上部墙体的拱效应充分发挥,上部墙体的高跨比应满足公式(2)。否则,在墙体端部应增加有效构造措施防止劈裂破坏的发生。
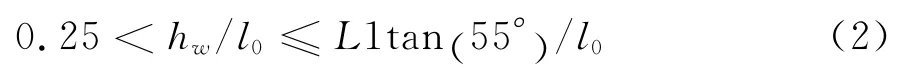
另外,在试件QL5中,上部砌体出现了局部受压竖向裂缝破坏,这一现象与组合托梁的高跨比密切相关。在现行的《砌体结构设计规范》中,限制墙梁中托梁(钢筋混凝土构件)的高跨比不小于1/10,并且认为较大的托梁刚度对承载力、改善上部墙体的抗剪性能和托梁支座上部砌体局部受压性能是有利的;同时,也指出过大的托梁高跨比会使竖向荷载向跨中分布,而不向支座集聚,不利于组合作用充分发挥。虽然试件QL5相对试件L2的空鼓荷载与极限荷载均有很大幅度的提高,但其上部墙体的破坏形态已表明此时托梁的高跨比已经过高。
根据钢梁与砌体之间的组合作用研究成果[10],当上部墙体的高跨比超过0.6时,上部墙体拱支座的应力状态以及钢梁的应力状态已不受其影响。但是,钢梁的刚度与上述应力状态密切相关,并给出了钢梁抗弯刚度相对上部墙体平面内刚度系数K的取值,见式(3)。

其中:Em为砌体的弹性模量,MPa,取值为1 000fm、且不大于20 000MPa;fm为砌体的抗压强度,MPa;t为上部砌体的厚度,mm;E为钢材的弹性模量,MPa;I为钢梁的惯性矩,mm4。当K值越大,说明钢梁相对越弱;反之,则钢梁相对越强。
将公式(3)带入本文的试验数据,且在托梁部分考虑钢板所包裹的砌体对抗弯刚度的贡献,可以得到试件QL1~QL5的系数K分别为108、108、108、100和79。由此可见,为了使得上部墙体与组合托梁之间更好的共同工作,在满足公式(2)的前提下,托梁抗弯刚度相对上部墙体平面内刚度系数K应至少大于79。
4 结 论
对5根钢板 砖砌体组合墙梁进行了试验研究与分析,对钢板 砖砌体组合墙梁在集中荷载作用下的受力性能有了初步的认识。基于试验研究与分析的结果,可以得出以下几点结论。
1)钢板 砖砌体组合墙梁的破坏始于加载点和支座连线部分的砌体;在加载的过程中,托梁中的钢板出现不同程度的空鼓、甚至明显可见的局部屈曲;组合墙梁的极限状态由上部砌体的破坏控制。
2)钢板 砖砌体组合墙梁中的上部墙体破坏形态可以分为以下几种:斜拉破坏、斜压破坏、劈裂破坏和混合破坏(含有斜压、斜拉与局部受压破坏)。具体的破坏形式与上部墙体的高跨比、托梁的高跨比密切相关。
3)钢板 砖砌体组合墙梁的承载能力主要影响因素涉及上部墙体的高跨比、托梁的高跨比和钢板的厚度;组合托梁中的钢板沿截面高度的应变分布符合平截面假定。
4)钢板 砖砌体组合墙梁中上部墙体与托梁之间的组合作用随着上部墙体的高度合理增加而加强,其空鼓荷载与极限荷载都得到相应的提高;但是当上部墙体高跨比过大时,其空鼓荷载仍有较大幅度提高,但极限荷载会因过早地发生上部墙体的劈裂破坏而降低。此外,当上部墙体的高跨比hw/l0≤0.25时,组合作用不明显;并建议上部墙体合理的高跨比应满足公式(2),否则必须采取有效措施防止劈裂破坏。
5)钢板 砖砌体组合墙梁在受力全过程中,跨中的挠度和荷载关系基本上分为2个阶段:第1阶段挠度与荷载基本成线性关系,挠度发展较为缓慢;第2阶段为墙体开裂破坏,墙梁的整体性下降,刚度减小,挠度发展加快。另外,钢板-砖砌体组合墙梁的刚度完全满足其正常使用的要求。
6)当钢板 砖砌体组合墙梁中的托梁抗弯刚度过大时,不利于组合作用的充分发挥,建议钢板 砖砌体组合墙梁在满足公式(2)的前提下,托梁抗弯刚度相对上部墙体平面内刚度系数应至少大于79。
[1]敬登虎,曹双寅,郭华忠.钢板 砖砌体组合结构托换改造技术及应用[J].土木工程学报,2009,42(5):55-60 JING Denghu,CAO Shuangyin,GUO Huazhong.Application of steel plate-masonry composite structure technology for underpinning masonry walls[J].China Civil Engineering Journal,2009,42(5):55-60.
[2]童敏,彭少民.钢 砌体组合结构在砖混建筑改造中的应用[J].武汉理工大学学报,2007,29(增刊Ⅱ):152-156.TONG Min,PENG Shaomin.Application of the steelmasonry structure in a reconstructive engineering of the composite building[J].Journal of Wuhan University of Technology,2007,29(S2):152-156.
[3]熊鸳,胡松.一种用钢结构加固砖混结构的新方法[J].成都大学学报:自然科学版,2006,25(2):88-89,93.XIONG Yuan,HU Song.A new method of using steel structure to reinforce brick and concrete structure[J].Journal of Chengdu University:Natural Science,2006,25(2):88-89,93.
[4]张京街,林文修,张国彬.钢结构在砖混房屋抽墙加固中的应用[J].工业建筑(增刊),2006,36:1069-1070.ZHANG Jingjie,LIN Wenxiu,ZHANG Guobin.Strengthening design of removing bearing-walls in masonry building[J].Industrial Construction,2006,36(S1):1069-1070.
[5]敬登虎,曹双寅,石磊,等.钢板 砖砌体组合梁、柱静载下性能试验研究[J].土木工程学报,2010,43(6):48-56.JING Denghu,CAO Shuangyin,SHI Lei,et al.Experimental study on the static behavior of steel platemasonry composite beams and columns[J].China Civil Engineering Journal,2010,43(6):48-56.
[6]Hossain M M,Rahman M A,All S S.Parametric study of composite action between brickwall and supporting beam [J].Journal of Civil Engineering,2000,CE 28(1):51-67.
[7]Soltis L A,Tuan Y B.Steel supported masonry walls[J].Engineering Journal,1980,17(1):11-13.
[8]Hardy S J.Design of steel lintels supporting masonry walls[J].Engineering Structures,2000,22(6):597-604.
[9]Hardy S J,Al-Salka M A.Composite action between steel lintels and masonry walls [J].Structural Engineering Review,1995,7(2):75-82.
[10]Smith B S,Pradolin L,Riddington J R.Composite design method for masonry walls on steel beams[J].Canadian Journal of Civil Engineering,1982,9(1):96-106.
[11]何振强,蔡健,陈星.带约束拉杆方钢管混凝土短柱轴压性能试验研究[J].建筑结构,2006,36(8):49-53.HE Zhenqiang,CAI Jian,CHEN Xing.Investigation of behavior of square CFT stub columns with binding bars under axial loads[J].Building Structure,2006,36(8):49-53.
[12]LIANG Q Q,Uy B,Liew J.Local buckling of steel plates in concrete-filled thin-walled steel tubular beamcolumns[J].Journal of Constructional Steel Research,2007,63:396-405.
[13]Singer J,Arbocz J,Weller T.Buckling experiments:experimental methods in buckling of thin-Walled structures:shells,built-Up structures,composites and additional topics[M].John Wiley &Sons,New York,2002.
[14]石磊.钢板 砖砌体组合梁受弯性能的试验与理论研究[D].南京:东南大学,2009.
