非晶态木质纳米纤维素机械特性的建模1)

张秀梅 曹 军 仇逊超 Mark A Tschopp Mark Horstemeyer Sheldon Shi

(东北林业大学，哈尔滨，150040) (美国密西西比州立大学) (美国北德克萨斯州大学)

纳米材料的研究是现在的热门研究方向，在现代科学中，人们从大量材料与结构的破坏事件中认识到材料的变形与破坏现象源自材料的微观尺度及原子尺度［1］。将纳米技术引进到木材科学中，极大地扩宽了木材科学的研究领域，使研究深度从细胞水平上升到分子水平。纤维素是世界上可再生、最为丰富的天然生物高分子聚合物，植物的主要结构成分是纤维素，其在木材中的所占比例为40%～50%［2］。木质纳米纤维素是一种由1，4-β-D-葡萄糖甙键链接组成的无支链葡萄糖聚合体，其天然结构是由规则的晶体结构和无规则的非晶态结构构成，晶体结构决定了木材的弹性，非晶态结构决定了木材的灵活性与柔软性，其机械特性由晶体结构与非晶态结构所占的比例来刻画，具有很高的强度以及弹性模量等［3］。自19世纪人类发现木质纤维素中的晶体结构以来，多种不同种类木材的晶体结构已被确定。然而，由于木质纤维素中的非晶态结构的内部原子的排列呈现杂乱无章的分布状态，使得对其机械特征进行相关的研究，存在一定的困难。

笔者利用分子动力学仿真的方法，对木质纳米纤维素中的非晶态结构进行分子建模与拉伸变形仿真研究，通过所建模型仿真研究数据，求得纳观级结构中应力—应变曲线，将其同实验研究方法中的数据相比较，从而预测出材料宏观尺度各特性以及本构关系。对非晶态木质纳米纤维素模型进行研究，对其结构及拉伸变形过程进行细致的分析，填补了国内外对木质纳米纤维素的分子模拟研究的空白，具有重要的意义。

1 建立模型

纤维素是自然界中分布最广、含量最多的一种多醣，由8 000～10 000个D-葡萄糖以β-1，4-糖苷键组成的无支链葡萄糖聚合体，相对分子质量约50 000～2 500 000，相当于300～15 000个葡萄糖基，分子式可写作(C6H10O5)n。1年生或多年生植物，尤其是各种木材都含有大量的纤维素，主要的生物学功能是构成植物的支持组织。自然界中，植物体内约有50%的碳于纤维素的形式存在，一般木材中，纤维素占40%～50%，还有10%～30%的半纤维素和20%～30%的木质素［4-5］。

纤维素的材料力学性能主要依赖于其晶体结构和非晶态结构(无定型结构)的比值，纤维素晶体结构有较强的机械强度，可以作为复合材料的增强基物质;而非晶纤维素展现了重要的黏弹性。反而言之，各种超微结构的形成同时取决于单一分子链的构象特点及其在固态状态下的交互作用。因此，对于木质纳米纤维素的晶体和非晶态结构特点的研究有助于从分子水平理解木材的宏观力学特性，把握木材力学性质的本质性起源。

到目前为止，尚没有成熟的理论模型来描述纳米尺度下木质纤维素的机械特性，对于木质纤维素纳米结构的研究，主要是采用实验的方法对纳米纤维进行提取(酸解法、机械方法、生物菌培育)，再利用实验手段进行分析［6-7］。由于提取到的纳米纤维素的几何尺寸微小，因此对实验测定的设备和测试技术要求较高，仅仅通过实验方法并不能完全了解纳米材料的微观结构、性能及内在机制。随着计算机技术的进步，计算机模拟已广泛应用于材料科学的研究中，分子动力学模拟可以弥补实验的不足，获得有关的原子运动细节，有效地澄清实验现象，揭示内在机制。

采用美国Accelrys公司开发的Materials Studio软件建立非晶态木质纳米纤维素结构的分子模型，应用周期性边界条件，并提取初始状态的原子坐标、晶格长度、速度分布、环境状态等数据，图1为木质纤维素单体的分子结构。

图1 木质纤维素单体的分子结构

图2为微/纳木纤丝非晶态结构的分子模型，其中图2b为经过能量最小化后的分子模型。

木质纳米纤维素结构是由一些长短不等的纤维素分子链聚集成的，在大分子链排列最致密的地方，分子链规则平行排列，定向良好，反映出一些晶体的特征，所以被称为纤维素的结晶区，分子链与分子链间的结合力随着分子链间距离的缩小而增大。当纤维素分子链排列的致密程度减小、分子链间形成较大的间隙时，分子链与分子链彼此之间的结合力下降，纤维素分子链间排列的平行度下降，此类纤维素大分子链排列特征被称为纤维素非晶态结构(有时也称作无定形区)。结晶区与非结晶区之间无明显的绝对界限，而是在纤维素分子链长度方向上呈连续的排列结构。

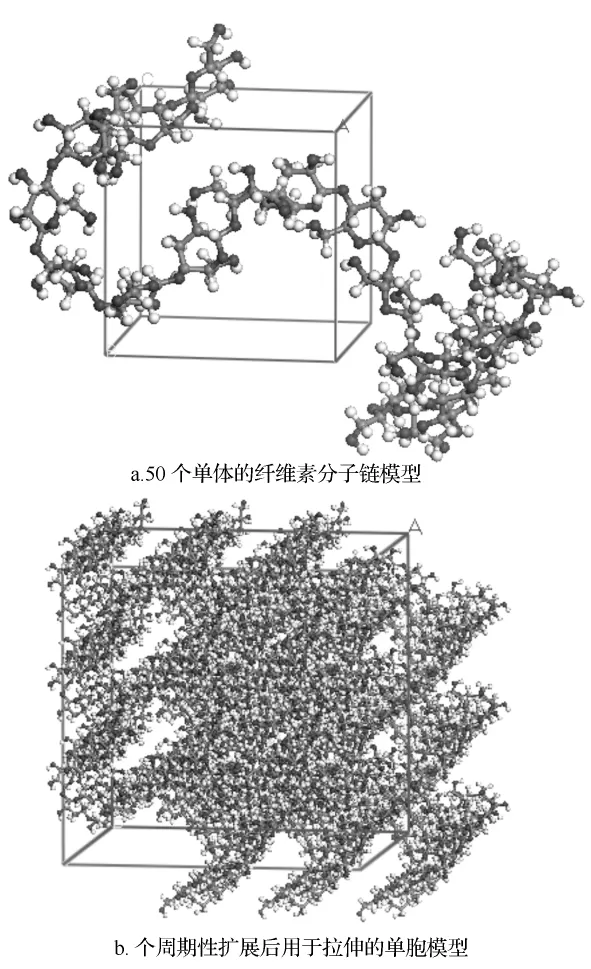
图2 构建的木质纳米纤维素非晶态结构的分子模型

对纳米木纤维非晶态结构进行建模时，首先建立一个单元的无规则晶胞，为了后期验证不同链长对于建模仿真的机械特性的影响，所建模型中定义了3种不同长度的纤维素分子链，分别是由20、50、100个葡萄糖单体连接而成。定义纤维素分子链排列的致密程度为1.5 g/cm3，图2a所示为100个葡萄糖单体构成的纤维素分子链，然后沿着x、y、z方向进行周期性拓展，从而构建出3×3×3的木质纳米纤维素非晶态结构的模型。由于生成的无规则单胞，分子可能不是等价地分布在单胞中，从而造成了真空区，为了矫正此现象，就要进行能量最小化来优化此模型。图2b为周期性扩展后并进行能量最小化后得到的分子模型，也是本研究用于拉伸变形仿真模拟的模型。

2 分子动力学

2.1 运动方程

分子动力学是一套分子模拟方法，依靠牛顿力学来模拟分子或原子的运动，通过求解各分子或原子的运动方程，得到其不同时刻的位置、动能和能量等，从而统计出材料的宏观热力学量和其他宏观性质。

分子动力学的研究对象是由一定量的分子或原子组成的系综。假设在包含有N个原子的系综中，定义 r1，r2，…，rN为原子的位置矢量，U(r1，r2，…，rN)为描述N个原子间的作用力势能函数，Fi=-▽riU(r1，r2，…，rN)为第 i个原子的受力，则用于描述第i个原子运动的牛顿方程为：

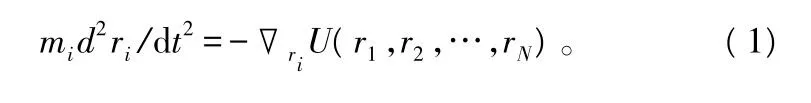
式中：mi为第i个原子的质量。

在实际计算中，根据加载情况给出相应的边界条件与起始条件，系统在此时的状态是强加的。它必须通过很多松弛步，逐渐达到真实的平衡位置，即满足运动微分方程及初始与边界条件，而达到总势能最小的位置。为了得到较精确的结果，显然要求从前一步到下一步的递推关系给出的算法能进行高效率的计算，并且计算格式在数值上是稳定的。常用的有限差分算法有Verlet算法、Leap-frog算法、Velocity Verlet算法和 Beeman’s算法［8］。

2.2 初始条件和边界条件

在进行分子动力学仿真前，需要对原子的空间位置ri、初始速度vi进行初始化。本研究利用Materials studio软件构建木纤维非晶态纳米结构的分子模型。然后通过Matlab软件将该模型转换为Lammps可读取的文件，从而获得了各个原子的空间位置与初始速度，实现了原子的初始化。

在分子动力学仿真中，通过选取一定的边界条件，可以用有限的模拟区间得到具有宏观尺寸的物理结构与材料的机械特性。本研究选取周期性边界条件，引入周期性边界条件的作用是：在原子的运动过程中，若有一个或几个粒子跑出模型，则必有一个或几个粒子从相反的界面回到模型中，从而保证该模拟系统的粒子数恒定;采取最近镜像方法计算原子间的作用力，使得所模拟系统边界处的原子的受力比较全面，从而消除了边界效应。

2.3 反应性力场

本研究中，利用反应性力场(ReaxFF)进行拉伸变形仿真，模拟原子间的相互作用。反应性力场是加州理工 Adrivan Duin、William A.GoddardⅢ等人开发的力场，它是结合鲍林键长键能关系得到的半经验势，呈现出简单、快速、放热反应势能的反应性力场，对描述键之间的断裂与再结合很有利。大多数高能材料反应区域比较宽，反应时间比较长，由于过分消耗计算资源，模拟原子间的稳定爆破与凝聚几乎是不可能的，为此产生了反应性力场经验键级势能，并且被延伸到扭转效应，使它可用于依赖外部环境的原子间的相互作用，适合模拟木质纳米纤维素非晶态结构的分子模型在拉伸变形过程中键之间的各种变化［9-11］。反应性力场将整个系统的能量划分为几个不同的能量部分，如下式所示：

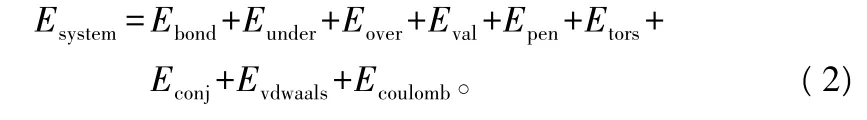
式中：Ebond为共价相互作用能;Eunder和 Eover为对等/过等能;Eval为键角相互作用能;Epen为补偿能;Etors为二面角扭转能;Econj为键结合能;Evdwaals为范德华作用能;Ecoulomb为静电作用能。可知，反应性力场由原子内相互作用和原子间相互作用两大部分构成，即力场的势能包括成键和非键相互作用，其中范德华作用能和静电作用能属于非键相互作用势能。

2.4 系综

分子动力学仿真需要在一定的系综下进行，所谓系综是指在一定的宏观条件下，大量结构与性质完全相同的、处于各自独立、各种运动状态的系统的集合。系综用于研究系统的微观状态与宏观热力学性质的对应规律。分子动力学仿真的不同系综有：仿真系统中原子数N、体积V和能量E都保持不变的微正则系综(NVE);仿真系统中原子数N、体积V和温度T都保持不变的正则系综(NVT);仿真系统中原子数N、温度T和压力P都保持不变的等温等压系综(NPT);以及仿真系统中原子数N、压力P和焓值H都保持不变的等焓等压系综(NHP)。

本研究对能量最小化后的纳米木纤维非晶态结构的分子模型，在微正则系综(NVE)条件下，实现热平衡仿真。对热平衡仿真后的模型，在等温系综条件下，进行拉伸速率恒定的拉伸变形仿真。

3 仿真模拟

3.1 仿真步长

分子动力学仿真中，最重要的工作为如何选取合适的积分步长，在节省时间的同时也保证计算的精确性。太长的步长会造成分子间的激烈碰撞，体系数据溢出;太短的步长会降低模拟过程搜索相空间的能力。本研究选取两种积分步长，即Δt1=0.5 fs，Δt2=1 fs，观察不同积分步长下，系统温度、总能量以及动能、势能的波动情况，从而确定积分步长的选取。两种积分步长模型温度的波动情况如图3所示，其中图3a选取的积分步长为Δt1=0.5 fs，图3b选取的积分步长为Δt2=1 fs。

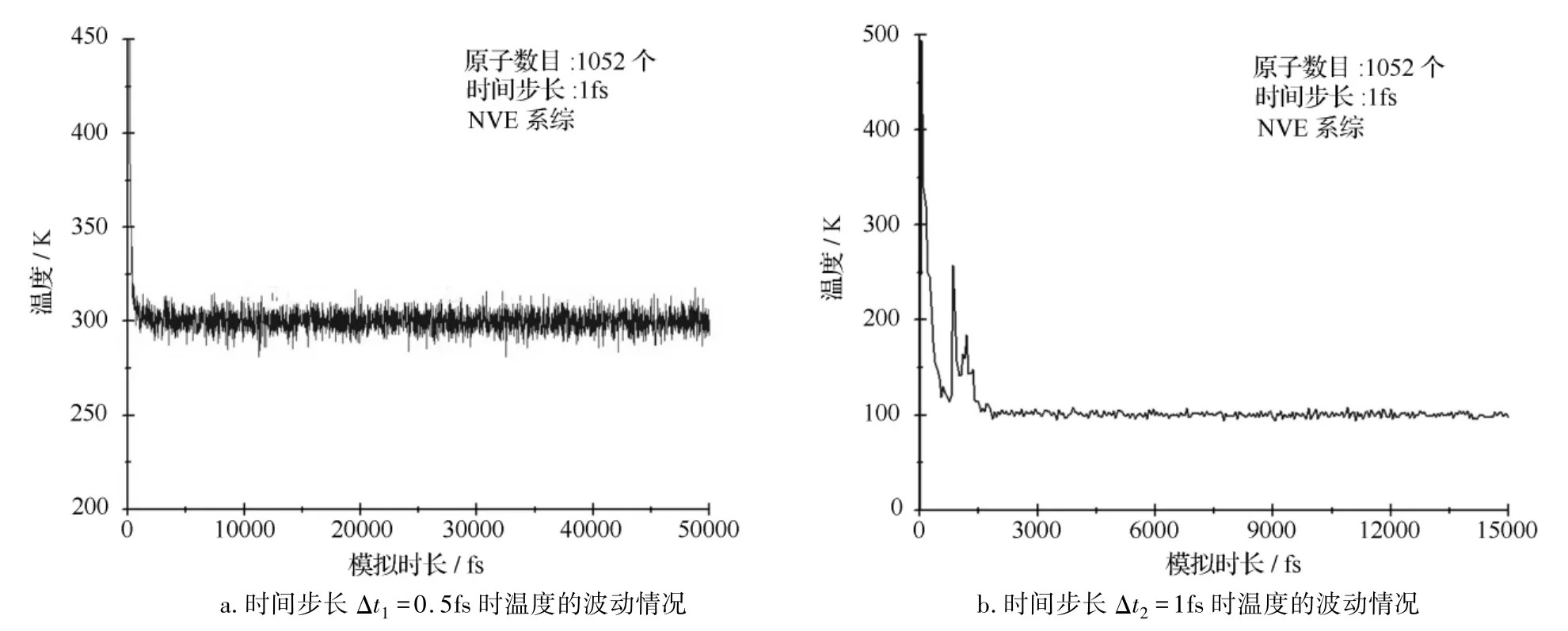
图3 两种积分步长系统温度的波动情况

热平衡的仿真在基于反应性力场的微正则系综(NVE)条件下进行，由图3可知，在积分步长选取为Δt1=0.5fs的条件下，模型未经过震荡达到了热力学平衡态;而在积分步长选取为Δt2=1fs时，模型经过多次震荡才趋于平衡。模型的能量(总能量、动能及势能)的波动情况如下图4所示，其中图4a选取的积分步长为Δt1=0.5fs，图4b选取的积分步长为 Δt2=1fs。

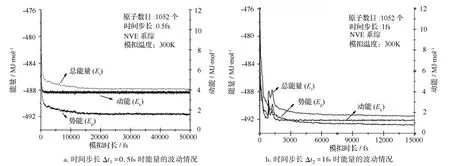
图4 两种积分步长系统总能量、动能及势能的波动情况

能量变化的仿真在基于反应性力场的微正则系综(NVE)条件下进行，由图4可知，在积分步长选取为Δt1=0.5fs的条件下，模型的能量(总能量、动能及势能)在没有经过明显震荡的情况下较快速的达到平衡态;而在积分步长选取为Δt2=1fs的条件下，系统的能量(总能量、动能及势能)有明显的震荡，并且在原子间距离过近时，易发生原子回弹现象。因此，在今后采用基于反应性力场的分子动力学仿真研究中，应选取0.5fs的积分步长。

3.2 物理与机械特性

通过计算模型的密度、弹性模量、剪切模量以及泊松比，来反映构建的木质纳米纤维素非晶态结构的分子预测模型的物理与机械特性，将计算得到的数据与在文献中采用实验研究方法获得的结果进行比较，从而判断该预测模型的精准性，比较结果如表1所示。可以观察到，对构建的木质纳米纤维素非晶态结构分子模型，采用基于反应性力场的分子动力学进行原子间相互作用的仿真，从而计算得到木纤维非晶态结构纳观尺度的物理与机械特性，与文献［12］中给出的相关特性值十分相似。因此，利用构建的理想模型，采用基于反应性力场的分子动力学模拟原子间的作用，对纳米木纤维非晶态结构进行进一步的相关研究是可行的，并且研究结果是完全具有可信度的。计算理想模型得到的相关特性值与文献中的相关特性值存在细微差异的原因是：构建的理想模型是均质化的，而采用实验研究方法获得的微/纳木纤丝，其纤维素分子链、晶体与非晶态结构的分布均是非均质的;并且采用实验研究方法获得的微/纳木纤丝可能会含有一定的湿度及杂质，从而造成了细微的差异。

表1 微/纳木纤丝非晶态结构的物理与机械特性

3.3 拉伸仿真

在对纳米木纤维非晶态结构的分子模型进行基于反应性力场分子动力学拉伸变形仿真的过程中，只对x轴方向施加单轴应力，而保证由y轴、z轴构成的二维平面的应力为0。拉伸仿真是在模型经过能量最小化及热平衡仿真后，在等温系综下进行的，分子动力学计算使用开源代码程序LAMMPS。拉伸仿真前后的原子结构如下图5所示。

图5 拉伸仿真前后的分子结构

拉伸变形仿真的过程中，选取的温度为T=100 K，低于玻璃化转变温度;选取的拉伸速率为1010s-1，仿真中的原子数为28 404个。图5a为拉伸仿真前的原子结构，图5b为拉伸仿真后的原子结构，可以看出，沿拉伸x方向出现拉长现象，而y和z方向则出现长度缩减，正是由于采用ReaxFF力场进行仿真研究，结果符合实际拉伸过程中的变化。

对木质纳米纤维素非晶态结构分子模型进行基于反应性力场分子动力学拉伸变形仿真后，绘制其应力—应变曲线，如图6所示。

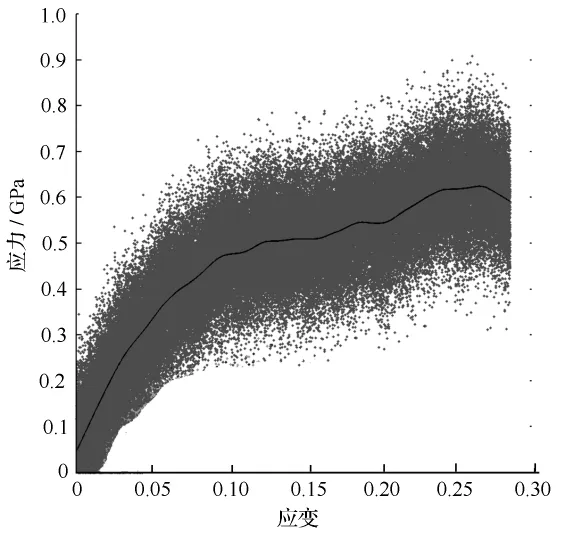
图6 应力—应变曲线

图6中的黑色曲线为原子受到x轴方向施加的单轴应力的瞬间分布情况的平均应力响应曲线。可以观察到，纳米纤维素非晶态结构分子模型首先经历弹性变形，接着在0.5 GPa左右出现应力平台，平台期的应变长达35%，在平台期结束后继续拉伸时，应力重新上升到0.6 GPa左右，并发生弹性屈服。拉伸仿真后绘制的应力—应变曲线与在文献中采用实验研究方法获得的应力—应变曲线具有相同的变化规律。

4 结论

首先对木质纳米纤维素非晶态结构进行周期边界条件建模，然后对该模型进行能量最小化和热平衡处理，利用基于反应性力场对模型进行拉伸变形仿真，最终绘制出预测模型的应力—应变曲线。通过对构建的纳米木纤维非晶态结构的热平衡及能量的仿真，确定了在今后的采用基于反应性力场的分子动力学仿真研究中，应选取0.5fs的积分步长;计算模型的物理与机械特性，并与采用实验研究方法获得的相应特性进行比较，表明了采用本研究方法对木质纳米纤维素非晶态结构进行进一步的相关研究是可行的，并且研究结果完全具有可信度;对模型的应力—应变曲线进行分析，表明了采用本研究方法与采用实验研究方法获得的应力—应变曲线具有相同的变化规律。本研究属于交叉和前沿的研究，填补了国内外对木质纳米纤维素非晶态结构的分子模拟研究的空白，对提高木材以及木质复合材料从微观到宏观的力学性能认识、完善木材纳米微观力学具有重要促进作用。预期研究成果可用于各种工程产品，为终端客户提供科学试验数据以及可视化的机械特性效果，推动纳米技术在木材科学领域的研究，在新的层次上验证可持续发展的理论。

［1］黄克智，吴坚，黄永刚.纳米力学的兴起［J］.机械强度，2005，27(4)：403-407.

［2］邱坚，李坚.纳米科技走进木材科学［J］.国际木业，2003(1)：10-11.

［3］Lima M，Borsali R.Rodlike cellulose microcrystals：Structure，properties，and applications［J］.Macromolecular Rapid Communications，2004，25(7)：771-787.

［4］Kamide K.Cellulose and cellulose derivatives：molecular characterization and its applications［M］.The Netherlands：Elsevier，2005.

［5］O'Sullivan A C.Cellulose：the structure slowly unravels［J］.Cellulose，1997，4(3)：173-207.

［6］Yoshiharu N，Junji S，Henri C，et al.Crystal structure and hydrogen bonding system in cellulose Iβfrom synchrotron X-ray and neutron fiber diffraction［J］.Journal of the American Chemical Society，2003，125(47)：14300-14306.

［7］Samira E H，Yoshiharu N，Jean L P，et al.The shape and size distribution of crystalline nanoparticles prepared by acid Hydrolysis of native cellulose［J］.Biomacromolecules，2008，9(1)：57-65.

［8］Frenkel D，Smit B，Ratner M A.Understanding molecular simulation：from algorithms to applications［M］.Orlando，USA：Academic Press，1996.

［9］Hasan M A，Sagar A P，Adri C D，et al.Reactive molecular dynamics：numerical methods and algorithmic techniques［J］.International Journal of Mechanical Sciences，2010，22：1-29.

［10］Kimberly C，Adri CD，William A G.ReaxFFreactive force field for molecular dynamics simulations of hydrocarbon oxidation［J］.The Journal of Physical Chemistry A，2008，112(5)：1040-1053.

［11］Adri CD，Siddharth D，Francoins L，et al.ReaxFF：A reactive force field for hydrocarbons［J］.The Journal of Physical Chemistry A，2001，105(41)：9396-9409.

［12］Chen W，Lickfield GC，Yang CQ.Molecular modeling of cellulose in amorphous state.Part I：model building and plastic deformation study［J］.Polymer，2004，45(3)：1063-1071.