孑遗植物水松种源高径生长的空间变异及其分形特征1)

吴则焰 刘金福 洪 伟 郑世群 何中声

(福建农林大学，福州，350002)

树木种源生长特性在不同空间位置存在明显差异，即树木种源生长具有空间变异性。研究树木种源生长特性的空间变异及其趋势，对种源区划分、种子调拨以及优良种源的选择具有重要意义［1］。传统的统计学方法不能定量地描述其随机性和不规则性，自20世纪90年代初马克明、祖元刚等人将分形(Fractal)和分维(Fractal dimension)理论应用于植物生态学领域以来，分形理论与地统计学的结合日益紧密，并广泛应用于自然生态和环境学科研究。吴承祯、洪伟等运用分形理论研究杉木种源生长的空间变异规律［2-3］;刘金福等［4］探讨了林分土壤团粒结构的分维特征。目前大部分研究局限于土壤、降水等生态因子及杉木、侧柏、马尾松等少数树种［5-11］，国内对珍稀濒危植物种源生长特性的空间变异研究并不多见。

水松(Glyptostrobus pensilis)，别名水帝松、水杉松等，属杉科水松属，是我国特有的单属种植物，国家一级保护植物。水松作为一种罕见的古生代孑遗树种，在中生代时曾广泛分布于北半球，由于自然地理因素和人为活动的影响，水松数量日益减少，目前仅零星分布于我国南方，处于濒危状态。水松生长于沼泽地，耐水湿，是造船、造桥的优良材料;树根的木质部轻松，浮力大，能做救生工具和木塞;枝叶和果实均可入药;树干粗壮挺直，枝叶疏密适度，既是风景林，又是防风固堤的优良树种。水松在研究杉科植物的系统发育、古植物学和第四纪冰川气候等方面都有重要的科学价值，被世界保护监测中心列为稀有种，中国植物红皮书列为濒危树种，其濒危状况受到国内外许多学者的高度关注。徐英宝［12］对珠江三角洲地区的水松进行了调查;韩丽娟等［13］对水松生物学特性和保护、水松的次生韧皮部解剖及其系统位置进行了分析;徐祥皓等［14］指出水松地理分布的状况;李发根等［15］探讨了水松地理分布和濒危原因;吴则焰、刘金福、郑世群等［16-20］在水松天然种群结构特征及动态规律等方面开展了研究。尽管许多学者从不同角度研究水松，但仅限于形态、生理、生物学等方面，并没能很好地解释水松生态学濒危机制。

笔者在长期开展水松种群生态学研究的基础上，将分形理论与地统计学原理相结合，把水松种源生长空间变异性的复杂程度定量化，探讨水松不同种源胸径、树高生长在空间尺度上的分维变化特征，加深对水松生物学特性的认识，为水松种源的合理区划和种子调拨界限的划定提供坚实的理论基础，对加强珍稀濒危植物水松的保护和种群恢复无疑具有重要意义。

1 试验材料与研究方法

1.1 试验材料

材料选自全国6个省区的14个水松地理种源(表1)，每个种源选取10个20 m×20 m的样地，树高测量采用DQL-6型光学测树罗盘仪，调查每个样地的海拔、坡度、坡向、坡位、土壤条件等因子。采用相邻格子法，将每个样地划分为16块5 m×5 m的小格子样方，对每个样方进行每木检尺，记录样方内所有植株的种名、树高、胸径、冠幅、枝下高(起测径阶≥4 cm)和各树种的调查密度、盖度以及幼苗种类和株数。测定不同种源水松胸径、树高等主要生长性状，计算总平均生长量，进行空间变异性及分形特征研究。

表1 水松不同种源高径平均生长量

1.2 半方差函数

半方差函数是描述树木种源生长特性空间变异结构的函数。进行半方差分析时，必须以内蕴假设(Intrinsic hypothesis)为前提，即假设某区域化变量Z(x)的均值稳定，方差存在且为有限，该值仅与间距有关，则半方差函数可定义为区域化变量增量的方差［21］。

其一般表达式为：

由于 r(h)=var［Z(x)-Z(x+h)］/2，故称 r(h)为该参数间距为h的半方差函数，计算公式为：

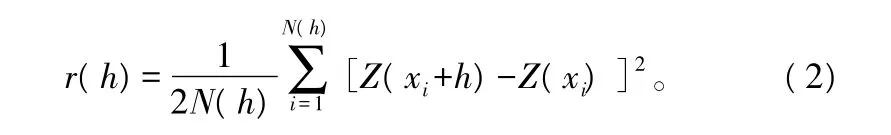
式中：h为样本间距，又称滞后距;N(h)为间距为h的样本对数。

1.3 分形维数

分形维数是描述分形体自相似特征的主要工具，即对分形体的有效表征。自然界各种现象中，如地震、水流、气候等都有此特征，表面看似无序，实际却存在规律性。尽管分形对象复杂，但仍可找到不变测度，即分形维数(简称分维)。分维值(D)的大小是事物复杂程度的一种量度。由于树种种源是一个不均匀的复合体，与气候、水文、地形、地质等诸多因素相互作用，导致树种种源生长特性参数值在空间表现为很不规则，呈随机性，适合用分维布朗运动来量度。

用布朗运动来近似表示树种种源生长特性变异，其一维半方差函数定义为

式中：Z(x)、Z(x+h)分别为x、x+h处树种种源生长特性测定值;h为间距;H为幂指数。

对于布朗运动，幂指数H等于0.5;对于树种种源生长特性空间变异，H的取值范围为0～1.0，随着H的增加，其空间变异性逐渐增强，其分形维数由公式D=2-H给出。

由式(2)，改变一对数据的间距，得到对应的半方差值，把半方差和间距绘到双对数坐标纸上。对于分形曲线，log r(h)与log h存在线性关系，用最小二乘法进行线性回归，得到回归直线的斜率m。分形维数D可用D=(4-m)/2进行计算。

分形值(D)表征树种种源之间的结构性，D值越大，说明树种种源之间生长特性值的差异越小，即均一性程度越好;D值越小，说明树种种源之间生长特性值的差异越大，即均一性程度越差，适宜作为种源选择的指标。

2 结果与分析

2.1 水松种源生长特性的传统统计值

按照经典的方法，水松种源生长特性的传统统计特征值分别为：胸径均值为36.22 cm，树高均值为15.94 m，不同种源水松胸径、树高变化范围为31.7～40.1 cm 和 12.7～17.6 m，变异系数分别为0.071 7 和0.094 6，方差分别为6.752 6 和2.276 5，标准差分别为2.598 6和1.508 8。因此，传统统计值只能在一定程度上反映样本总体，不能定量刻画种源生长特性的随机性和不规则性、独立性与相关性。要解释并进行定量化，必须进一步对空间变异结构进行分析。

2.2 水松种源生长特性的分形维数

在一个连续的分布区，若树种种源生长特性变量随距离增加呈单调变化，则该变量具有严格的空间依赖性，对应的分维值D等于1;若某变量的值不可预知，则该变量在空间上是完全独立的，其对应的分维值D等于2。大部分树种种源生长特性值介于上述两种情况之间，即对应的分维值D介于1～2之间。

在地统计学中，半方差图集中体现了作为尺度函数的变量与尺度之间的依赖变化情况。若两相邻种源与两个远距离种源的实际测值没有差别，在不同尺度上的半方差r(h)也就没有差别，其半方差图将是水平的，对应的分维值D等于2，表明该变量在连续尺度上是空间独立的;若半方差图是线性的，说明该变量具有统计自相似，即大尺度格局是小尺度格局的放大形式。分维值D不随尺度的变化而变化，即D是尺度的常数函数，说明变量是空间依赖的。

由式(2)得到一组log r(h)与log h值，用最小二乘法进行线性回归，得到回归直线的斜率m，由式(4)算出水松种源胸径、树高生长特性值的分形维数D(表2)。

表2 水松种源胸径、树高生长特性的分维值

由表2可知，水松种源胸径、树高生长的分维值分别为1.635与1.824，相对应的幂指数H范围为0～0.5，表明随着间距的增加，胸径、树高生长各自的半方差之间是负相关，即将胸径、树高的半方差标准正态化后，这些值的半方差有正、负值，并非单一的正值或负值。D值越大，表明短距离的变异影响占主导地位。

D值表示树种种源生长特性值在空间的不均一程度。D值越大，对应的生长特性值分布均一性越好。水松种源胸径生长特性的分维值低于树高生长特性的分维值，可见水松种源胸径生长空间变异性大于树高生长空间变异性。因此，胸径生长指标更能切实反映水松种源的空间差异性，应作为水松种源优劣评价的主要指标。水松种源采种间距应根据其胸径分维值的大小而调整，以充分利用其空间变异性。

2.3 自相关检验

水松种源胸径、树高生长特性的分维值测算是否有效，可运用log r(h)与log h回归方程的自相关检验进行验证。经计算，水松种源胸径、树高生长特性的log r(h)与log h回归方程自相关检验统计量d依次为0.901 2和1.982 3，大于杜宾-华生检验表的临界值du(du为上临界值)。因此，接受自相关不显著的假设，即水松种源生长特性值log r(h)与log h之回归关系各期误差间不存在线性自相关，说明求解得到的log r(h)与log h之间的线性斜率是有效的。可见，据此测算出的分维值确实反映了胸径、树高生长的空间变异性，从而为水松种源试验的采种布点及评价指标确定提供了理论依据。

3 结论与讨论

分形维数能够真实反映树木生长的实际情况，体现了树木生长特性在空间的不均一程度。分维值较大，其样本间的均一程度较好;分维值较小，分布均匀性变差。研究结果表明，水松种源树高与胸径存在分形特征，满足自相似规律。水松种源胸径、树高生长特性的分维值分别为1.635和1.824，胸径的分维值小于树高的分维值。为反映水松种源的空间差异性，在评价水松种源时应选取胸径生长指标。由于野外调查存在的数据误差难以避免，尤其是树高和胸径的误差可能影响研究结果，但该结论基本反映了水松种源高径生长的空间变异规律。应用分形理论与地统计学原理相结合的方法分析水松种源的胸径、树高生长的空间变异性及其分形特征，可以为水松种源合理区划和保护提供理论依据。水松种群濒危机制有待进一步深入探讨。

［1］洪伟，吴承祯.杉木种源胸径生长地理变异规律的研究［J］.植物生态学报，1998，22(2)：186-192.

［2］吴承祯，洪伟.杉木数量经营学引论［M］.北京：中国林业出版社，2000：100-114.

［3］洪伟，吴承祯.杉木种源高径生长的空间变异及其分形特征［J］.福建林学院学报，2001，21(2)：97-100.

［4］刘金福，洪伟，吴承祯.中亚热带几种珍贵树种林分土壤团粒结构的分维特征［J］.生态学报，2002，22(2)：197-205.

［5］苏里坦，宋郁东，张展羽.天山北麓地下水与自然植被的空间变异及其分形特征［J］.山地学报，2005，23(1)：14-20.

［6］杨传强，丰震，孙仲序，等.21年生侧柏种源的地理变异及种源选择［J］.山东农业大学学报：自然科学版，2005，36(2)：196-198.

［7］徐冰，陈亚新，郭克贞.半干旱草地土壤粒径分形维数及空间变异特征［J］.水利学报，2007(S1)：691-673.

［8］贾晓红，李新荣，张景光，等.沙冬青灌丛地的土壤颗粒大小分形维数空间变异性分析［J］.生态学报，2006，26(9)：2827-2833.

［9］Wang K，Zhang R D，Wang F Q.Testing the pore solid fractal model for the soil water retention function［J］.Soil Science Society of America，2005，69：776-782.

［10］马克明，祖元刚.兴安落叶松分枝格局的分形特征［J］.植物研究，2000，20(2)：235-241.

［11］孙博玲.分形维数(Fractal dimension)及其测量方法［J］.东北林业大学学报，2004，32(3)：116-119.

［12］徐英宝，余醒.珠江三角洲的水松生长调查［J］.华南农学院学报，1980，1(4)：107-110.

［13］韩丽娟，胡玉熹.水松生物学特性及保护(综述)［J］.亚热带植物通讯，1997，26(1)：43-47.

［14］徐祥皓，黎敏萍.水松的生态及地理分布［J］.华南师范大学学报，1959，4(3)：84-99.

［15］李发根，夏念和.水松地理分布及其濒危原因［J］.热带亚热带植物学报，2004，12(1)：13-20.

［16］吴则焰，刘金福，洪伟，等.水松自然种群和人工种群遗传多样性比较［J］.应用生态学报，2011，22(4)：873-879.

［17］吴则焰，刘金福，洪伟，等.孑遗植物水松(Glyptostrobus pensilis)种群优势度增长规律研究［J］.武汉植物学研究，2009，27(4)：387-390.

［18］吴则焰，刘金福，洪伟，等.孑遗植物水松(Glyptostrobus pensilis)数量性状间的相关聚类分析［J］.北华大学学报：自然科学版，2009，10(4)：358-361.

［19］刘金福，洪伟，吴则焰，等.孑遗植物水松(Glyptostrobus pensilis)种群生命表和谱分析［J］.武汉植物学研究，2008，26(3)：259-263.

［20］郑世群，刘金福，吴则焰，等.屏南水松天然林主要种群的种间竞争［J］.福建林学院学报，2008，28(3)：216-219.

［21］吴承祯，洪伟.杉木种子涩籽的空间变异性研究［J］.应用与环境生物学报，1998，6(1)：15-19.