基于独立分量分析的实正交空时分组码盲识别

赵知劲，陈林，王海泉，沈雷

(1. 杭州电子科技大学 通信工程学院，浙江 杭州 310018；2. 中国电子科技集团第36研究所 通信系统信息控制技术国家级重点实验室，浙江 嘉兴 314001)

1 引言

通信信号识别在民用通信和军用通信中具有重要意义。传统通信信号识别主要包括调制识别和信道编码识别。在非合作的通信侦察中，要想截获信号信息，必须知道调制方式、信道编码方式和编码参数等。空时码[1]是对MIMO系统中发送符号的一种编码，空时码的识别是非合作MIMO系统的重要内容之一，已引起国内外学者的关注。

2007年，Shi M、BAR-NESS Y等人[2]提出的区分空时码（STC）和分层空时码（BLAST）的方法。利用STC和BLAST这两者在信号相关性上的差异，提出了利用循环平稳特性区分2种编码的方法。2008年，YOUNG M D、HEALTH R等人[3]在只有一根接收天线的条件下，利用Alamouti码的四阶循环累积特性，用来区分Alamouti码与一般的空间复用方案。2008年，Vincent Choqueuse等人[4,5]提出利用相关矩阵的空时分组码（STBC）识别方法。该方法根据不同空时分组码的相关矩阵在不同时滞下的 Frobenius范数是否为零的差异性，首先计算接收信号的相关矩阵 Frobenius范数，然后采用决策树分类器，最后实现对空时分组码的识别。2010年，Vincent Choqueuse和Mélanie Marazin等人[6]提出基于最大似然识别的3种STBC分类器：最优分类器、二阶统计量（SOS, second-order statistic）分类器、码参数（CP, code parameter）分类器，实现了对空时分组码的识别，其中码参数分类器能够实现盲识别。文献[4～6]所提方法能够识别具有不同码率或码长的空时分组码，但没有进一步研究空时分组码类型的识别。

然而，要对接收信号进行解码，需要知道它的编码方式，目前还没有公开报道这方面的研究，因此需要进一步识别空时分组码的类型。

针对此问题，本文首先建模得到与虚拟信道矩阵相关的接收信号模型，由于虚拟信道矩阵包含空时码信息，因此可用于空时码识别；然后利用ICA算法盲估计出虚拟信道矩阵，计算得到虚拟信道矩阵的相关矩阵；再者根据实正交空时分组码的特性，提出相关矩阵的稀疏度和方差的识别特征参数；最后提出利用此参数的正交空时分组码识别方法。

2 信号模型

考虑传统的具有Tn个发射天线和Rn个接收天线的实正交空时分组码系统。在发射之前对信号进行分组，N个符号通过 L个时隙发射，令为待发射的由N个符号组成的第 k组数据，且其中各符号独立分布。S ( k )先经过空时调制映射为一个具有 L个时隙的nT×L维空时编码矩阵C(k)[7]，C(k)可表达成如下形式

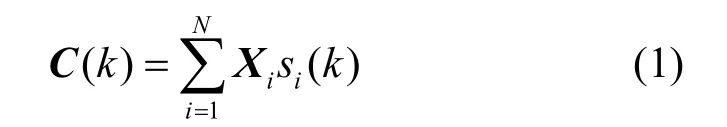
其中， Xi为第i个符号 si( k)的nT×L维编码矩阵，并具有下列性质[8]：

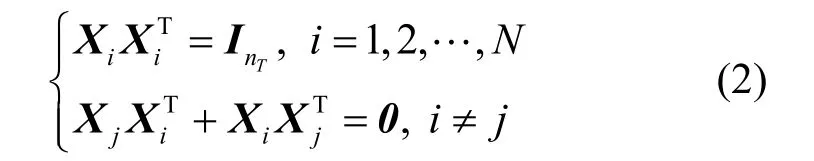
其中， InT是一个 nT×nT的单位矩阵。

第k组的接收数据信号 Y ( k)可以表示为

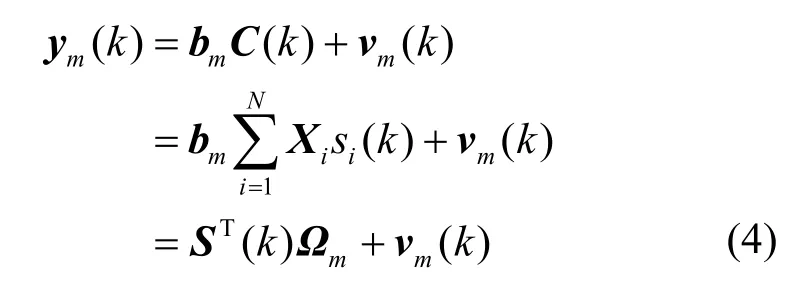
转置式（4）可得

式（6）可表示为

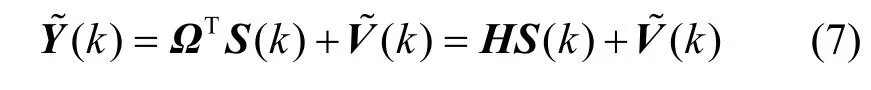
3 特征提取与识别方法

3.1 虚拟信道矩阵的特点

分析虚拟信道矩阵的相关矩阵，令A = HTH = ΩΩT可得

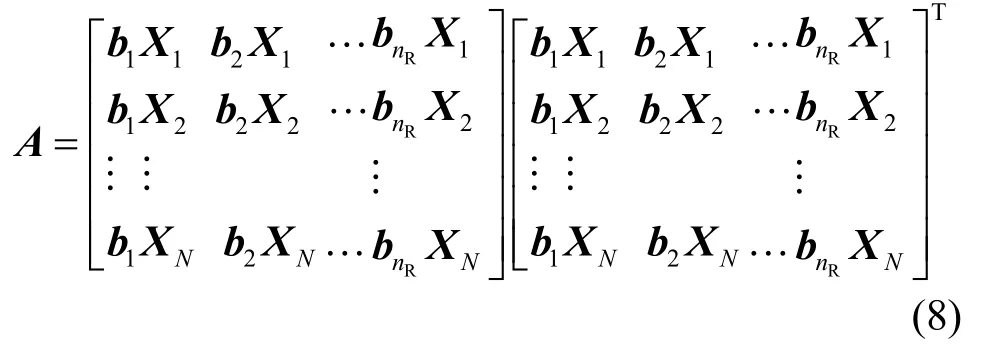
对正交空时分组码，A的第(i, i)元素为

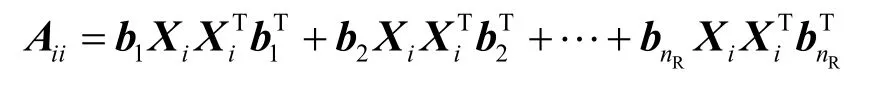
利用式(2)可得

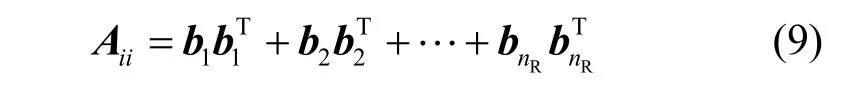
A的第(i, j)元素为

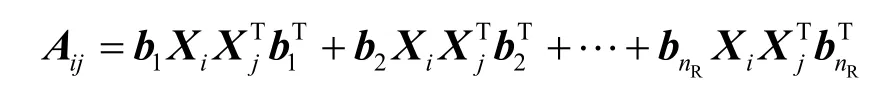
因为ijA是一个标量，则利用式（2）可得

因此，当ij≠时，

根据式（9）、式（10）可知

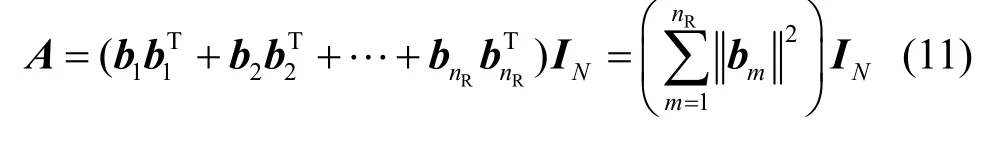
所以正交空时分组码的A是一个NN×维的对角矩阵。

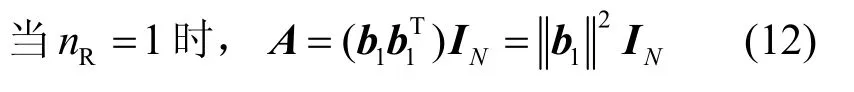
如果不是正交空时分组码，则式（2）不成立，于是A也不是对角矩阵，即式（11）不成立。

3.2 特征参数选取

根据矩阵A的这种特性，提出矩阵A的稀疏度的特征参数θ，即θ表示A中非零的个数。

由于消噪参数 γ的选择直接影响特征参数θ值。如果是正交空时分组码，应取较大的消噪参数γ=γ1，才会使θ=N并有较高识别率；如果是非正交空时分组码，应取较小的消噪参数 γ =γ2，才会使θ＞N并具有较高识别率。

由于正交空时分组码的A是一个2N×2N维的对角矩阵，理论上应有非主对角元素方差 D = 0 ，但实际中由于A矩阵估计误差，D不会严格为零。非正交空时分组码的A矩阵是非主对角矩阵，所以D＞ 0 。为了解决消噪参数 γ的选择问题，利用正交空时分组码和非正交空时分组码的矩阵非主对角元素具有不同分散程度的特点，本文提出矩阵的非主对角元素方差D作为另一个特征参数，来预判码型，确定参数γ值，设方差判决门限为 DT。

3.3 识别方法

由于 A = HTH，关键是要得到H。由式（7）可知，(k)是一个瞬时混合信号模型，得到(k)后，采用FASTICA算法[9,10]就可以估计出，然后就可估计出矩阵。

所以本文提出的基于 ICA的利用非对角元素方差和稀疏度的实正交空时分组码的盲识别方法（简记为DS-ICA）步骤如下。

3) 计算矩阵 nR= 2 特征参数D，预判码型，选取对应的γ。

6) 当θ=N时，则判为正交空时分组码；当θ＞ N 时，则判为非正交空时分组码。N为判决门限，它是每个分组的符号数。

仅利用非对角元素方差的正交空时分组码的盲识别方法（简记为D-ICA）的步骤为：步骤1)、步骤2)、步骤3)，预判码型即为最终判决结果。

4 算法仿真和分析

仿真中参数选择如下：发射信号 si( k)是BPSK调制的星座符号，则 si( k)∈{-1 ,1}，发射数据为1 000组，L=N=4，信道为准静态稳定信道。

1) 估计误差分析。发射天线数 nT= 4 ，接收天线数 nR= 1 和 nR= 2 时，正交空时分组码非正交空时分组码在无噪声和信噪比为5dB时估计得到正交空时分组码和非正交空时分组码的矩阵分别如表1和表2所示。

2) 消噪参数γ的选取。

在信噪比 SNR=0dB、不同发射天线数 nT和接收天线数消噪参数(t = 5 ,6,… ,3 0)情况下，正交空时分组码和非正交空时分组码特征参数θ如图 1所示，消噪参数γ与正交空时分组码正确识别概率 POD和非正交空时分组码正确识别概率 PND的关系曲线如图2和图3所示，图中曲线是1 500次仿真结果的平均。

由于随着参数t增大，即参数γ变小，B就不易是对角矩阵，因此 POD将变小，而 PND将增大。由图可见，当t=5时， POD接近100%，因而取当t=30时， PND具有较大值，因而取

表1 无噪声时矩阵

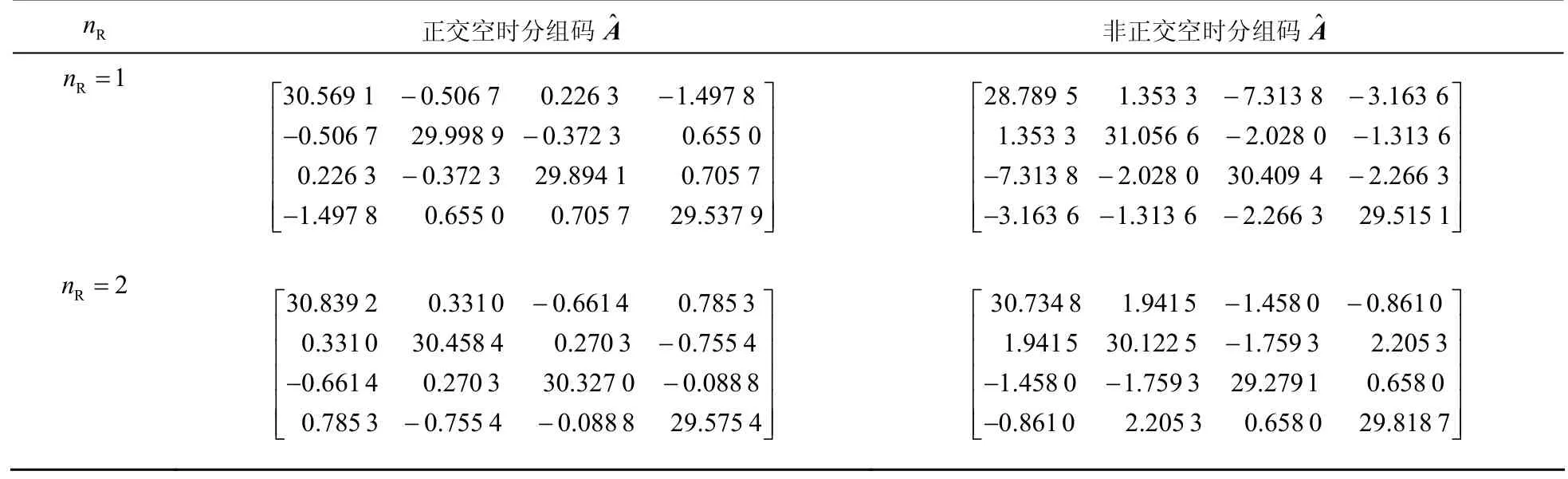
表1 无噪声时矩阵

R n 正交空时分组码ˆA 非正交空时分组码ˆAR1n= 30.569 1 0.506 7 0.226 3 1.497 8 0.506 7 29.998 9 0.372 3 0.655 0 0.226 3 0.372 3 29.894 1 0.705 7 1.497 8 0.655 0 0.705 7 29.537 9--■■■■-■-■ -■-■■■■■28.789 5 1.353 3 7.313 8 3.163 6 1.353 3 31.056 6 2.028 0 1.313 6 7.313 8 2.028 0 30.409 4 2.266 3 3.163 6 1.313 6 2.266 3 29.515 1- -■■■■- -■■■■- - -■■- - -■■R2n= 30.839 2 0.3310 0.6614 0.7853 0.3310 30.458 4 0.2703 0.755 4 0.6614 0.2703 30.327 0 0.0888 0.7853 0.755 4 0.0888 29.575 4-■■■■-■■■■--■■- -■■30.7348 1.9415 1.4580 0.8610 1.9415 30.1225 1.7593 2.2053 1.4580 1.7593 29.2791 0.6580 0.8610 2.2053 0.6580 29.8187- -■■■■-■■■■- -■■■-■

表2 SNR=5dB时矩阵

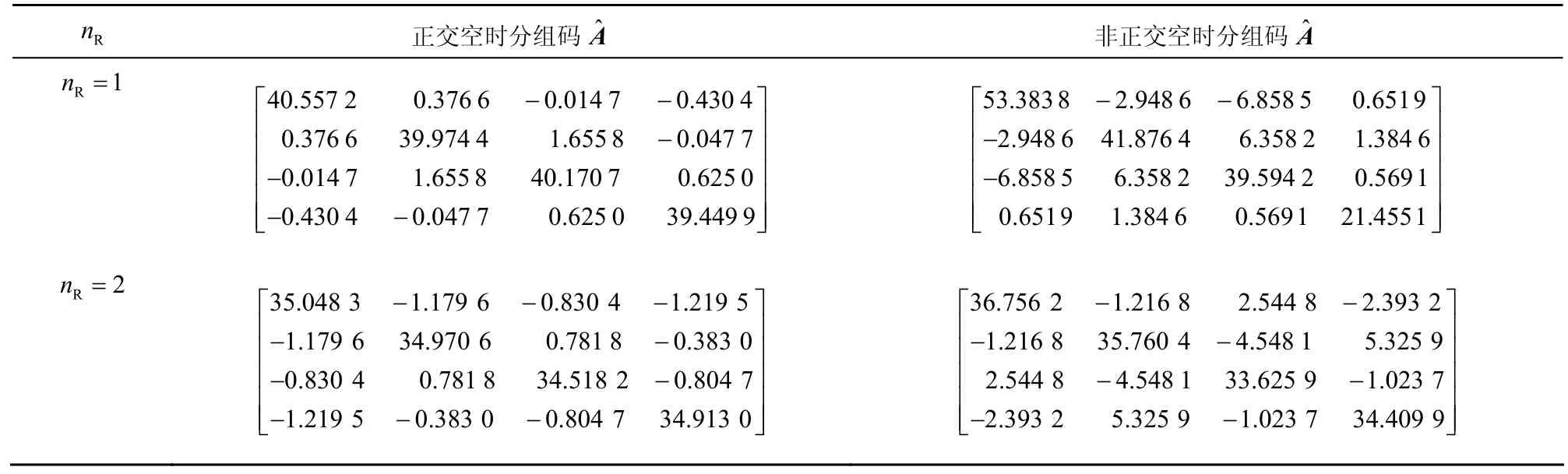
表2 SNR=5dB时矩阵

R n 正交空时分组码ˆA 非正交空时分组码ˆAR1n= 40.557 2 0.3766 0.014 7 0.430 4 0.376 6 39.974 4 1.6558 0.047 7 0.014 7 1.6558 40.170 7 0.6250 0.430 4 0.047 7 0.6250 39.4499- -■■■■-■■■■-■■- -■■53.3838 2.9486 6.8585 0.6519 2.9486 41.876 4 6.3582 1.384 6 6.8585 6.358 2 39.594 2 0.5691 0.6519 1.384 6 0.5691 21.4551- -■■■■■-■■■-■■■■R2n= 35.048 3 1.179 6 0.830 4 1.219 5 1.179 6 34.970 6 0.781 8 0.383 0 0.830 4 0.781 8 34.518 2 0.804 7 1.219 5 0.383 0 0.804 7 34.913 0- - -■■■■-■-■■■--■■- - -■■■36.756 2 1.216 8 2.544 8 2.393 2 1.216 8 35.760 4 4.548 1 5.325 9 2.544 8 4.548 1 33.625 9 1.023 7 2.393 2 5.325 9 1.023 7 34.409 9--■■■-■-■■■--■■-■-■

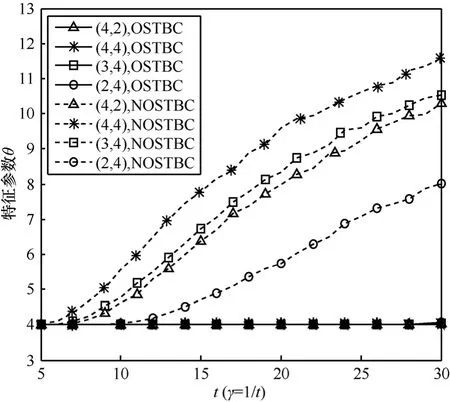
图1 不同γ时特征参数θ的变化

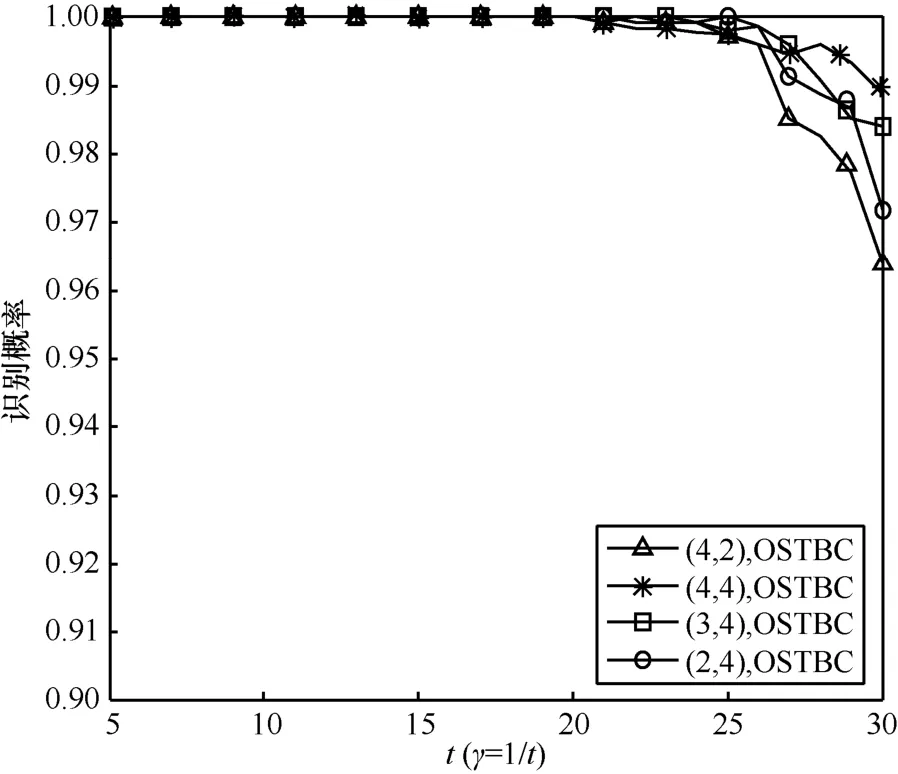
图2 正交空时分组码正确识别概率与γ关系

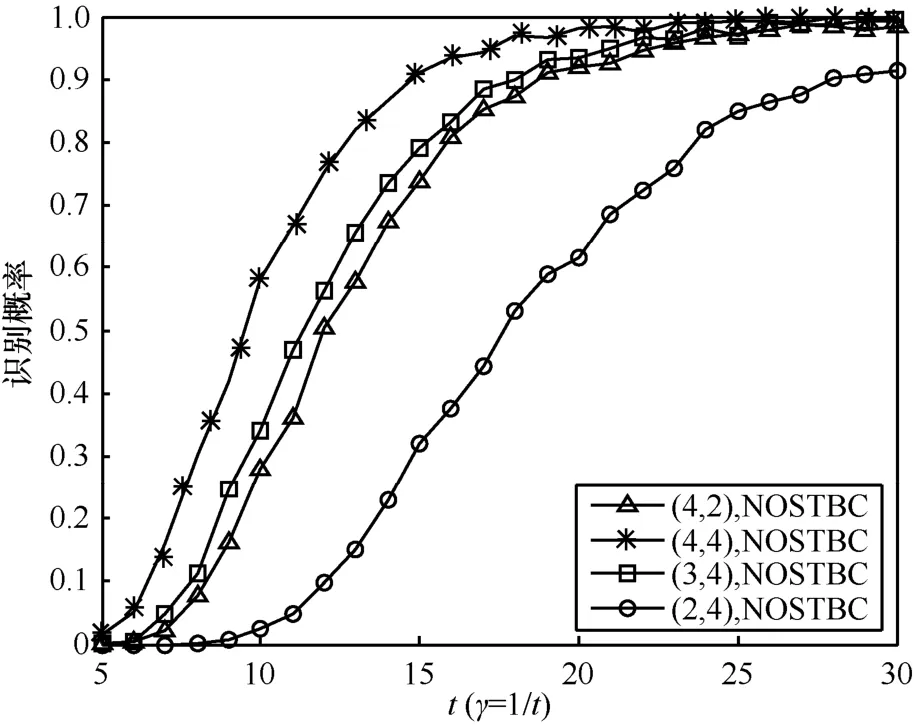
图3 非正交空时分组码正确识别概率与γ关系

在不同信噪比、不同 ( nT, nR)下，正交空时分组码时取非正交空时分组码时取1 500次实验结果的特征参数θ的平均值如图4所示。由图4可见，正交空时分组码的θ=4保持不变；非正交空时分组码的θ取值在6～13之间。正交空时分组码和非正交空时分组码的曲线没有交叉，区分性好。

由图1～图4可见，收发天线中有一个减少，非正交空时分组码的特征参数θ值就减小，正确识别概率就降低。不同信噪比、不同 ( nT, nR)下，特定γ时正交空时分组码的特征参数θ和正确识别概率基本不变。

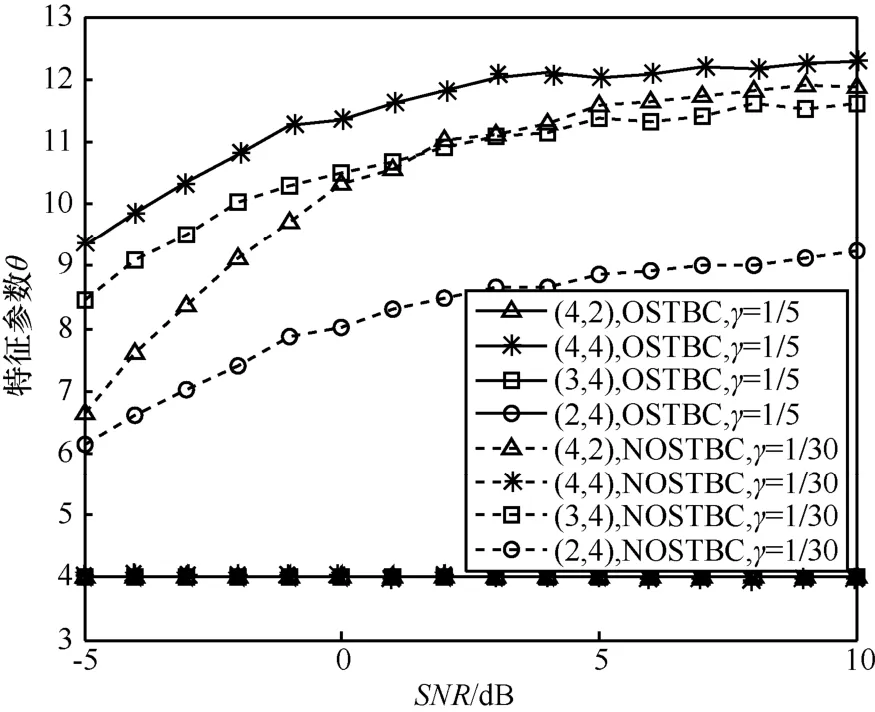
图4 特定γ时特征参数θ的变化

3) 非主对角元素分散度分析。不同信噪比、不同 ( nT, nR)时正交空时分组码和非正交空时分组码的特征参数D的200次仿真结果的平均值如图5所示。由图5可知，信噪比在-5dB和10dB之间时，非正交空时分组码的D大于正交空时分组码的D，两者基本不重叠；随着 SNR变化，正交空时分组码的D值基本不变，而非正交空时分组码的D值略有变化；当接收天线数和发射天线数中任何一个值增大，非正交空时分组码的D值将增大，而正交空时分组码的D值增加很小。

4) 正确识别概率分析。根据上述仿真结果，取方差判决门限 DT= 0 .8。当 D＞DT时，取在不同信噪比、不同 ( nT, nR)下，本文所提出的DS-ICA法对正交空时分组码和非正交空时分组码的正确识别概率曲线和错误识别概率曲线如图 6和图 7所示，图中曲线是1 500次仿真的平均。

由图6可知，当 S NR≥ 6 dB 时，DS-ICA法对正交空时分组码的正确识别概率基本达到 100%，不同收发天线数，DS-ICA法对正交空时分组码的识别影响较小。由图7可知，在收发天线数为（3，4）和（4，4）时，当 S NR≥ 3 dB 时，DS-ICA法对非正交空时分组码的正确识别概率达到98%以上；当接收天线数和发射天线数中任何一个值增大，DS-ICA法对非正交空时分组码的正确识别概率将增大；当收发天线数为（2，4）和（4，2）时，当信噪比大于0dB以后，再增大信噪比，DS-ICA法对非正交空时分组码的正确识别概率提高缓慢，对非正交空时分组码的识别性能有待进一步提高。

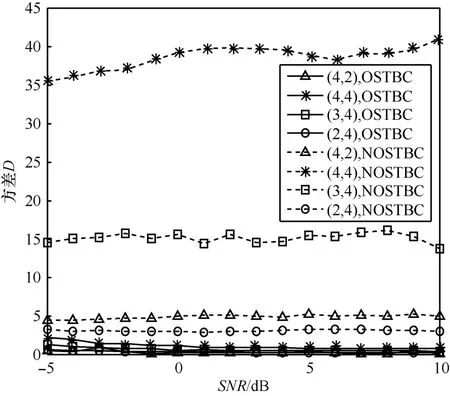
图5 特征参数D的变化

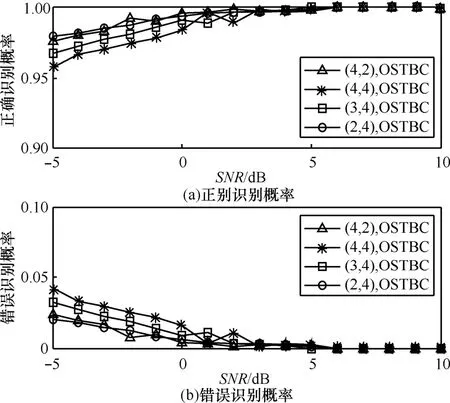
图6 正交空时分组码正确识别概率与错误识别概率

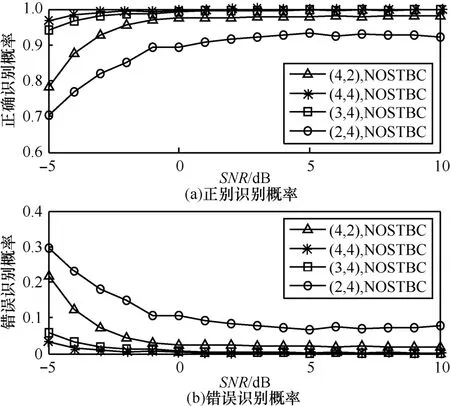
图7 非正交空时分组码正确识别概率与错误识别概率

为了说明本文方法的有效性，与文献[4]方法进行性能比较。给定以下 2种码[4]： ( nT, nR)取值为(2,4)时的正交空时分组码：和(nT, nR)取值为(3,4)时的正交空时分组码：不同信噪比下，利用文献[4]的方法、本文提出的D-ICA法和DS-ICA法分别对上述2种正交空时分组码的正确识别概率曲线如图8所示，图中曲线是1 500次仿真的平均。

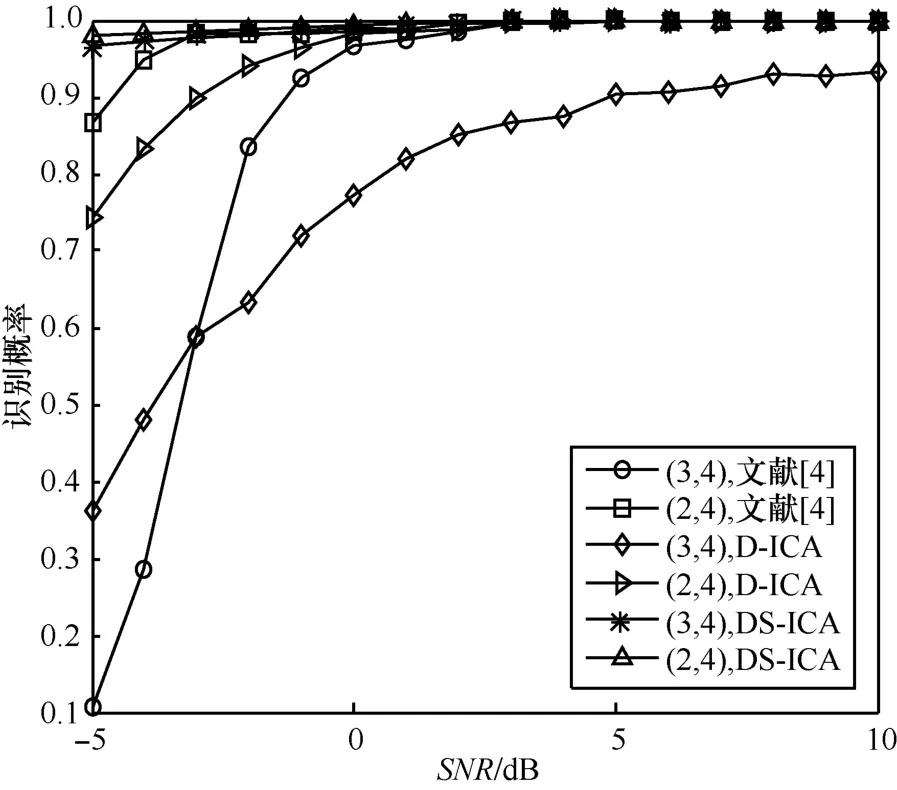
图8 2种正交空时分组码正确识别概率

由图8可知，( nT, nR)值为(2,4)，当 S NR＞2dB时，3种方法的正交空时分组码正确识别概率都基本达到100%；当 S NR≤ 2 dB 时，DS-ICA法最好，文献[4]方法次之，D-ICA法最差。当 ( nT,nR)值为(3,4)，DS-ICA法最优；低信噪比（ S NR≤-3dB ）时，D-ICA法对正交空时分组码的正确识别概率比文献[4]方法高；当 S NR＞-3 dB 时，文献[4]方法对正交空时分组码的正确识别概率比D-ICA法高。

综上所述可得，本文提出的DS-ICA法识别性能最好，文献[4]方法次之，D-ICA法最差。

5 结束语

本文利用正交空时分组码特性提出了一种正交空时分组码盲识别方法。首先利用ICA算法盲估计出虚拟信道矩阵，然后计算虚拟信道矩阵相关矩阵的2个特征参数：稀疏度和方差，最后利用门限进行判决。仿真结果表明：收发天线数对DS-ICA法的正交空时分组码识别影响较小，当SNR≥ 6 dB 时，正交空时分组码的正确识别概率基本达到100%；非正交空时分组码的识别性能与收发天线数有关，当收发天线数为（3，4）和（4，4）且 S NR≥ 3 dB 时，对非正交空时分组码的正确识别概率达到98%以上。利用本文所提出的2个特征参数可以有效地区别正交空时分组码和非正交空时分组码。本文仅讨论了实正交空时分组码，复正交空时分组码的盲识别有待进一步研究。

[1] 王海泉, 陈颖, 赵知劲. 多天线系统中的空时码技术[M]. 北京: 科学出版社, 2011.WANG H Q, CHEN Y, ZHAO Z J. Space-time Codes Technology for Multiple Antennas System[M]. Beijing: Science Press, 2011.

[2] SHI M, BAR-NESS Y, SU W. STC and BLAST MIMO modulation recognition[A]. IEEE Global Telecommunications Conference[C].Washington, DC, USA, 2007.3034-3039.

[3] YOUNG M D, HEALTH R, EVANS B L. Using higher order cyclostationarity to identify space-time block codes[A]. IEEE Global Telecommunications Conference[C]. New Orleans, Louisiana, USA,2008.3370-3374.

[4] CHOQUEUSE V, YAO K, COLLIN L, et al. Hierarchical space-time block code recognition using correlation matrices[J]. IEEE Trans on Wireless Communications, 2008, 7(9):3526-3534.

[5] CHOQUEUSE V, YAO K, COLLIN L, et al. Blind recognition of linear space time block codes[A]. ICASSP’2008[C]. Las Vegas, Nevada, USA, 2008.2833-2836.

[6] CHOQUEUSE V, YAO K, COLLIN L, et al. Blind recognition of linear space time block codes: a likelihood-based approach[J]. IEEE Trans on Signal Processing, 2010,58(3): 1290-1299.

[7] LIU J, ISERTE A P, LANGNAS M A. Blind separation of OSTBC signals using ICA neural networks[A]. IEEE International Symposium on Signal Processing and Information Technology[C]. Darmstadt,Germany, 2003.502-505.

[8] JAFARKHANI H. Space Time Coding: Theory and Practice[M].Cambridge: Cambridge University Press, 2005.

[9] HYVARINEN A, OJA E. Independent component analysis algorithms and application[J]. Neural Networks, 2000, 13(415): 411-430.

[10] HYVARINEN A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Transactions on Neural Networks, 1999, 10(3): 626-634.