面向可重构基础网络的部分扇出多播交换阻塞率模型
2012-08-04张博汪斌强朱圣平
张博,汪斌强,朱圣平
(国家数字交换系统工程技术研究中心,河南 郑州 450002)
1 引言
目前,互联网开始进入下一代网络新时期,据2010年Arbor公司与美国密西根大学的一份持续2年的联合研究报告[1],多媒体音视频的应用服务成为了当今互联网的发展主流。中国互联网络信息中心(CNNIC)2011年7月中国互联网络发展状况统计报告[2]表明:网络视频继续保持平稳增长,2011年6月中国网络视频用户达3.01亿,作为与线下电视最为相近的互联网服务,网络视频服务是使用最多的服务之一。视频流有典型的特性,其数据内容趋向于单点发送,多点接收,即多播。如今流行的基于视频应用的 IPTV、视频会议、交互式仿真、多方游戏等应用的流量都具有多播特性。
多播交换结构研究开始于 1984年,Huang和Knauer首次对ATM网络中多播数据的交换问题予以关注,并设计一种新型交换结构来支持多播,由此提出了第一个多播交换结构——Starlite[3]。1988年,Deering[4]提出了将多播功能结合到数据网 IP层的多播结构。1992年,多播实验网——Mbone建立[5]。目前,较完整的多播协议体系已经形成,IP多播的研究工作逐渐集中于流量控制和拥塞控制研究,无线多播研究和大规模高效多播研究。
对于大规模高效多播研究,基于banyan的多播交换结构大多采用多播复制的方法,Tony Lee[6]提出了一种内部无阻塞的复制网络设计方案,但结构过于复杂。文献[7]对该结构进行改进,但输入分组复制要求的总和超出输出端口的数量时,满溢的现象便会发生。Yeh等人[8]提出了一种基于Knockout理论多播交换结构,每个输入端口采用完全连接的方式连接到所有的输出接口模块。但该方案的大规模扩展性能存在瓶颈。基于Clos结构的多播交换,文献[9]引入了一种路径分配向量,但整个路径决策时间复杂度为O(K),无法大规模扩展。2010年的文献[10]证明了对Clos网络进行多播路径匹配是NP完全问题。基于Crossbar多播交换结构是当前的主流类型,Pan等人[11]提出了一种将信元载荷与目的地址信息分开存储的方案,但交换结构的加速比高。文献[12]针对IPTV提出了一种扇出无关的多播交换结构,但该结构要求到达过程满足强大数定律,且多播输出阻塞率高。基于Crossbar缓存单多播联合调度算法[13]采用了分级和层次化的调度机制,但该调度机制仍然存在O(N( 2N- 1 ))队列复杂度瓶颈。
以上分析中多播结构和调度机制固有的瓶颈使其不具备大规模扩展能力,可重构信息通信基础网络理论体系[14]对多播问题的原因进行了分析。从多播研究的整体看,终端基本是以软件方式实现各种应用层,通常不存在瓶颈,而路由交换节点的实现是多播性能的关键。路由交换节点的多播实现方式可以分为多次单播软件调度方式和硬件电路线速扇出拷贝方式。目前路由交换节点上多播多数采用多次单播的软多播[15],即在路由前对多播分组先进行复制而后各自在源端口队列排队,但软多播实时性差,不能保证服务质量。
在可重构基础网络中,有效弥合多播业务特性和网络服务能力的一个途径是将多播业务特征需求与网络承载服务二者抽象成一种特定的“业务—服务”映射模型,多播服务根据多播业务需求,构建节点和链路资源独享的可重构多播服务承载网,这就要求交换层面必须采用完全分布式的控制机制,才能将节点交换资源有效分割给多播业务。因此,可重构基础网络多播交换机制采用硬件电路线速扇出的多播拷贝方式和自路由寻路方式。其分布式自路由寻路方式有效地解决了缓存调度的瓶颈问题;其线速扇出与网络负载相适应,避免了输出竞争等待;其等级数的交换路径,时延抖动小,避免了时延抖动大造成的多播性能下降问题。
基于此,本文提出了部分扇出多播交换阻塞率模型,该模型具有完全分布式自路由,无需端口匹配,无内部缓存,无缓存时延的特点。当构建纯多播服务承载网或单多播混合服务承载网时,可采用关闭部分22×布尔单元和级间比特置换的重构操作实现其交换资源的逻辑隔离,由于其分布式的特点,多播服务承载网之间无相关性,大大简化了多个可重构服务承载网构建的控制复杂度,增强了多播交换结构的可扩展性。
2 逐级部分扇出交换结构
定义1[16]并播单元:0-1并播单元输入定义在字母表{0 -bound, 1 -bound,idle,bicast} ,即定义在{10,11,00,bicast}域中,规定10 < 00 =bicast<00,bicast为一个输入端的输入信号同时输出到Output-0和 Output-1,在判决选路时,使用表 1的规则。当bicast与空为输入时,则输出端口同时输出该信号。
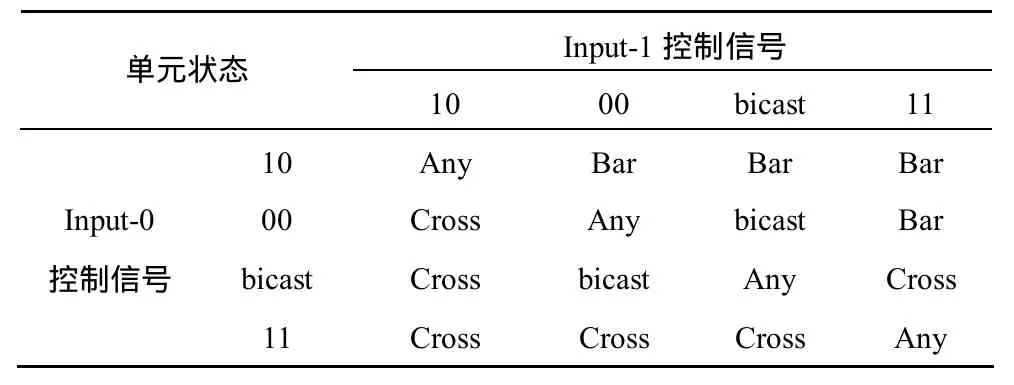
表1 基于{10,bicast,11}域的输入控制
定义2[16]布尔单元:0-1并播单元可以看成22×的布尔单元,其交换规则为:输入为含有2个元u和v的偏序集,输出相当于对输入偏序集中的元求上确界和下确界,由格理论知u∧v为下确界,u∨v为上确界。
其中,u∨v=uorv,u∧v=uandv,如图1所示,满足:当u≤v时,则u∧v=u,u∨v=v,当u≥v时,则u∧v=v,u∨v=u。

图1 布尔单元
0,1,I,B分别代表0 -bound, 1 -bound,idle,bicast输 入 , 则 有 表 达 式0 ∧ 1 = 0 ,0 ∨ 1= 1 ,I∧B= 0 ,I∨B=1。
定义3 布尔群组集线器:采用布尔单元组成的banyan类网络或扩展banyan类网络为布尔群组集线器,对于2G- t o-G的布尔群组集线器满足:该集线器将2G个输入信号中最大的G个信号传输到具有最大输出地址(输出端口从上往下的地址编序为二进制表示的0→2G-1)的G个输出端口,并将其余信号传输到最小输出地址的G个输出端口。
2G- t o-G布尔群组集线器构建方法可参见文献[17],以双调循环排序器为例,其基本排序原理如图2所示,采用点线式表示双调循环排序器网络,设a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p∈P,P为线性序集,根据布尔多项式比较方式可以得到排序序列A1≤A2≤ … ≤A16,其中,A1=a∧b∧ …∧p,A16=a∨b∨ … ∨p。如果P是{0,1},则a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p中任意输入为 1通过该网络都可以到达输出端的8个高地址,其余的到达8个低地址,假设该输入中有6个输入变量为1,即a= 1 ,f= 1 ,g= 1 ,k= 1 ,m= 1 ,o=1,经该集线器,得到A11=A12=A13=A14=A15=A16=1.
对于一个N×N的单播交换结构,其输入信元目的地址可能组合为NN。而对于N×N多播交换结构,由于每一个输入信元的目的地址可能是部分或全部输出端口的组合,则整个交换结构其输入信元目的地址的组合多达(2N- 1 )N。当N大时,大规模多播交换结构的调度配对具有很高的复杂性,因此在大规模(如万端口交换结构)的情况下,要求交换结构在数据传输控制过程中不能采用集中式方式,而要分布式配对,以减小复杂度,因此采用自路由的方式来实现多播数据传输。由于一个多播信元有2N- 1种目的地址的组合,其信元分组自路由的编码开销的最少二进制位为O(lb(2N- 1 )) ≈O(l b 2N) =O(N),当交换结构的规模变大时,如N= 1 024,则每个多播信元自路由目的地址最小的编码代价为1 024bit=128byte,巨大的编码开销使得带宽的利用率变低,信元传输的时延增大,故在信元传输过程中必须采用分级控制。
参考多路径自路由模型[1]建立基于布尔群组集线器的 banyan类交换网络,设N= 2n,N=KG,K= 2k,G=2g,先构造一个K×Kbanyan类网络,这里采用分治banyan类(divide-and-conquer)网络。然后将网络中的2×2交换单元用2G-to-G布尔群组集线器代替。取K= 24,G= 23,可得图3所示的交换结构。该交换结构逐级进行自路由选路,先将分组交换到某个输出群组,而后进行时分输出。该交换结构的多播分组在每个布尔群组集线器中部分扇出。
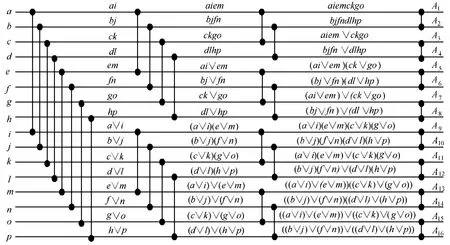
图2 双调循环排序器点线式结构

图3 128×128布尔群组集线器banyan类交换网络
3 部分扇出多播交换阻塞率模型
3.1 部分扇出自路由机制
如图4所示,交换结构的自路由分组格式分为带内控制信息和有效载荷2部分,带内控制信息进行选路控制。自路由方式有2种,一种为每经过一级,该级的有效位被处理后决定输出,所以对于第j,1≤j≤m级,1gj为该级的有效选路信息,由此可实现该控制分组的正确寻路。另一种为每经过一级,其有效位在下一级依然保留被再利用,控制信号在每一级均为 1gjgj+1…gm。在集线器互联的banyan类网络中选择前者,在布尔群组集线器中选择后者。

图4 自路由分组格式
以8-to-3布尔群组集线器为例,由图5(a)和图5(b)对比不难看出,由于输出信息中仍然含有B控制信息,因此多播交换网络采用部分扇出的方式。当有单播加入时,即将图5(a)中的2个I控制位,变为0,1控制位,则图5(b)中输出信息中含有2个B的控制信息,多于图5(a)中输出的B控制信息数,即有一个B没有与I进入过同一个布尔单元,所以其多播性能会下降。假设输入信息中无I信息,那么该多播信息就无法扇出。

图5 8-to-3布尔集线器点线表示
结论:布尔群组集线器,具有部分扇出单播抢占优先的多播能力。对于2n×2n
布尔多播交换结构,根据信息熵理论,其输出地址的任意子集带内控制信息都不能低于2nbit,但可以采用2 1n- 的0,1,,I B四状态带内控制信息来满足二进制比特的带内控制。带内控制信息必须包括每一级的控制信息,这里采用四状态的分割编码(cut-through coding)法[17]。其带内控制信息为
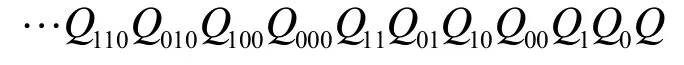
自右向左进行带内控制,前边的位决定后边控制位的分割。对于第一级输入,当Q=B,控制信息从 0端口输出,控制信息从 1端口输出,同时有效载荷扇出。当Q= 0 ,控制信息从0端口输出,且1端口控制信息无效。当Q= 1,控制信息从1端口输出,且0端口控制信息无效。对于第二级输入,当Q0=B时,控制信息从0端口输出,控制信息从1端口输出,同时有效载荷扇出。每一级依次类推,可将分组传输到最终的目的地址。以 23×23banyan网络为例。由图6(a)可见其2个带内控制信号共含有4个B,在无单播与其竞争的情况下,扇出到6个目的端口。当某一2n× 2n布尔多播交换网络输入只有一个带内控制信号为(2n-1)bitB时,可扇出到2n- 1个目的地址。由图6(b)可见,当给网路加入2条单播数据分组,单播数据分组也会与该交换网络中的多播产生竞争,而使多播扇出很少的分组。

图6 banyan类网络多播自路由
结论:布尔多播banyan类交换结构,具有部分扇出单播抢占优先的多播能力。
3.2 多播交换阻塞率模型
单多播混合输入的交换网络,先确定单播与多播争用的布尔群组集线器中多播扇出的情况,扇出个数不同其阻塞率不同。由于布尔群组集线器具有部分扇出特性,因此随着级数的增加,其分组流的个数不断增大,因此其阻塞率不断增大。
第i(1 ≤i≤m)级布尔群组集线器内,单播控制信息不变为,多播控制信息为,其中,iq为二进制数,长度为 1i-,每次当B与I在同一个22×布尔单元时,其后边的控制信息采用2.2节方法进行码分割。
下面分析该结构在不同负载下的阻塞率。假定到达同一输出群组内的分组相互独立,设随机变量代表在某一时隙,到达第i级2 toGG- - 布尔群组集线器复用交换单元某输入/输出群组的分组数目,
XI1为第一级交换单元某输入群组的分组数目,假设单播和多播业务都服从贝努利均匀分布,设单播业务源到达强度的参数λ=p1,则单播业务源在单个时隙里以概率p1到达,设多播业务源到达强度的参数λ=p2,则多播业务源在单个时隙里以概率p2到达,满足条件p1+p2≤ 1,则第一级某一输入群组到达单播分组个数XI1s为
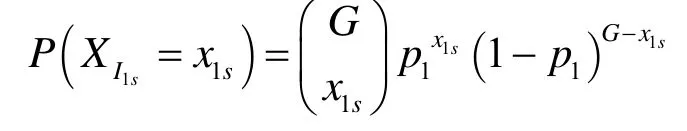
第一级某一输入群组到达多播分组个数1mIX为

其中,p=p1+p2,x1=xs+xm,xs表示单播个数,xm表示多播个数。对于布尔群组集线器到达分组并不是最后的输出分组个数,为更多的扇出多播分组,假设每个多播分组带内控制信号由2k-1个B构成(全B构成),单个布尔集线器中单播的优势导致其多播以一定概率扇出,因为集线器中只有1bit有效位,所以每一个多播分组只能扇出1个或2个分组。对于第一级集线器有输入XI1,YI1独立同分布,假设AI1表示第一级某2G- t o-G布尔群组集线器输入分组数总和,为简化表示,采用DI(di)表示DI=di的概率P(DI=di) 。

∀a1≤ 2G, ∃I∧B= 0 ,I∨B=1, 使 得a1+x1m2+y1m2≤ 2G,其中,x1m=x1m1+x1m2,y1m=y1m1+y1m2,x1m1,y1m1为无扇出的多播分组,x1m2,y1m2为扇出2个分组的多播分组。实际输出的分组的总数a'1为
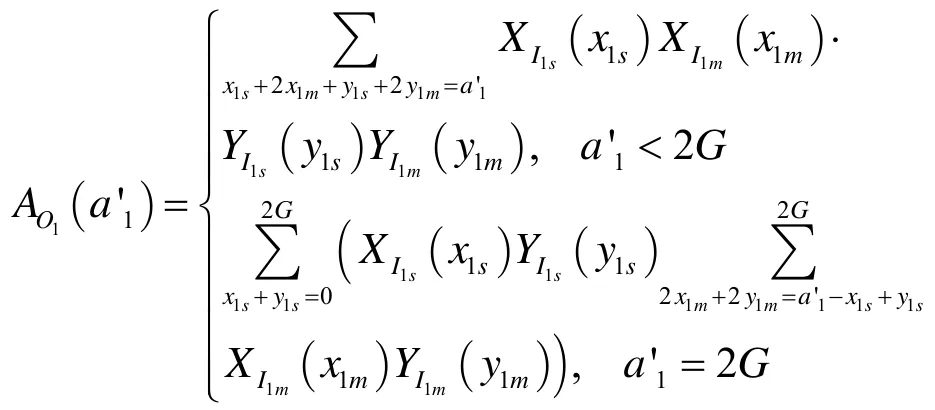
当a'1<2G时多播全被扇出,当a'1=2G时,存在部分多播无扇出的情况。当有z'1<G的分组到达某输出群组,则至少有z'1≤a'1< 2G分组到达该集线器的输入,无路径错误选择,当有z'1=G的分组到达某输出群组,则有a'1=G,a'1=G+1,… ,a'1= 2G个分组竞争该输出群组,则会发生某些分组路径错误选择,导致阻塞。则第一级布尔集线器某输出群组单多播混合分组个数z'1分布为
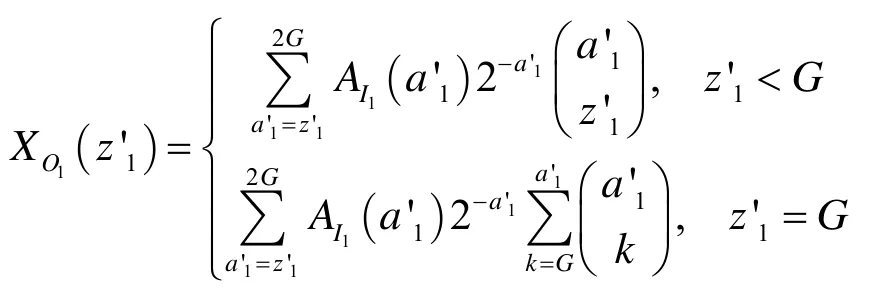
则第一级布尔群组集线器输出单播分组概率分布XO1s(x'1s) 为

其中:

第一级集线器输出多播分组概率XO1m(x'1m)为
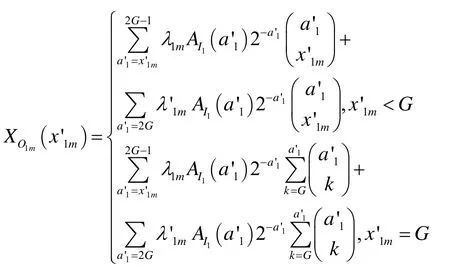
其中,λ1m=1-λ1sλ'1m=1 -λ'1s,已知第i级的输出为第i+ 1 级输入,即XOis,XOim,XOi与XI(i+1)s,XI(i+1)m,XIi+1符合相同分布,实际输入分组总数ai+1服从以下分布:

实际输出的分组总数1'ia+服从以下分布:

第 1i+级布尔集线器某输出群组单多播混合分组个数1'iz+分布为
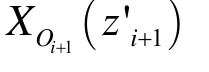

从而推导出第 1i+级布尔群组集线器输出单播分组个数1sOX分布和多播分组个数1mOX分布。迭代可得第k级的布尔集线器某输出群组单多播混合分组个数kOX分布,单播分组个数ksOX分布,多播分组个数kmOX。
单播阻塞率指平均输出单播分组数与平均输入单播分组数的比,得式(1)。
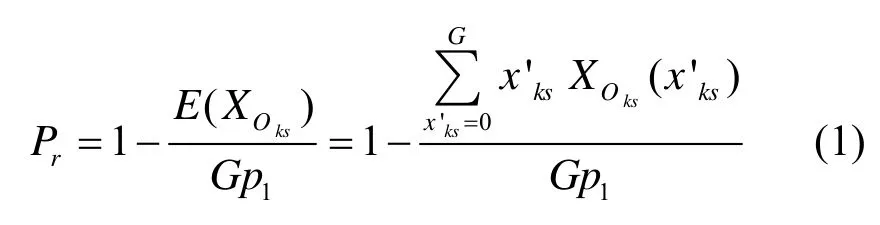
多播阻塞率指平均输出多播分组数与最大输出多播分组数的比,得式(2)。

其中,(k+ 1)Gp2mod(G-Gp1)含义为:全B的带内控制信息,理想最大可扇出 (k+ 1 )Gp2个分组,但受到输出端口数G和单播输入分组数Gp1的影响,最大输出 (k+ 1)Gp2mod(G-Gp1)个多播分组。
多播扇出率指输出多播分组个数与输入多播分组个数的比,得式(3)。
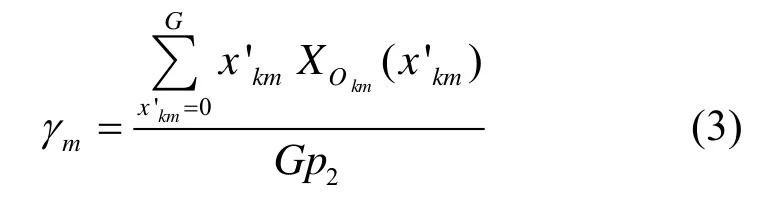
4 仿真实验
本节采用 MATLAB软件对布尔群组集线器自路由交换网络在均匀分布业务源下的单播阻塞率、多播阻塞率和扇出率进行仿真。对于Bernoulli均匀分布业务源,群组业务到达服从二项分布,业务强度采用归一化负载强度表示,对于任意输入群组i,满足用ijλ表示到达输入群组i去往输出群组j的速率。
1) 单播阻塞率仿真
设定多播负载强度p2= 0 .2,单播负载强度0 ≤p1≤1-p2。对于N×N的交换网络,N=KG,K= 2k,G= 2g,在k= 6 的条件下比较G=8,16,32时的单播阻塞率,如图7(a)所示,G越大其阻塞率越小。在G= 1 6的条件下比较k= 4 ,6,8时的阻塞率,如图7(b)所示,k越大其阻塞率越大。该2种条件下,当归一化负载强度>0.6时,其阻塞率大于等于 1 0-2,会造成单播分组的大量错传。
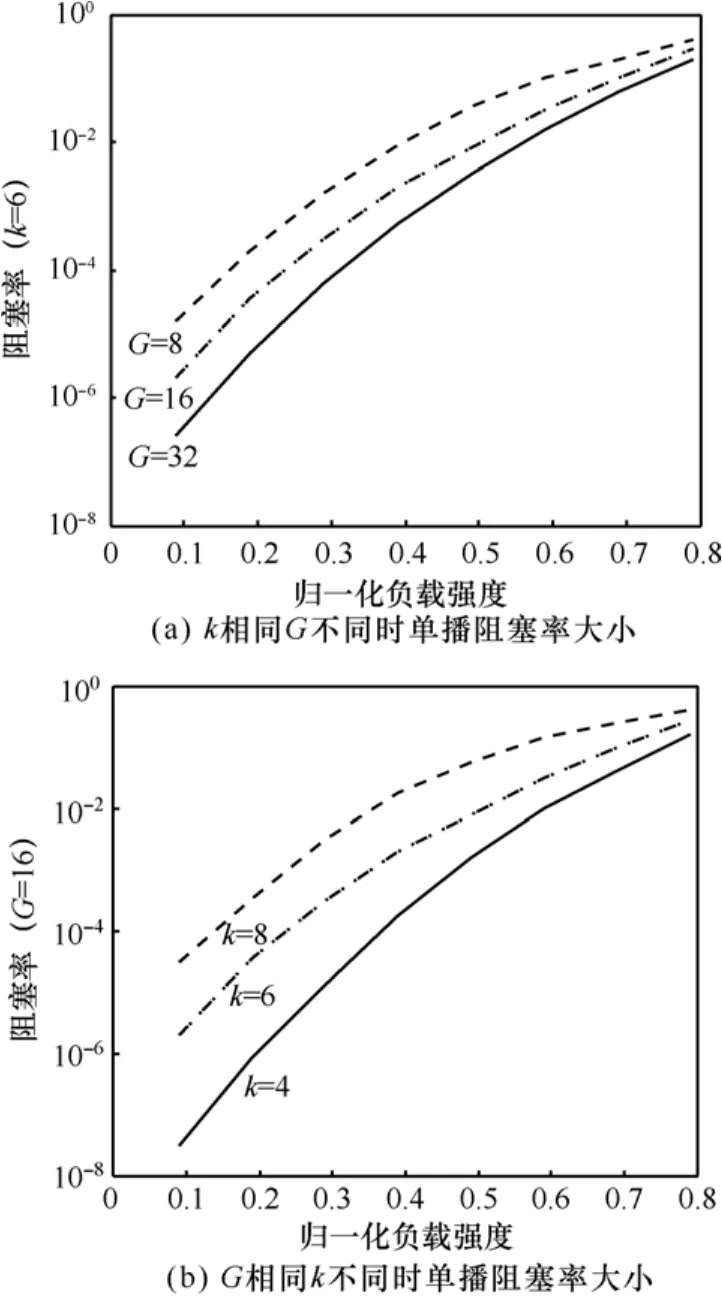
图7 单播阻塞率
原因分析:k决定交换网络的级数,在k不变的情况下,多播负载强度20.2p= ,不同的G时,由于级数相同,其多播分组扇出个数对单播的影响基本相同。但G越大,其xG≤的概率越大,从而减少了xG>时分组在布尔群组集线器中的内部阻塞概率。当G一定时,k越大,交换结构的级数越大,由于多播的扇出特性,随着级数的增加,其多播扇出数就会增加,增加了分组的个数,加大了内部阻塞率。而且每一级由于布尔群组集线器中分组对输出群组的均匀选择,存在一定的路径错传概率,同样加大了单播阻塞率。
2) 多播阻塞率仿真
设定单播负载强度p1= 0 .2,多播负载强度满足0 ≤p2≤1 -p1。在k= 6 的条件下比较G=8,16,32时的多播阻塞率,如图8(a)所示,G越大其阻塞率越小。在G= 1 6的条件下比较k= 4 ,6,8时的多播阻塞率,如图8(b)所示,k越大其阻塞率越大,但k不同时,其阻塞率区别不明显。2种条件下,多播阻塞率小于等于 1 0-2。
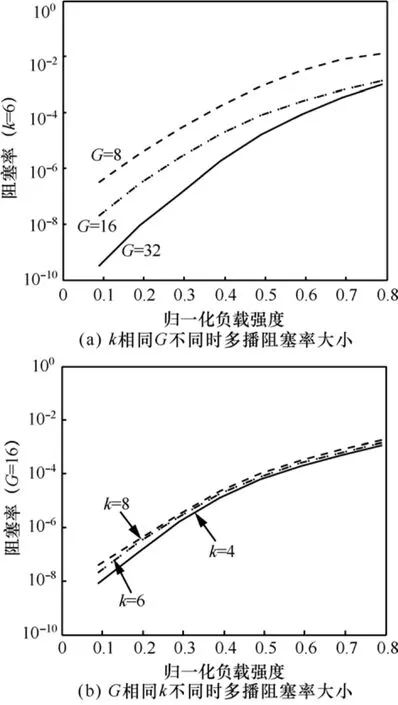
图8 多播阻塞率
原因分析:k决定交换网络的级数,在k不变的情况下,单播负载强度p1= 0 .2,不同的G时,由于级数相同,单播负载强度相同,其单播分组对多播的影响基本相同。但G越大,其x≤G的概率越大,从而减少了x>G时分组在布尔集线器中的内部阻塞概率。当G一定时,k越大,交换结构的级数越大,但由于多播的扇出特性,当级数大于等于4时,负载p2≥ 0 .2时,其4次扇出的多播分组个数就接近G- 0 .2G= 0 .8G,后几级的多播扇出会很小,而对于式(2),需要做模 (G-Gp1)运算,所以k= 4 ,6,8时,其阻塞率区别不明显。
3) 多播扇出率仿真
设定单播负载强度p1= 0 .2,多播负载强度0 ≤p2≤ 1 -p1,在k= 6 的条件下,比较G=8,16,32时的多播扇出率,如图9(a)所示,归一化负载强度为0.1时,多播扇出率接近7,G越大其扇出率越大,多播归一化负载强度接近0.8时,其扇出率都趋近于1,但G不同时,其多播扇出率区别不明显。在G=16的条件下,比较k= 4 ,6,8时的多播扇出率,如图9(b)所示,k越大其多播扇出率越大。

图9 多播扇出率
原因分析:k决定交换网络的级数,在k不变的情况下,单播负载强度10.2p= ,不同的G时,由于级数相同,单播负载强度相同,其单播分组对多播的影响基本相同。G不同,但多播分组的输入分组个数和输出分组个数同等比例增加,所以扇出率变化不明显。当G变大时,xG≤的概率变大,从而减少了xG>的概率,减少了分组在布尔集线器中的内部阻塞概率,使式(3)分子变大,所以扇出率变大。当G一定时,k越大,交换结构的级数越大,由于多播的扇出特性,当级数变大时,多播就会有更多的扇出分组, 8k= 比 6k= 时多了两级扇出, 6k= 比 4k= 时多了两级扇出,所以随着k的变大,其扇出率明显变大。当多播负载非常小时,其多播可以完全扇出,其扇出率正比于k+ 1,所以当归一化负载强度为0.1时,k= 8 ,6,4时,多播扇出率分别接近于9,7,5。
4) 多播时延仿真
时延分为分组平均时延Da和分组最大时延Dm。若交换系统在一定时间内交换的分组数为n,di代表第i,1≤i≤n个分组的时延,那么Da和Dm描述为
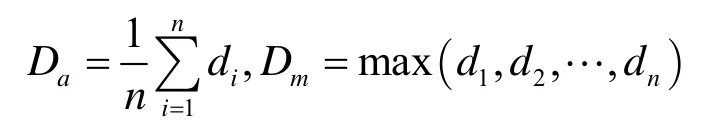
分组的时延主要由分组经过2×2布尔单元个数决定,假设分组每经过一个2×2布尔单元的时延为Δd,一般在ns级。
在k= 6 的条件下比较G= 8 ,16,32时的时延,如图 10(a)所示,G越小时延越小。在负载强度小于等于 0.5时,其时延增长速度Tv的关系为Tv(G=32)<Tv(G=16)<Tv(G=8),在负载强度>0.5时,其时延增长速度Tv的关系为Tv(G=32)>Tv(G=16)>Tv(G=8)。在G= 1 6的条件下比较k= 8 ,6,4时的时延,如图10(b)所示,k越小其时延越小。且负载强度在(0,0.8]范围内时,k不同,时延增长速度Tv变化不明显。

图10 多播时延
原因分析:在阻塞率相同的情况下,时延主要受2×2布尔单元级数的影响,该级数由集线器中2×2布尔单元的级数和banyan类网络级数相乘得到。G不变,G越大,集线器中2×2布尔单元的级数越大,2×2布尔单元的总级数越大,所以时延变大。对于图10(a),当负载强度小于等于0.5时,由于G= 3 2的阻塞率远远小于G= 1 6,G= 8 ,因此Tv(G=32)最小。当负载强度大于 0.5时,由于G= 3 2的阻塞率与G=16,G=8在相同的数量级,但G=32时2×2排序器级数最大,所以Tv(G=32)最大。G不变,k越大,2×2交换单元的总级数越大,时延越大,而由图8(b)可知,k不同时,其阻塞率变化不明显,因此在图10(b)中时延增长速度Tv无明显变化。不论何种G,k参数的交换结构,其时延总小于某个定值。例如:当G= 3 2,k=6时,时延 小 于等于Dmax,约等于1 8 7.5Δt,当G=16,k= 8 时,时延 小 于等于Dmax,约等于1 8 0Δt。
不同的业务对带宽、丢失率、时延、抖动等QoS需求是不同的,如电子邮件对实时性要求低,但对丢失率要求高,丢失后必须重传;实时流媒体业务对实时性要求高,一定丢失率下不影响服务质量。该单多播混合输入部分扇出多播交换模型,当单播负载强度控制在一定范围内时,如p1≤ 0 .2时,其多播阻塞率小于等于 1 0-2,所以该交换结构可以满足某些网络场景的应用,其多播时延总小于某个定值,且该定值在百纳秒量级,所以该交换结构能够为到达业务提供时延上限保障。
5 结束语
本文的阻塞率模型是部分扇出多播模型,由于单播抢占或阻塞,在单个交换节点扇出率小的多播分组可在下一个交换节点中再次进行部分扇出。本文假设多播的带内控制信息为全B,即对所有输出端口均有扇出,该假设忽略了多播对输出端口集的限制,下一步工作,基于可控多播输出端口集进行多播扇出模型的建立,该模型需要考虑每一级是否扇出的问题。
[1] LABOVITZ C, IEKEL-JOHNSON S, MCPHERSO D. Internet inter-domain traffic[A]. Proc of the ACM SIGCOMM[C]. New Delhi,India, 2010, 75-86.
[2] 中国互联网络信息中心. 中国互联网络发展状况统计报告[EB/OL].http://www.cnnic.net.cn/dtygg/dtgg/201201/t20120116_23667.html,2011.China Internet Network Information Center. Statistical report of China Internet network development status[EB/OL].http://www.cnnic.net.cn/dtygg/dtgg/201201/t20120116_23667.html, 2011.
[3] HUANG A, KNAUER S. Starlite: a wideband digital switch[A]. Proc of Globecom[C]. Atlanta, GA, 1984. 121-125.
[4] DEERING S, CHERITON D. Multicast routing in datagram internetworks and extended LANs[J]. ACM Transactions on Computer Systems, 1990, 8(2):85-110.
[5] ERIKSSON H. Mbone: the multicast backbone[J]. Communication of the ACM, 1994, 37(8):54-55.
[6] LEE T T. Non-blocking copy networks for multicast packet switching[J]. IEEE Journal on Selected Areas in Communications, 1988, 6(9):1445-1467.
[7] GUO M H, CHANG R S. Multicast ATM switches based on input cells scheduling[A]. Proc of APCC[C]. Sydney, Australia, 1997. 1629-1632.
[8] YEH Y S, HLUCHYTJ M G, ACAMPORA A. The knockout switch:asimple, modular architecture for high-performance packet switching[J].IEEE Journal on Selected Areas in Communications, 1987, 5(8): 1274-1283.
[9] YANG Y, MASSON G M. Broadcast ring sandwich networks[J].IEEE Trans Computers, 1995, 44(10):1169-1180.
[10] JASTRZEBSKI A, KUBALE M. Rearrangeability in multicast clos networks is np-complete[A]. 2010 2nd International Conference on Information Technology (ICIT)[C]. 2010. 183-186.
[11] PAN D, YANG Y. FIFO-based multicast scheduling algorithm for virtual output queued packet switches[J]. IEEE Transactions on Computers, 2005, 54(10):1283-1297.
[12] 胡曦明. 有效支持IPTV业务的扇出无关交换结构[D]. 郑州: 信息工程大学, 2007. 29-49.HU X M. Fanout-free Switch Fabric to Support IPTV Business[D].Zhengzhou: Infromation Engeering University, 2007. 29-49.
[13] HU H C, LIN P, GUO Y F. Integrated uni- and multicast traffic scheduling in buffered crossbar switches[A]. 3rd Intentional Conference on Communications and Networking in China (ChinaCOM’08)[C].Hangzhou, China, 2008. 66-72.
[14] 兰巨龙. 可重构信息通信基础网络体系研究[R]. 国家重点基础研究发展计划(973计划)项目计划任务书, 2011.LAN J L. Research on Foundition Network System of Reconfigurable Information Communication[R]. Planning Task Document of National Basic Research Program of China(973 Program), 2011.
[15] 刘莹, 徐恪. Internet 多播体系结构[M]. 北京:科学出版社, 2008.LIU Y, XU K. Internet Multicast Archithecture[M].Beijing: Science Press, 2008.
[16] LI S Y R. Unified algebraic theory of sorting, routing, multicasting,and concentration networks[J]. IEEE Transactions on Communications,2010, 58(1):247-256.
[17] LI S Y R. Algebraic Switching Theory and Broadband Applications[M]. San Diego, CA, USA: Academic Press, 2001. 281-321.
[18] 李挥, 何伟, 伊鹏. 排序集线器多级互连交换结构的多路径自路由模型[J]. 电子学报, 2008, 36(1):1-8.LI H, HE W, YI P,et al. Modeling multi-path self-routing switching structure from multistage interconnection of sorting concentrators[J].Acta Electronica Sinica, 2008, 36(1):1-8.
