基于ANSYS 的穿透裂纹三维板数值分析
2012-08-01李成英
高 健 李成英
(辽宁工业大学,辽宁锦州 121000)
0 引言
裂纹广泛存在于工程构件中,其对工程结构的破坏作用越来越受到重视,各国学者在大量实验、分析和数据基础上建立了一些裂纹模型和判定准则,在工程中得到了比较广泛的应用。随着近代计算机技术的发展,有限元方法逐渐渗透到了构件裂纹分析当中。带裂纹的构件在外力作用下,材料内部会产生应力集中,裂尖附近材料发生塑性屈服[1],并在构件最薄弱的裂尖处首先开裂,使构件在低于实际强度很多的情况下发生破坏,所以研究含裂纹材料的开裂条件是问题的关键,由此引入了断裂力学中应力强度因子的概念。
应力强度因子K反映了裂纹尖端应力场的强弱,通过应力强度因子与材料断裂韧性KIC的比较作为裂纹扩展发生的判据。各国对应力强度因子的研究不断深入,我国航空研究院编制的应力强度因子手册对各种规律裂纹形式给出了较为精确的解析解。本文以不同位置穿透裂纹为例,运用ANSYS中KCALC命令和J积分命令流程序来模拟推导应力强度因子计算。
1 穿透裂纹板模型
矩形板尺寸 2a=254,2b=304.8,c=12.7,裂纹 2t=50.8,受压荷载 σ=0.01 MPa,弹性模量 E=24 GPa,泊松比 γ=0.2。图1表示穿透裂纹板建立的位置、尺寸及荷载信息。

图1 中心穿透裂纹矩形板
2 裂纹板建模
在线弹性问题中,裂纹尖端附近的应力场可统一为:

且有:

其中,r为任一点到裂纹尖端距离;σ为该点应力张量,根据式(1)当r趋于0时,对应的σ趋于无穷大,所以裂纹尖端处的应力与应变存在奇异性。ANSYS在进行模拟时,为了选取应变奇异点,相应的裂纹面需与其一致,即围绕裂纹顶点的有限元单元应选取带中间节点的二次奇异单元,并将其中节点放到距尖端1/4 处[2]。
ANSYS建模主要思路:对三维八节点实体Solid65单元通过添加1/4位置的中间节点转化成Solid95单元,编辑宏程序*CREATE,FRACT,MAC[3]来实现。穿透裂纹矩形板模型为 X,Y 轴双向对称,故取1/4建模分析即可。划分网格时对裂纹周围需采用特殊划分处理。
建模具体过程如下[4]:
1)在裂纹前缘上,单元的大小取决于局部曲率的数值。本文采用沿圆环状弯曲裂纹前缘,在15°~30°内设置一个单元。裂纹尖端周围单元建立如图2~图5所示。

图2 裂尖一层单元前视图

图3 裂尖一层单元等轴侧视图

图4 裂尖沿圆环多层单元前视图

图5 裂尖沿圆环多层单元等轴侧视图
2)剩余节点中每8个相邻节点形成一个单元,将1/4板模型建立完整,如图6,图7所示。

图6 1/4板单元平视图

图7 1/4板单元等轴侧视图

图8 1/4板单元施加约束及荷载平视图

图9 1/4板单元施加约束及荷载等轴侧视图
3)1/4板单元建立后施加双向对称约束,并对上边和右边施加UX,UY,UZ简支约束。对裂纹处不施加任何约束来模拟穿透裂纹的力学特性。板表面均匀压力荷载及约束如图8,图9所示。
3 计算方法及理论依据
3.1 J积分
J积分[5]为围绕裂纹尖端的围线积分,这个积分值与积分路径无关,为一常数,并反映了裂纹尖端应力应变场强度的量。
J积分表达式:

式中:Γ——围绕裂纹尖端的一条任意反时针回路,起端始于裂纹下表面,末端终于裂纹的上表面;
W——弹塑性条件下,回路Γ上任意点(x,y)的应变能密
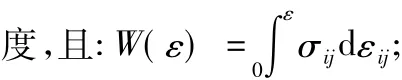
Ti——回路Γ上任意点(x,y)处的应力分量;
ui——回路Γ上任意点(x,y)处的位移分量;
ds——回路Γ上的弧元,在ANSYS中通过编写APDL命令流来完成任意路径下的积分求值过程。
3.2 KCALC 命令
ANSYS软件本身具有计算断裂力学参数的功能。可以采用后处理器POST1中的KCALC命令(Main Menu>General Postproc>Nodal Calcs> Stress Int Factr)或编写 KCALC,KPLAN,MAT,KCSYM,KLOCPR命令流来计算复合型断裂模式中的应力强度因子(KⅠ,KⅡ,KⅢ)。后者操作更为简便。
3.3 矩形板承受均匀表面力的解析解
厚度为c的等厚矩形板,带有一条或两条(共线)裂纹,边界条件为四边简支情况下,在板面上每单位面积承受均匀表面荷载σ,则其最大应力强度因子解析解[6,7](在裂纹尖端处)可统一表达为:

其中,p对应三种不同位置裂纹的表达式为:
中间裂纹:

单边裂纹:

双边裂纹:

其中,v为泊松比。
4 误差分析
为了验证应力强度因子模拟的计算精度和可靠性,选取5种阶梯荷载分别计算。模拟结果与解析解对比,得到三种不同位置裂纹的计算误差如表1,表2所示。

图10函数(f)取值图

表1 中心裂纹计算结果
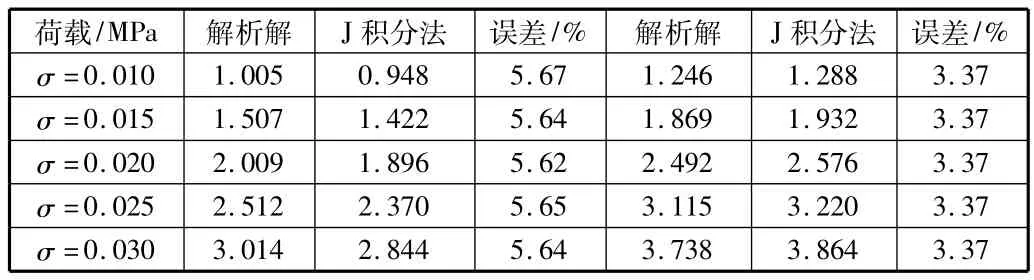
表2 单、双边裂纹计算结果
5 结语
通过比较,运用ANSYS对穿透裂纹板均匀压力荷载下的应力强度因子计算是准确的、可靠的。通过ANSYS来计算应力强度因子可以大大提高计算效率,应用于工程实践。以板为基础,修改构件尺寸及荷载,可以实现对不同构件和不同荷载作用下的断裂参数计算,为三维构件的裂纹扩展研究打下理论基础。
[1] 康颖安.断裂力学的发展与研究现状[J].湖南工程学院学报,2006,16(1):39-42.
[2] 葛润广,岳 烨,毛洲明.基于ANSYS的应力强度因子计算[J].湖南城市学院学报,2009,18(2):10-12.
[3] 邢静忠,王永岗.ANSYS7.0分析实例与工程应用[M].北京:机械工业出版社,2004.
[4] 瞿伟廉,鲁丽君,李 明.带三维穿透裂纹结构的有限元实体建模方法[J].武汉理工大学学报,2008,30(1):87-90.
[5] 程 靳,赵树山.断裂力学[M].北京:科学出版社,2006.
[6] 中国航空研究院.应力强度因子手册[M].北京:科学出版社,1993.
[7] Sih,G.C..Bending of a Cracked Plate under a Single Couple,Lehigh University Technical Report,1962.
