图的最大拉普拉斯特征值的上界

乔晓云

(山西大学商务学院理学系，太原030031)

设G=(V，E)是n阶简单图，其顶点集为V(G)={ν1，ν2，…，νn}，dG(νi)为顶点 νi在图G中的度数，简记为dνi，并假定对顶点进行适当排序使得度序列满足dν1≥dν2≥…≥dνn.对任意的u∈V，它的相邻点度的平均值称为u的平均二次度，记为mu，即mu=记D(G)=diag(dν1，dν2，…，dνn)和A(G)分别是图G的度对角矩阵和邻接矩阵，则图G的拉普拉斯矩阵定义为L(G)=D(G)-A(G).易证L(G)是一个半正定的、实对称矩阵，且它的每一行的行和为0，从而可以假设它的特征值为:λ1(G)≥λ2(G)≥…λn(G)=0，其中λ1(G)称为图G的最大拉普拉斯特征值。研究拉普拉斯矩阵的特征值有着重要的理论和实际意义，它在计算机网络、物理、化学和生物中有着广泛而重要的应用[1-2]，因而一直受到关注。近年来关于拉普拉斯特征值的研究，特别是最大拉普拉斯特征值的上界的估计有了不少代表性的结果。

2001 年，J.S.Li和 Y.L.Pan[3]给出了:

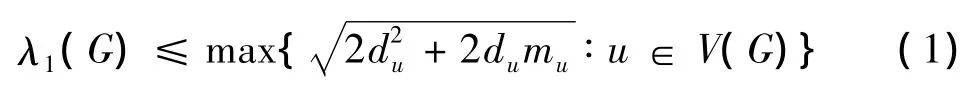
其中等式成立当且仅当G为正则偶图。

2004 年，X.D.Zhang[4]给出了

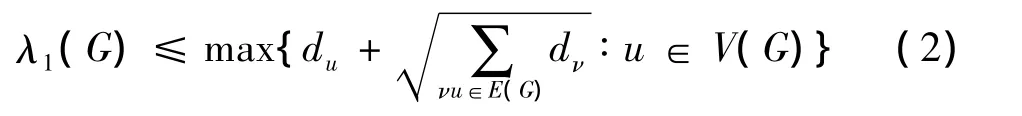
其中等式成立当且仅当G为正则偶图或半正则偶图。

本文的目标是利用图的顶点度，平均二次度结合非负矩阵谱理论给出图的最大拉普拉斯特征值的上界估计式，并和这些已知上界估计式进行比较，说明在某些情况下优于已知结果。本文未定义而直接引用的术语和符号参见文献[5].

1 引理和主要结果

设K(G)=D(G)+A(G)，称为G的拟拉普拉斯矩阵.熟知当G是连通图时，K(G)是非负，实对称和不可约矩阵。记ρ(K)是K(G)的谱半径。

引理1[6]设M为非负不可约矩阵，ρ(M)为M的谱半径，则存在一个正特征向量X使得MX=ρ(M)X.

引理 2[7]设G=(V，E)是n阶连通图，则λ1(G)≤ρ(K)，其中等式成立当且仅当G是偶图。

引理3[8]设G=(V，E)为r正则图，则 ρ(K)=2r.

定理1 设G是简单连通图，则有:

其中等式成立当且仅当G为正则偶图。

证明 由D的定义可知:V(G)).令，则矩阵M的第(u，ν)个元素为:

由G是简单连通图易知M是非负不可约的。由引理1 可知:可设向量X=(x1，x2，…，xn)T为M的对应于特征值ρ(M)的正特征向量，即MX=

由Cauchy-Schwarz不等式可知:

故存在u∈V(G)，使得:(ρ(M)-du)2-所以由引理2可知:

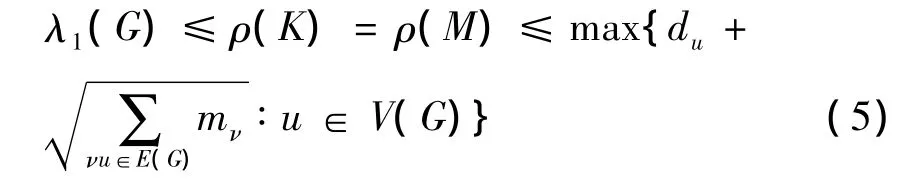
当式(3)中等式成立时，以上证明过程中的不等式均为等式，则存在u∈V(G)，使得 ρ(M)=根据式(4)可知，故存在w∈V(G)但w≠u，使得，即:

由引理2知G为偶图。假设(S，T)是V的一个分割，不妨设u为T中的最大度点，u'为T中的最小度点，则有，且，结合取遍V(G)中的所有顶点)是一个常数，所以du=du'，即T中的顶点度数相等。所以:

反之，当G为正则偶图时，由引理2，3易证式(3)中等式成立。

2 注记和图例

一般来说，本文得到的上界式(3)与前面所提及的已知上界估计式在一般情况下是不可比较的。Zhang在文献[4]中指出式(2)总优于式(1)。下面通过图1来说明本文得到的新上界式(3)在某些情况下优于式(2)。各上界值如表1所示。

图1 λ1(G1)上界比较图Fig.1 A comparative graph of the upper bound of λ1(G1)

表1 λ1(G1)上界的值Tab.1 The values of the upper bound of λ1(G1)

[1]MERRIS R.A Survey of graph Laplacians[J].Linear and Multilinear Algebra，1995，39(3):19-31.

[2]姜誉，方滨兴.大型ISP网络拓扑多点测量及其特征分析实例[J].软件学报，2005，16(5):846-856.

[3]LI J S，PAN Y L.De Caens inequality and bounds on the largest Laplacian eigenvalue of a graph[J].Linear Algebra Appl，2001，328(4):153-160.

[4]ZHANG X D.Two sharp upper bounds for the Laplacian eigenvalues[J].Linear Algebra Appl，2004，376(3):207-213.

[5]邦迪J A.图论及其应用[M].北京:科学出版社，1984.

[6]HORN R A，JOHNSON C R.Matrix Analysis[M].New York:Cambridge University Press，1985.

[7]PAN Y L.Sharp upper bounds for the Laplacian graph eigenvalues[J].Linear Algebra Appl，2002，355(2):287-295.

[8]LIU H Q，LU M，TIAN F.On the Laplacian spectral radius of a graph[J].Linear Algebra Appl，2004，376(4):135-141.

[9]张海霞，魏海燕.按树的最大Laplace特征值对树进行排序[J].太原科技大学学报，2009，30(6):523-527.

[10]张海霞，谢秀梅.关于树的Laplace特征值上界的估计[J].太原科技大学学报，2007，28(3):205-207.

[11]张海霞，薛海连.对图的最大Laplace特征值上界估计的两个新结果[J].太原科技大学学报，2007，28(1):60-63.