对皮江法炼镁升温过程的数值模拟

2012-08-01孙晓思崔小朝林金保

太原科技大学学报 2012年1期

孙晓思，崔小朝，林金保

(太原科技大学应用科学学院，太原030024)

金属镁作为“21世纪的绿色工程材料”[1-2]，发展至今已有203年的历史。镁及镁合金以其轻质，比强度高、比刚度高、导热性优良、电磁屏蔽性好、抗震、阻尼性好、耐凹陷性好、节能环保，尺寸稳定性高、耐腐蚀以及强大的储氢优势等优良特性[3-5]被广泛应用于汽车工业、3C产业、航空航天领域、冶金业、化学化工领域、现代兵器工业、核工业以及其他日常消费品领域中[6-7]。

金属镁的制备方法主要分为电解法和热还原法。在我国，热还原法中的皮江法占据主导地位。然而皮江法炼镁仍存在很多缺陷，例如还原阶段热损失以及能耗比较大、污染环境等。因此研究皮江法还原阶段球团的升温过程进而分析影响球团升温的各种因素，对优化炼镁工艺具有重要意义。以往关于皮江法升温过程的研究主要集中在借助PDTD有限差分方法实现对球团温度场的数值模拟，例如夏德宏[8]等在2005年对金属镁皮江法还原工艺进行的热过程模拟。从以往研究中不难发现，PDTD法过程繁琐，需要对升温过程中的诸多因素理想化处理，客观上导致了模拟结果的误差性。本文借助于Matlab数值分析软件以及MSC.Marc有限元分析软件，得到皮江法炼镁的还原阶段球团的升温过程的解析解和数值解，减少了繁冗的分析过程，通过与实际生产数值的对比，验证了其结果的可靠性。

1 数值模拟方法描述

1.1 炼镁原料热物性参数

根据实际生产核桃状球团的平均直径取Dr=2.23×10-2m，当量半径r0=1.71 ×10-2m，球团在反应区内的环境温度为TW=1 200℃，球团初始温度T0=25 ℃[9].结合文献[10]，确定球团热容 ρCp=0.373 ×106J/(kg·K)，辐射系数 ε =0.57，有效导热系数 λ =1.30 W/(m·K).

根据辐射传热系数计算公式[11]

式中:hr——球团表面辐射传热系数，W/(m2·K);

ε——球团表面辐射系数;

σ——Stefan-Boltzmann常数，其值为 5.67 ×10-8W/(m2·K4);

TW——球团在反应区内的环境温度，K;

T0——球团初始温度，K.

在环境温度与球团表面温度相差11℃左右时，计算环境温度为1 150℃时球团表面辐射传热系数为:hr=3.68 ×102W/(m2·K)[9].

1.2 球团基本传热方程

球团在加热过程中未发生化学反应(未达反应温度时)，也就是无内热源，球团的导热微分方程可通过热传导的基本微分方程来推算:

式中:r——球团半径，m;

T——温度，K;

αc——导温系数

λ——有效导热系数，W/(m·K);

ρCp——等压热容，J/(mol·K).

1.3 边界及初始条件

式中:hr——外部给热系数，W/(m2·K)，这里只有辐射给热;

Ts——球团外壳温度，K;

Tw——环境温度，K;

r0——球团的有效半径。

2 模拟结果及分析

2.1 解析法对球团升温过程的模拟

2.1.1 温度分布函数方程

在皮江法炼镁的还原阶段，球团内部不同区域的温度取决于球团自身热物性参数、反应区环境温度等。由于球团自身的热物性参数随温度的变化而不断变化，所以还原阶段球团内部温度与时间、空间、密度、传热系数等有关。实际生产中球团在真空条件下进行还原反应中无对流给热，球团导热系数为3.26×10-2W/(m·K)，球团周围的辐射传热基本上是均匀的，而且球团内部各处的导热系数、热容不随时间、位置发生变化，在这种情况球团的导热可认为是一维不稳定导热，因此球团内的温度分布只是半径和时间的函数。

根据文献[9]，得到半径为r0的球团在真空环境温度TW下的温度分布函数:

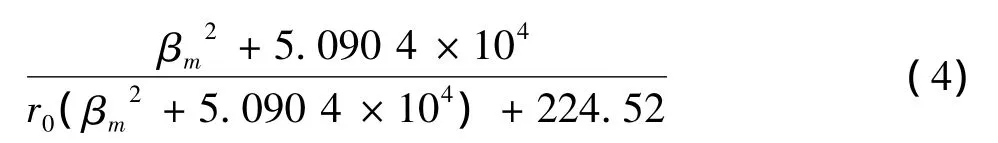
2.1.2 对温度分布函数的求解

在(4)式中βm是下列方程的正根

查表得到βm的前六个值[12]，如表1所示:

表1 方程(4)的前六个根Tab.1 The six prior roots of the forth equation

球团在加热过程中的温度分布可以用无穷级数表示，一般可用计算值的前六项之和近似表达[9]。

通过Matlab编程有限循环语句很容易实现对函数(3)的求解，其结果如图1所示。

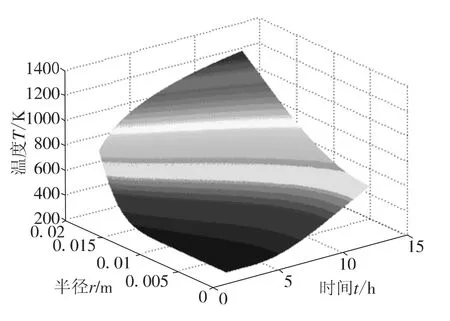
图1 皮江法炼镁还原阶段的温度分布Fig.1 The distribution of temperature during the redoxomorphic stage of the silicon-thermo-reduction

2.2 有限元法对球团升温过程的模拟

2.2.1 传热模型

利用有限元分析软件，应用式(2)作为球团温度分析的基本热传导方程。

2.2.2 对传热模型的模拟结果

根据有限元分析中的结构对称性原则，所以选取二分之一半圆作为分析面。

运算结果如图2所示。

2.3 结果比较分析

将上述解析法与数值法的模拟结果对比情况可由表2表示。

图2 还原阶段球团分别在第40、68、100、101、102、103步时的温度场分布Fig.2 The distribution of temperature at the step 40，68，100，101，102b and 103 during the redoxomorphic stage

通过表2数据可以得出:通过函数解析法求得的解析解升温速度缓慢，球心与表面间温差较大;相比之下，通过数值法求得的数值解升温速度大大增加，球心与表面间温差也大大缩小。结合炼镁工业生产实际，数值解相对较为理想，与实际情况较为吻合。

分析原因，具体如下:

(1)利用解析法求解解析解的过程中，忽略了传热系数随时间变化等因素，从而导致了球团升温缓慢、内外温差大。

(2)即使就相对理想的数值解而言，球心与表面仍存在温差，加热时间达到12 h后表面温度仍然距离理想的还原温度1 200℃有微小差距。造成此结果的原因有两个，一是球团由煅白、硅铁、萤石粉按一定比例混合压制而成，就其构成球团的物质本身传热系数就较低，传热效果不是十分理想，导致升温缓慢;二是传统的皮江法炼镁工艺还原阶段采用还原炉外部加热方式，热能通过炉壁热传导以及热辐射传给球团，过程中不可避免地增加了大量热损失，造成了升温缓慢，以及传统加热普遍存在的“冷中心”的缺陷。

表2 对球团还原过程温度场模拟的解析解与数值解结果比较Tab.2 The comparison between analytic solution and numerical solution of temperature during the redoxomorphic stage of the silicon-thermo-reduction