具有风险的供应商选择中延迟成本的计算算法

李补喜，蔚晓娇

(1.山西大学工商管理研究所，太原030006;2.山西大学数学科学学院，太原030006)

供应商，是指可以为企业提供原材料、设备及其他资源的企业。它可以是生产企业，也可以是流通企业。供应商对企业的生产和发展起着非常重要的作用。供应商选择是供应链及其风险管理中的一个经典决策问题。企业在选择供应商时不仅考虑各个供应商提供的产品的质量、价格、送货的及时性，同时，在面对各种不确定的情况下，还要考虑采购过程可能碰到的各种风险，如，因地震、自然灾害等造成供应商不能及时送货从而导致企业生产中断，不能按时满足顾客需求，由此产生企业违约，给企业带来损失[1-3]。此外，为了降低风险，企业在全面考虑各种因素的基础上，通常选择从多个供应商采购不同数量的货物。因此，在有不确定性的情况下，进行供应商选择决策时，需要比较各种可能情形下的成本，通常选择成本或风险价值(VAR或CVAR[4-5])最低的供应商组合。然而，实际中，供应商选择中面临的不确定的情况复杂，供应商的不同采购组合情景数量很大，如10个供应商，每个供应商的不确定因素有10种可能，这时供应商的所有可能组合有100亿种。要对如此庞大的组合比较相应的成本，进而选择出成本最低的供应商组合，其计算工作量巨大。因此如何处理供应商选择过程中碰到的数据量大、可能情景多，即如何减少计算工作量，是一个十分重要的问题。本文的目的在于考虑具有离散指数分布延迟风险的供应商选择问题。许多文献考虑了供应商选择模型，或者是单周期模型，或者是多周期模型[6-9]。还有文献考虑了供应商选择评价指标体系[10]。而本文目的既不在于建立供应商选择模型，也不在于对供应商选择进行评价，而是利用数学模型将数量庞大的情景转化为数量较少的另一种情景。

2 取值组合的重新划分

首先给出一个定义:

定义 若X为连续型随机变量，Y为离散型随机变量。如果对于任何整数k，Y的概率分布满足:P(Y=k)=P(k≤X＜k+1)

则称Y为连续型随机变量X的离散化随机变量。

假设一个生产商为顾客不同订单组装生产多种类型的产品，生产使用的零部件是向多个供应商采购的。每个供应商能为生产商提供所需的定制部件。然而，供应商的供应能力不同，并且提供零部件的价格，质量以及按时交货的可能性方面不同。设I={1，2，…，m}为m个供应商的集合，每个供应商单位周期(如天)单位产品的延迟惩罚成本不同，假设供应商i的单位周期单位产品的延迟成本为ei.同时，假设不同供应商的延迟周期相互独立，且供应商i的延迟周期数Yi是指数分布的离散化随机变量，其最大延迟周期为ni，对应的指数分布为Xi.则，对于任何非负整数k＜ni，有:

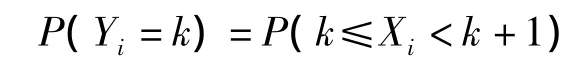
且P(Yi=ni)=P(ni≤Xi)

在具有延迟风险的供应商选择决策中，从不同供应商订购不同数量零部件(设从供应商i订购的数量为zi，(z1，z2，L，zm)是决策变量)的延迟成本为:

显然，由于Yi为随机变量，若要选择供应商，需要穷尽所有可能的供应商的延迟组合(Y1，Y2，L，Ym)，并计算不同供应商组合下的延迟成本(1)并进行比较。若供应商的数量较大(如m=10)，且每一供应商的可能延迟周期数较大(如ni=10)，那么，供应商的延迟组合(Y1，Y2，L，Ym)数量为 1110。显然，这会导致供应商选择模型的计算工作量很大。

为了解决上述组合数量庞大所导致的计算量问题，需要将大量的原始组合从不同视角进行重新分组，划分为组合数量较少的情形。为此，考虑所有供应商总延迟的离散化随机变量，记为Y，定义如下:

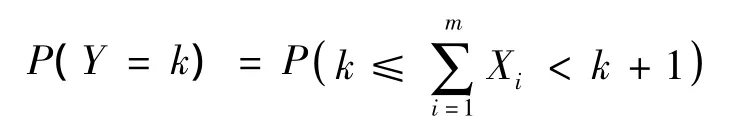
在这种情况下，如果m=10且ni=10，那么，可能的情形只有101种，由此降低供应商延迟的可能情形的数量。这时，用Y估计的每一可能情形下的延迟成本。

需要指出，Y与不同，二者之间的差异及其对延迟成本的影响，还有待研究。本文着重强调大样本问题转化为小样本问题的简化方法。

2 延迟成本的估计

定理1 设随机变量Xi(i=1，2，…，m)服从参数为 λi(i=1，2，…，m)的指数分布，且Xi(i=1，2，…，m)相互独立。

(1)若λ1=λ2=… =λm=λ，则服从Ga(m，λ)，其密度函数为:

(2)若 λi(i=1，2，…，m)互不相同，则X=的密度函数为:

证明 (1)的证明利用卷积公式容易得到，下面给出(2)的证明过程。

利用数学归纳法证明。

当m=2时，易证结论成立。

假设当m=k-1时，结论成立，即的密度函数为:

当m=k时，的密度函数为:

故结论成立。

因此，当λ1=λ2=…=λm=λ时，

当 λi(i=1，2，…，m)互不相同时，

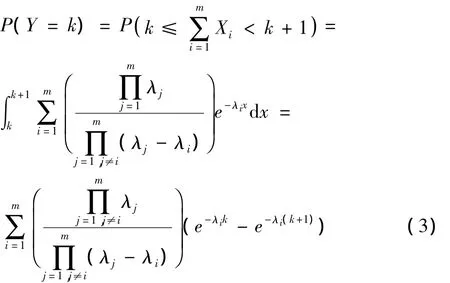
上述定理将不同供应商的延迟周期转化为所有供应商的总延迟周期。这意味着，不同供应商延迟周期的组合，将以总和的形式加以表现。因此，这为不同供应商延迟周期的所有可能情形(组合数量为)转化为所有供应商总的延迟周期的可能情形(组合数量为()提供了基础，显然，可能情形的数量大大降低。

同时，上述定理也为所有供应商总的延迟周期的每一取值出现的概率提供了计算基础。

定理2 设供应商i(i=1，2，…，m)的延迟周期为非负连续型随机变量Xi(i=1，2，…，m)的离散化随机变量Yi(i=1，2，…，m)，其最大延迟周期为ni(i=1，2，…，m)。且假定，Xi(i=1，2，…，m)相互独立。若zi为从供应商i订购的产品数量，ei为供应商i的单位周期单位产品的延迟成本。则对于任意非负整数，在的情形下，从全部供应商订购零部件总平均延迟成本为:

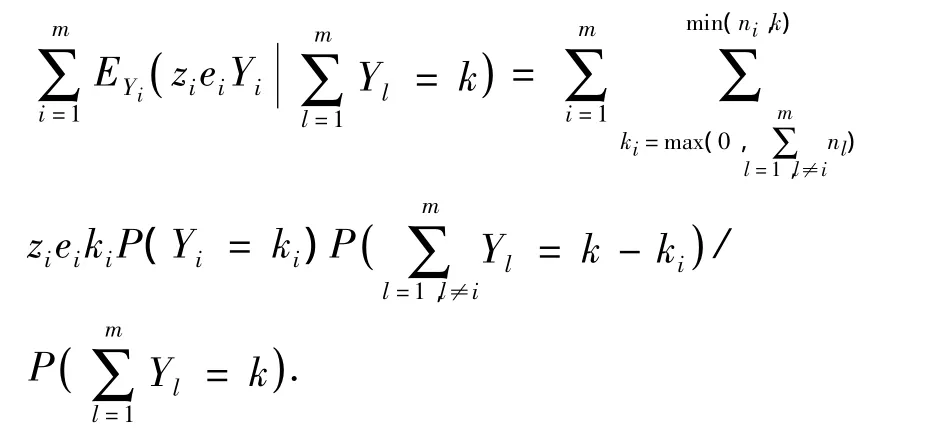
证明 对于供应商i，Yi是供应商i的随机延迟周期，由于Xi，i=1，2，…，m相互独立，则Yi，i=1，2，…，m，相互独立。设ki是Yi的可能取值，ni是Yi的最大可能取值。当时，供应商i延迟周期为的ki概率为

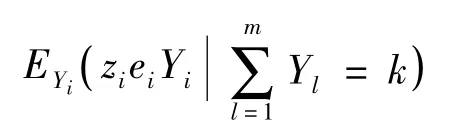
由条件期望的定义[11]可知:

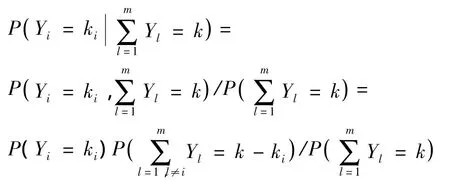
由于Yi，i=1，2，…，m为非负随机变量，且ni是Yi的最大可能取值。因此，当ki＞k或ki＜时，

(1)若ni≤k，则当时，从供应商i订购零部件的平均延迟成本:

(2)若ni＞k，则当时，从供应商i订购零部件的平均延迟成本:

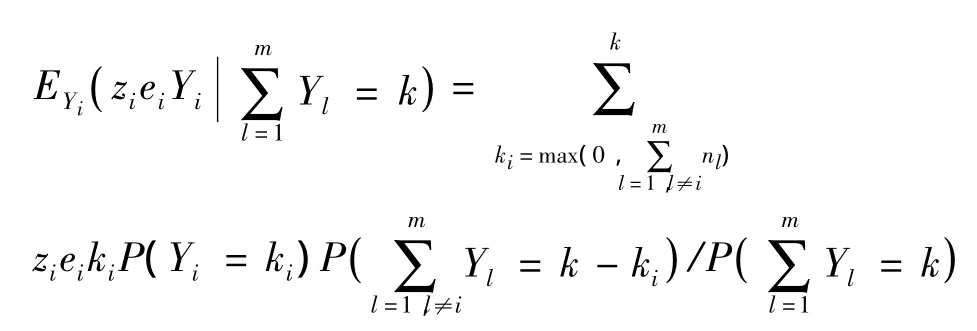
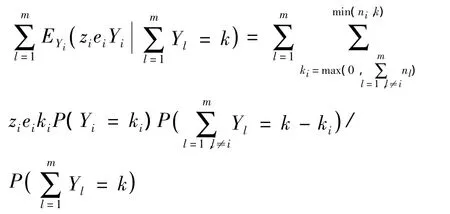
显然，定理2给出了所有供应商的总延迟周期在不同取值情形下相应的延迟成本，这为供应商选择决策中比较不同方案的成本提供了可能。由式(4)可以看出，在计算从供应商订购零部件的平均延迟成本时需要计算，定理1为计算指数分布和的离散化情形奠定了基础。

3 算法

为了计算所有供应商总延迟周期在不同取值情形下的总延迟成本，利用定理1与定理2，我们给出如下算法:

算法

1 对i=1，2，…，m执行:

1.1 对于ki=0，1，…，ni利用指数分布的密度函数计算P(Yi=ki):当ki＜ni时，P(Yi=ki)=P(ki≤Xi＜ki+1)当ki=ni时，P(Yi=ki)=P(ni≤Xi)

1.2 对于j=0，1，…

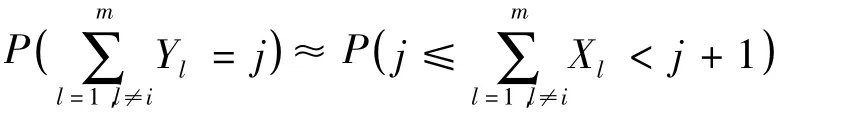
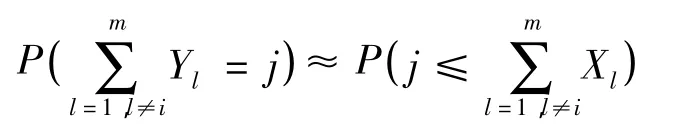
2 对k=0，1，…执行:

2.1 令i=1;Sum=0;

2.2 令ki=max();sum=0.

2.3利用第1步的结果计算

2.4 令ki=ki+1，

如果ki≤ min(ni，k)，返回 2.3 步;

否则，退出循环。

2.5 计算 Sum=Sum+sum.

2.6 令i=i+1，

如果i≤m，返回第2.2 步;

否则，退出循环。

3输出Sum

当所有供应商的延迟随机变量独立同分布时，上述算法可以简化。这是由于对于i=1，2，…，m，Yi同分布也同分布。

[1]SAWIK T.Supplier Selection in Make-to-order Environment with Risks[J].Mathematical and Computer Modelling，2011，53(9-10):1670-1679.

[2]SAWIK T.Selection of supply portfolio under disruption risks[J].Omega，2011，39:194-202.

[3]SAWIK T.Single vs Multiple Objective Supplier Selection in a Make-to-order Environment[J].Omega，2010，38:203-212.

[4]ROCKAFELLAR R T，URYASEV S.Optimization of Conditional Value-at-risk[J].The Journal of Risk，2000，2(3):21-41.

[5]ROCKAFELLAR R T，URYASEV S.Conditional Value-at-risk for General Loss Distributions[J].Journal of Banking and Finance，2002，26(7):1443-1471.

[6]BASNET C，LEUNG M Y.Inventory Lot-sizing with Supplier Selection[J].Computers ＆ Operations Research，2005，32:1-14.

[7]USTUN O，DEMIRTAS E A.An Intergrated Multi-objective Decision Making Process for Multi-period Lot Sizing with Supplier Selection[J].Omega:The International Journal of Management Science，2008，36:509-521.

[8]GHODSYPOUR S H，BRIEN C O.The Total Cost of Logistics in Supplier Selection under Conditions of Multiple Sourcing，Multiple Criteria and Capacity Constraints[J].International Journal of Production Economics，2001，73:15-27.

[9]CHE Z H，WANG H S.Supplier Selection and Supply Quantity Allocation of Common and Non-common Parts with Multiple Criteria under Multiple Products[J].Computers and Industrial Engineering，2008，55:110-133.

[10]方园园，王耀文.基于熵技术的供应商模糊分析评价方法和应用[J].太原科技大学学报，2007，28(3):220-222.

[11]茆诗松，程依明，濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社，2004.