并联式混合动力逻辑门限控制参数智能优化
2012-08-01申爱玲袁文华左青松伏军
申爱玲,袁文华,左青松,伏军
(1.邵阳学院 机械与能源工程系,湖南 邵阳,422000;2.湖南大学 机械与运载工程学院,湖南 长沙,410082)
并联式混合动力汽车是指采用2种或2种以上能量源作为汽车动力装置的汽车,这种多个能量源的特征增加了系统设计的灵活性。在混合动力汽车整车能量管理系统的协调控制下,多个能量源与其他部件相互配合可以进行多种优化组合,形成不同的动力系统驱动模式。但是,由于存在多能量源系统,增加了并联式混合动力汽车对燃油消耗和尾气排放的控制难度。近年的研究表明[1-2]:在多种工作模式下,对多个能量源系统之间的功率与能量的优化匹配研究和有效提高汽车动力性能、降低汽车的燃油消耗、减少尾气排放成为目前混合动力汽车研究领域的热点与难点之一[3-5]。粒子群优化(Particle swarm optimization, PSO)算法是一种基于群体智能的随机优化算法[6-8],其基本思想是通过种群中粒子间的合作与竞争产生的群体智能指导优化搜索,其原理和机制简单,既保持了进化算法深刻的群体智能背景,又具有良好的优化性能。该算法已广泛应用于函数优化、多目标规划、神经网络训练、模糊系统控制等领域。但传统的PSO算法在优化复杂函数时存在许多缺点,如局部搜索能力较弱、搜索精度不高、易陷入局部最优等。利用在有限区域内折叠次数无限的混沌模型来产生混沌变量,并采用自适应混沌模型改变优化变量的搜索空间,不断提高搜索精度的方法可以有效解决粒子群优化易出现的早熟收敛现象,引导粒子快速跳出局部最优难题,为此,本文作者提出一种新的自适应混沌粒子群优化(Adaptive chaos particle swarm optimization,ACPSO)算法。该算法既具有良好的搜索导向,又能够充分利用混沌的遍历性和粒子群算法的多样性,使得算法收敛速度快,搜索能力强。本文采用自适应混沌粒子群优化对并联式混合动力汽车逻辑门限控制策略参数进行优化,建立基于自适应混沌粒子群优化的并联式混合动力汽车优化模型,并对其优化后的参数进行仿真验证,以便为有效提高并联式混合动力汽车性能提供理论和技术支撑。
1 并联式混合动力逻辑门限控制多目标优化模型
1.1 优化参数与取值区间
根据并联式混合动力汽车实际设计要求,结合控制参数对其特性的影响因素,选取并联式混合动力逻辑门限控制策略优化参数为:发动机最大功率Pe-max,发电机最大功率Pm-max,期望电池的荷电状态最高值εcs-hi-soc,期望电池的荷电状态最低值 εcs-lo-soc,电机启动最小汽车速度vcs-electric-launch-spd-lo,电机启动最高汽车速度发动机关闭转矩系数发动机最小转矩系数
1.1.1 发动机最大功率Pe-max
在并联混合动力汽车动力系统中,发动机功率的设计是非常重要的。若发动机的功率取值偏大,则电动汽车运行于低负荷区的可能性就大,从而导致排放不良,且费用较高;若发动机的功率取值偏小,则后备功率就小,为了满足汽车的动力性要求,需要相应功率的电动机以及电池容量与之匹配。为了加快自适应混沌粒子群优化算法的运算速度和优化效率,其发动机最大功率取值区间的上限计算公式为:
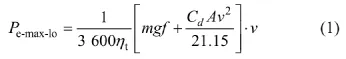
式中:ηt为整车动力传动系效率,ηt=ηgc·ηmc;ηgc为发电机的发电转换效率,%;ηmc为电动机的电能转化为机械能的效率,%;m为汽车质量,kg;f为滚动阻力系数;Cd为空气阻力系数;A为汽车迎风面积,m2;v为汽车在平坦路面匀速行驶的速度,km/h。
根据式(2)对发动机最大功率取值区间的下限进行确定:

式中:Pe-max-hi为发动机最大功率取值区间的下限,kW;α为系数,由于通常情况下发动机燃油消耗的经济区域为发动机满负荷输出功率的60%~80%,本文取a=0.75。
1.1.2 发电机最大功率Pm-max
混合动力系统中电动机的外特性是指在额定转速以下电动机按照恒转矩模式工作,而在额定转速以上按照恒功率模式工作,并且根据整车的控制策略,在车速过低时,关闭发动机而由电动机提供驱动能源,应该满足车辆的爬坡性能;在车辆加速时,电动机提供峰值功率,由此可以根据式(3)和(4)求得发电机最大功率取值区间的上限和下限:
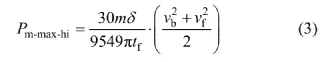
式中:Pm-max-hi为发电机最大功率上限,kW;δ为旋转质量换算系数;tf为加速时间,s;vf为车辆在时间tf内加速所达到的速度,m/s;vb为电机的基速nmb所对应的车速,m/s。
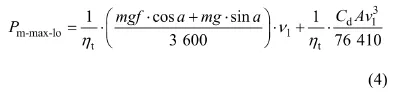
式中:Pm-max-lo为发电机最大功率下限,kW;v1为爬坡时车辆的速度,km/h;a为加速度,m/s2。
为缩小优化参数变化范围与实际设计标准要求[9],并根据并联式混合动力汽车逻辑门限控制策略参数的计算公式与设计经验可以确定并联式混合动力汽车逻辑门限控制策略参数的取值区间为:
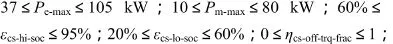

1.2 并联式混合动力逻辑门限控制多目标函数的建立
优化参数的目的是提高燃油经济性、降低污染物(CO,HC和NOx)的排放,则优化目标为:
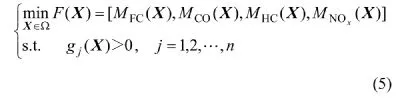
式中:X为本文所选的逻辑门限控制参数的向量;MFC(X)为燃油消耗,L/(100 km)-1;MCO(X)为CO的排放量,g/km;MHC(X)为HC的排放量,g/km;MNOx(X)为NOx的排放量,g/km;gj(X)>0为约束条件,表示电动汽车必须满足所需的最高车速、加速性能和爬坡能力。F(X)为目标函数,具体形式为:
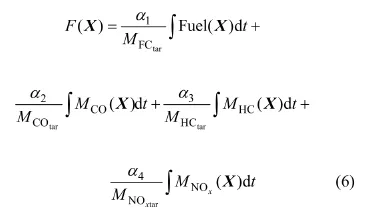
式中:α1,α2,α3和α4为权重影响因子;和为排放设定值。
1.3 基于自适应混沌粒子群优化算法
并联式混合动力逻辑门限控制参数优化中的粒子群控制变量X可表述为:
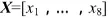
式中:x1为Pe-max;x2为Pm-max;x3为 εcs-hi-soc;x4为vcs-electric-launch-spd-lo;x5为 ηcs-min-trq-frac;x6为vcs-electric-launch-spd-hi;x7为 ηcs-off-trq-frac;x8为 εcs-lo-soc。
将粒子群X中的每组控制变量各分量映射到混沌空间,然后,采用Logistic方程产生混沌序列,其表达式为:
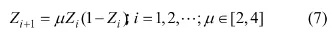
式中:μ为控制参数,当 μ=4时,1≤Z0≤1,系统处于混沌状态。
由于PSO算法本身的局限性使其易陷入局部最优,而混沌在一定范围内具有遍历性、不重复性,因此,在 PSO 算法中引入混沌搜索,以获得全局最优解。自适应混沌粒子群算法的核心思想是:当粒子陷入早熟收敛状态时进行混沌搜索,引导粒子快速跳出局部最优,避免陷入早熟收敛[10-13]。
自适应混沌粒子群算法中,每个粒子对应1个待优化问题的潜在解。粒子Pi有自己的位置和速度,分别表示为向量Xk=(xk1, xk2,…, xkN)和Vk=(vk1, vk2,…,vkN)。其中:Xk对应的目标函数值,称为粒子的适应值fk,度量粒子的优劣程度;Vk决定粒子运动的方向和距离。粒子Pk始终记为自身目前找到的最优解,称为个体极值pbestk;求得整个个体目前找到的最优解,称为全局极值gbest;通过追踪者来更新自己。
PSO算法初始随机生成一群粒子,其迭代求解迭代终止条件为预先确定的最大迭代次数或者达到其优化结果的精度要求。 经过m次迭代,粒子Pk按照Kennedy和Eberhart最早提出的PSO算法即式(8)来更新自己的速度和位置:
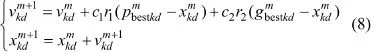
式中:k=1,2,…,K;d=1,2,…,D;学习因子c1和c2为非负常数;r1和r2为0和1之间的随机数;vkdm和xkdm分别为粒子Pk在第m次迭代中第d维的速度和位置,两者均被限制在一定的范围内。
因为gbest是整个粒子群的最优位置,因此,上述PSO算法也被称为全局版PSO。也可以将第k个粒子的邻居们搜索到的最优位置作为g′best,则上述方法又被称为局部版PSO。全局版PSO收敛速度快,但有时会陷入局部最优。局部版PSO收敛速度较慢,但不易陷入局部最优,可以加快搜索速度。
对式( 8)进行如下修改:
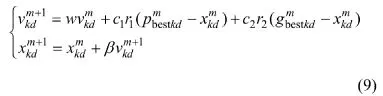
式中:w为惯性因子,为非负数;β为约束因子,控制速度。
粒子群到达局部最优附近时,粒子速度的更新主要由 wvkd来决定。由于固定参数的PSO算法其惯性因子w通常小于1,粒子的速度将会越来越小,甚至停止运动,发生早熟收敛则采用混沌细搜索,选择适应值较大的10%个体进行混沌细搜索,其算法设计步骤如下。
Step 1:混沌初始化粒子群,包括粒子的速度、位置和个体极值pbestk,全局极值gbest。
Step 2:对群体中某一个粒子Pk,执行以下操作:
① 根据式(9)更新 Pk的速度和位置;
② 根据式(10)计算Pk的适应值fk。
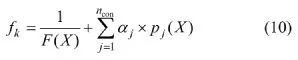
其中:fk为第k个粒子的适应度;j为约束;F(X)为目标函数;aj为正约束值;pj(X)为与第j个约束有关的罚函数;ncon为正整数。
③ 若fk优于pbestk的适应值,则更新pbestk为Pk的当前位置;
④ 若fk优于gbest的适应值,则更新gbest为Pk的当前位置。
Step 3:判断算法的终止条件是否满足,若满足,则转向Step 5;否则,执行Step 4。
Step 4:对较优粒子进行混沌细搜索,根据式( 7)进行迭代产生混沌变量序列为Z=(Z1,Z2,…,Zk),混沌变量搜索区间的缩小表示为:
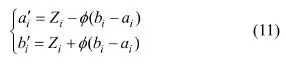
式中:φ为收缩因子,φ∈(0,0.5)。
因此,Zi在新区间[ai′,bi′]上经还原处理后的Yi由下式确定:

将Yi与Zi,n+1的线性组合作为新的混沌变量,用此混沌变量进行搜索。
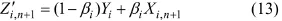
式中:βi为自适应调节系数,0<βi<1。自适应调节系数βi采用如下方法进行自适应确定:

式中:m为整数,根据目标函数而定(本文取为2);K为迭代次数。
Step 5:程序终止判定:若算法符合其终止要求,则输出最优解,并结束其搜索;否则,算法程序继续运行Step 1。
由于自适应混沌粒子群优化本质上并非直线向最优点搜索,所以,不能用搜索次数作为停止条件,只能利用相邻2次目标函数之差的绝对值小于给定值作为终止条件,然后,利用多次寻优结果中最小目标函数值改进参数解空间和终止条件;同时,判断目标函数是否小于最小目标函数值。
2 并联式混合动力逻辑门限控制参数智能优化应用实例
2.1 并联式混合动力逻辑门限策略控制参数优化结果与分析
基于Matlab软件平台,根据上述算法流程编写自适应混沌粒子群优化算法主程序进行优化。为了比较优化效果,分别应用粒子群优化算法PSO和遗传算法GA对所建立的优化问题进行求解,其优化效果如图1所示。
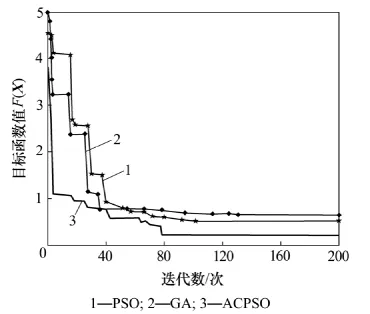
图1 不同优化算法下目标函数值随迭代次数变化曲线Fig.1 Iteration times-objective function value of various optimization algorithms
从图1可以看出:ACPSO算法在开始几代下降速度很快,表明混沌初始化使该算法能从较好的初始值开始寻优,进而加快了搜索速度,自适应惯性权重因子和混沌优化部分局部极值粒子等改进措施使得ACPSO算法收敛速度和精度提高;ACPSO算法在迭代80次左右时非常接近最优解,而PSO算法要迭代到110次才能达到最优解,GA要迭代140次左右才能达到最优解,可见本文提出的自适应混沌粒子群优化算法具有较好的收敛性和稳定性。
以提高燃油经济性、降低污染物CO,HC和NOx排放量为优化目标,利用ACPSO算法对并联式混合动力逻辑门限控制策略参数进行优化,其逻辑门限控制策略参数优化值如表1所示。
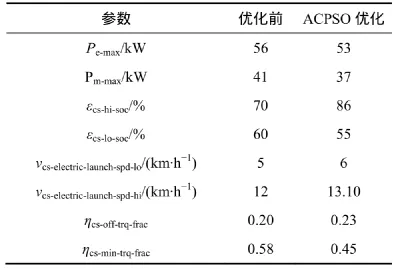
表1 ACPSO优化参数值Table1 Parameter optimization values
2.2 基于自适应混沌粒子群优化算法的并联式混合动力优化模型验证
为验证自适应混沌粒子群优化算法对并联式混合动力逻辑门限控制策略参数优化后的应用效果,采用ADVISOR软件对并联式混合动力汽车进行仿真试验,仿真模型如图2所示。选择城市道路循环UDDS(Urban dynamometer driving schedule)作为试验工况,其循环时间为1 365 s,行驶路程为25 km,最高车速为90.25 km/h,平均车速为30.51 km/h,最大加速度为1.48 m/s2,最大减速度为-1.48 m/s2,行驶期间共计18次停车。整车仿真主要参数如表2所示。
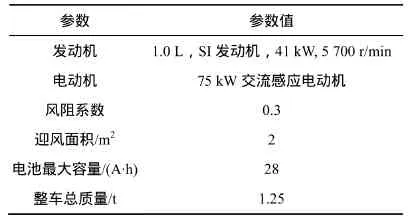
表2 并联式混合动力汽车整车参数Table2 Vehicle parameters of parallel hybrid electric vehicle
将未优化的逻辑门限控制策略参数和在自适应混沌粒子群优化下得到的最佳并联式混合动力逻辑门限控制策略参数分别作为ADVISOR软件仿真的控制参数进行仿真试验,得到的发动机输出转矩和电动机输出转矩分别如图3和图4所示。
从图3可知:优化后的逻辑门限控制能实现发动机运行时工作于转矩范围40~60 N·m内[14],在这一区域内发动机燃油经济性较好。从图4可知:电动机处于辅助驱动状态时提供较小的驱动转矩,电动机处于再生发电状态时能回收大部分能量,这样,蓄电池的电就可以由电动机提供,而不需要消耗燃油为蓄电池充电,因此,采用转矩分配策略取得了较满意的结果。
通过ADVISOR仿真,在UDDC工况下得到不同输入参数下并联式混合动力汽车的动力性能和油耗及排放对比结果,如表3和表4所示。
从表3可知:在满足目标函数F(X)最小的优化策略下,得到并联式混合动力汽车必须满足最小所需的最高车速、加速性能和爬坡能力,即在满足车辆基本动力性的前提下尽可能地减少动力系统部件的功率、体积以及质量以控制汽车的制造成本,验证了于自适应混沌粒子群优化策略的有效性。
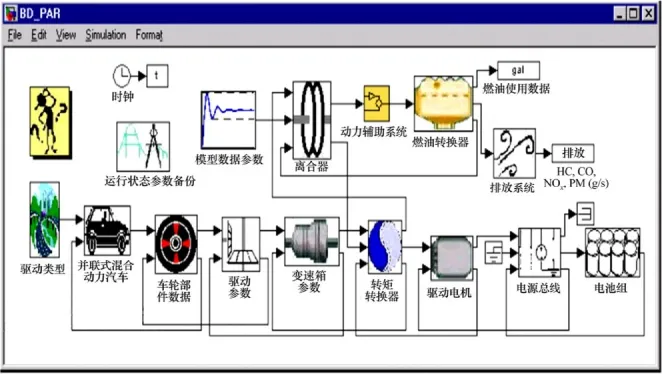
图2 并联式混合动力汽车仿真模型Fig.2 Simulation model of parallel hybrid electric vehicle

图3 UDDS工况下发动机输出转矩Fig.3 Engine output torque under UDDS test conditions
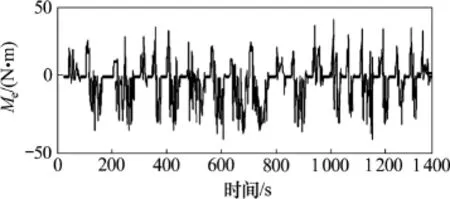
图4 UDDS工况下电动机输出转矩Fig.4 Electric motor output torques under UDDS test conditions
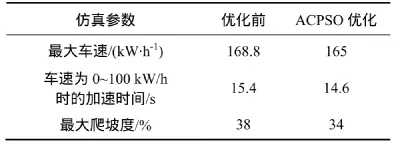
表3 动力性能对比Table3 Comparison of power performance
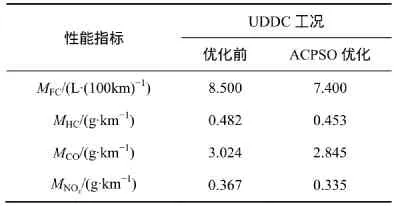
表4 油耗及排放对比Table4 Comparison of fuel consumption and emissions
从表4可知:ACPSO优化后的控制策略明显优于优化前的控制策略;优化后的每100 km油耗为7.400 L,比优化前的每100 km油耗(8.500 L)至少降低了12%,且HC排放量降低了6%,CO排放量降低了5%,NOx排放量降低了8%,取得了较好的优化效果。
3 结论
(1)自适应混沌粒子群优化算法具有较快的收敛速度和较高的收敛精度,能有效避免早熟收敛问题。
(2)ACPSO优化后的控制策略明显优于优化前的控制策略。从UDDC典型工况下的仿真结果可以看出:优化后的每100 km油耗为7.4 L,比优化前的每100 km油耗至少降低了12%,且HC排放量降低了6%,CO排放量降低了5%,NOx排放量降低了8%,取得了较好的优化效果。
[1]Morteza M G, Poursamad A, Ghalichi B.Application of genetic algorithm for optimization of control strategy in parallel hybrid electric vehicles[J].Journal of the Franklin Institute, 2006,343(4/5): 420-435.
[2]吴光强, 陈慧勇.基于遗传算法的混合动力汽车参数多目标优化[J].汽车工程, 2009, 31(1): 60-64.WU Guang-qiang, CHEN Hui-yong.Multi-objective optimization of HEV parameters based on genetic algorithm[J].Automotive Engineering, 2009, 31(1): 60-64.
[3]Ayad M Y, Becherif M, Henni A.Vehicle hybridization with fuel cell, supercapacitors and batteries by sliding mode control[J].Renewable Energy, 2011, 36(10): 2627-2634.
[4]Poursamad A, Montazeri M.Design of genetic-fuzzy control strategy for parallel hybrid electric vehicles[J].Control Engineering Practice, 2008, 16(7): 861-873.
[5]SUN Hui, YANG Li-fu, JING Jun-qing.Control strategy of hydraulic/electric synergy system in heavy hybrid vehicles[J].Energy Conversion and Management, 2011, 52(1): 668-674.
[6]TANG Xian-lun, LING Zhuang, CHANG Jiang.Prediction of silicon content in hot metal using support vector regression based on chaos particle swarm optimization[J].Expert Systems with Applications, 2009, 36(9): 11853-11857.
[7]Alatas B, Akin E, Bedri O A.Chaos embedded particle swarm optimization algorithms[J].Solitons & Fractals, 2009, 40(4):1715-1734.
[8]GE Hong-wei, LIANG Yan-chun, Marchese M.A modified particle swarm optimization-based dynamic recurrent neuralnetwork for identifying and controlling nonlinear systems[J].Computers & Structures, 2007, 85(22): 1611-1622.
[9]陈祥丰.混合动力SUV总成参数匹配与优化[D].武汉: 武汉理工大学汽车工程学院, 2010: 59-62.CHEN Xiang-feng.Parameter matching and optimization of assembly for hybrid SUV[D].Wuhan: Wuhan University of Technology.Automotive Engineering Institute, 2010: 59-62.
[10]杨海东, 鄂加强.自适应变尺度混沌免疫优化算法及其应用[J].控制理论与应用, 2009, 26(10): 1069-1074.YANG Hai-dong, E Jia-qiang.Intrusion detection of mobile Ad Hoc networks based on collateral chaos artificial immune clustering algorithm[J].Control Theory and Applications, 2009,26(10): 1069-1074.
[11]E Jia-qiang, WANG Chun-hua, WANG Yao-nan.A new adaptive mutative scale chaos optimization algorithm and its application[J].Journal of Control Theory and Applications, 2007,6(2): 141-145.
[12]赵志刚, 常成.自适应混沌粒子群优化算法[J].计算机工程,2011, 37(15): 128-130.ZHAO Zhi-gang, CHANG Cheng.Adaptive chaos particle swarm optimization algorithm[J].Computer Engineering, 2011,37(15): 128-130.
[13]谢常清.无芯中频感应电炉无磁性期电热效率智能优化[J].工业炉, 2008, 30(2): 29-32.XIE Chang-qing.Effectiveness analysis of intermediate frequency coreless induction furnace in the nonmagnetic process[J].Industrial Furnace, 2008, 30(2): 29-32.
[14]钱立军, 袭著永, 赵韩.基于模糊神经网络的混合动力汽车控制策略仿真[J].系统仿真学报, 2006, 18(5): 1384-1387.QIAN Li-jun, XI Zhu-yong, ZHAO Han.Simulation of hybrid electric vehicle control strategy based on fuzzy neural network[J].Journal of System Simulation, 2006, 18(5): 1384-1387.
