基于公平视角的企业集团内部资金配置激励模型

高永如

（1.河海大学 商学院，南京 210098；2.银城地产集团股份有限公司,南京 210036）

0 引言

资源分配问题在经济、管理等领域有着广泛的应用，其经典的数学模型是典型的线性规划问题，约束条件中的资源拥有量是一定的。而本文所考虑的企业集团内部资金配置问题中的资金则是在允许的一定范围内变化的，而且，资金供应给集团不同分部可以是单个项目或多项目共同使用，集团总部CEO或分部经理需要通过资金的优化配置以发挥其最大效益。一方面，集团总部CEO通过对集团各分部实施合理的资金配置去实现集团利益最大化目标；另一方面，分部经理通过对各项目优化配置发挥单位资金投入的最大产出。

企业集团总部根据各分部现有项目的实际资金需求以及未来拟投资项目的资金计划，并参考各分部过往项目投资绩效以及分部经理的投资管理水平，综合权衡后下达各个分部的资金计划。各分部按照集团给定的资金计划，在各个项目之间进行合理分配。这样，企业各分部投资项目的确立实际上相当于资源（这里主要指资金投入）的分配。如何将有限的资源在不同分部以及不同分部的项目之间进行合理的分配，以便企业集团在总体上得到最优或满意的效果，即是本文所研究的主要问题。

1 模型假定

企业集团资金分配是一个非常复杂的现实问题。本文将其描述成为一个集团总部、分部、分部的投资项目三个级别的两层资金分配决策问题。这里所考虑的集团总部只有一个，分部以及分部的投资项目均有多个。假设集团总部资金总量为T，需要在I个分部之间进行分配。第i个分部对应有Ki个投资项目，而分部i的第k个投资计划有Jik个项目可供选择。决策主要发生在如下两层：集团总部在各个分部之间分配有限的资金；各个分部根据集团总部所分配的资源在各个投资机会中选择合适的实施项目。本文假定每个分部至少有一个项目要实施，否则表明该分部不参加此次资金分配，从而不予考虑。

集团总部目标是在满足资金总量限制的前提下，在各个分部之间进行最佳的资金分配，在各个分部取得最大效益的同时，还要使得资金分配比较公平（假定每个分部的资金需求都是合理的，集团总部应该兼顾各个分部的资金需求，而不是将资金集中分配给某些分部。倘若资金分配不公平，则会打击个别分部的积极性，因而对集团的整体发展也会造成一定的影响。）

公平性的概念在经济学、操作系统及通信网络中各有不同的描述。生活中，人们通常认为平均的就是公平的。但是“公平”实际上是一个很复杂的概念，也许从某一个角度认为一个分配是公平的，但是在另一个角度分析这个分配却很可能是不公平的。例如，在企业资金配置中，我们可以对各分部提供相同的资金，那么从平均分配的角度看这是公平的；但是，我们知道每个分部所产生的效益是有很大的差异的，这将导致各个分部的业绩大不相同，这时从各个分部福利待遇来看，这种资源分配方式就是很不公平的。也就是说，“公平”是有条件的，在我们分析不同的问题时，我们需要定义适合的公平性的概念及相应的衡量标准。

在进行企业集团内部资金分配时，如果企业总部给各个分部提供相等的资金利用机会，如Round-Robin算法，将使得效益较好的分部获得较多的资金利用机会，而对于效益较差的分部则获得较少的资金利用机会；如果企业总部希望各个分部获得相等的资金产出效益，则要给效益较差的分部提供更多的资金利用机会。显然，上述两种方法都存在着不公平的问题，那么我们就需要设定一种标准来衡量用户间的资源分配，使其具有一定的公平性。

近年来，关于效用的公平性研究研究受到很多专家学者的重视，由于它能够根据不同的应用给出相适应的公平性概念，因此该种方法用来反映公平性具有一定的优点。对于公平性的特征，有很多学者利用效用来作为评价标准，而基于上述内容，本文将运用边际效用来对资金公平性进行评判，下面对基于边际效用的公平性概念进行详细的说明。

定义 令上凸函数Uk(xk)为对分部k所分配资金的实际效用函数，则分部k所分配资金的边际效用函数为如果某种分配向量是可行的分配空间中一个基于边际效用公平的分配，其中n为集团分部数量，那么使得下列公式取得最大值：

资金利用的边际效益是指在其他要素都不变的情况下，在当前资金需求的基础上每增加一单位的资金，所增加的产值。

集团分部以及各个分部的投资项目对资金的需求可分解为启动资金和激励资金两个部分，前者是用于维系企业生存的必须资金，后者则是集团总部为了调动各个分部的工作积极性给与的激励措施资金，因此，企业集团总部的资金一共分为两个部分：启动资金Q和激励资金W。企业集团总部的激励资金W在不同分部i进行分配，可以有不同的组合方案Wi，产生不同的经济效益Si和据此，企业集团总部激励资金分配的定界问题可描述为（图1）：

图1 激励资金利用边际效益

假设集团各个分部有各自的启动资金，对各个分部按照各自的启动资金利用边际效益自大到小进行编号：i=1,2,…,I,共I个分部；同时，假设第i分部的边际效益为fi，初始的资金可用量Q0i，对应的初始边际效益为y0i=fi(Q0i)，而企业集团总的激励资金为W，所对应的分配后的均衡边际效益为y。显然，第j分部初始边际效益y0j对应第i分部总资金消费量，其中，i≤j,i,j=1,2,…I，即这里第i分部总资金消费量为Qi=Q0i+Wi，包括第i分部初始资金拥有量Q0i和从企业总部获得的激励资金Wi。问题变为求第i分部的激励资金获得量Wi，以使得企业集团总部的资金利用经济效益S最大。

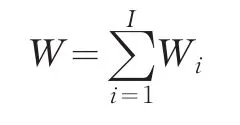
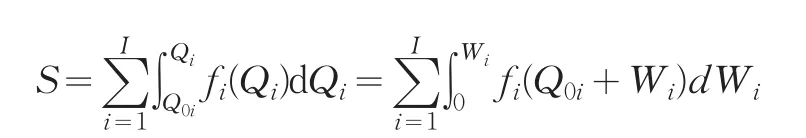
其中，资金利用边际效益fi(Qi)可以由测算数据和二次函数回归获得。

用拉格朗日条件极值法求解上述式子，则有如下求解过程

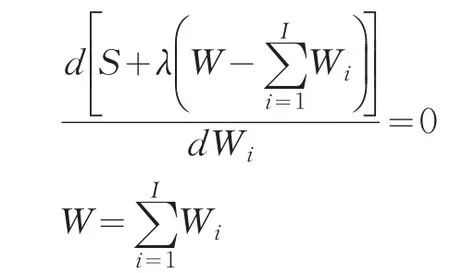
并且满足递减函数条件

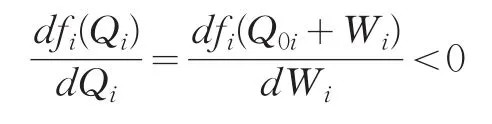
即

以上式子含义为：为使企业集团资金总效益S最大，资金首先应该分配给边际效益最大的分部1，直至边际效益从y01降低到y02。此后资金应该在分部1和分部2进行同时分配，以保持各自资金消费量对应的边际效益相等，否则，倘若只在某些分部，如在分部1连续分配资金，这必将导致分部1所对应的边际效益小于分部2的边际效益；这时若考虑在分部2分配资金则会产生相对较大的经济效益。以此类推，在多个分部之间进行资金分配时，只有保证各个分部资金利用的边际效益均衡，才能使得企业集团总部的资金在所有分部所产生的总的经济效益最大。因此，企业集团资金配置的边际效益均衡原理可叙述为：当各个分部的资金利用的边际效益均衡时，整个企业的资金利用总体经济效益最大。

2 完全激励分配

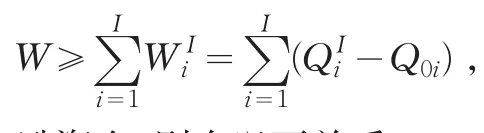
假设企业集团动用的激励资金W足够多，即则所有的分部都能够得到激励资金，则有以下关系：

上式计算可以得到y，由此得到对应值Qi=gi(y)，从而最终得到各个分部的激励资金Wi=Qi-Q0i。这样求得的解相对来说比较简单，考虑到拟合精度和求解过程之间的平衡，根据边际效益理论和以往的研究，可以运用二次函数拟合得到gi：

有

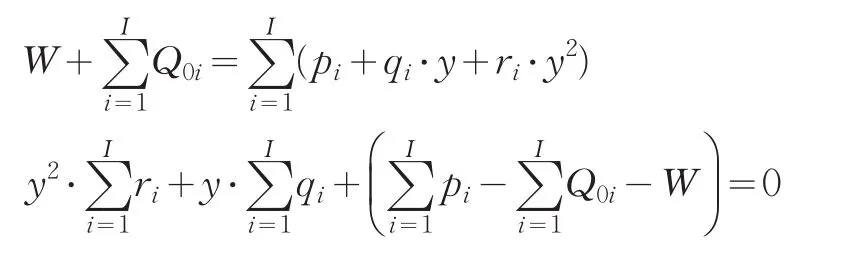
由二次函数的求根公式算得：

上式中分子正负号的选择可通过简单的推算得到。各个分部激励资金最优分配应为：

各个分部资金利用效益分别为：

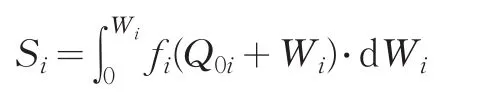
企业集团总部资金利用最大效益为：

其中各分部资金利用边际效益可以通过二次函数拟合得到。

各个分部将获得的启动资金和激励资金合理分配给各自的投资项目则运用同样的边际效益均衡原理获得分配方案。

3 不完全激励分配

当激励资金有限的情况下，个别的分部则不参加分配，只有J个分部参加分配（J＜I），分配模型与上述情况相同，将I替换为J即可。

不完全激励分配的关键问题是已知W求J。首先，通过列出第J分部的初始边际效益所对应的第i分部总的资金消费量其次，计算J个分部总的激励资金最后列出表示与第j分部初始资金Q0j相应的边际效益y0j所对应的激励资金。而对于不同的激励资金W，采用如下的方式进行选择

采用上式所求的J即为所求。

对于本文所讨论的企业集团来说，其各个分部的资金可以通过上述方法进行分配，而且各个分部的投资项目资金也可以采取同样的方法去分配。这样就能够保证整个企业集团资金消费的经济效益最大。

4 结论

企业集团内部资金配置问题一直是倍受企业界所关注的一个问题，这将直接关系到集团各个分部能力的培养以及经济效益的提升。在保证集团正常发展的前提下，在企业发展的市场经济体制中，企业资金的利用应当追求经济效益最大化。为此，本文论证提出了企业资金配置的边际效益均衡理论：当企业各个分部的资金利用的边际效益均衡时，整个企业的资金利用经济效益达到最大。而无论激励资金充足与否，这都是企业所采取的为了提高企业人员工作积极性以提高企业效益的一种激励机制。

[1]汪寿阳.一个资源分配问题的主从对策模型[J].中科院研究生院学报，1992,(9).

[2]杜刚,顾培亮.资源分配问题的层次激励模型[J].管理工程学报，1997,(6).

[3]石永恒.资源分配中引导下级汇报真实信息的激励策略[J].系统工程理论与实践，1994,(2).