基于求解校验序列的(n,1,m)卷积码盲识别

刘建成 杨晓静

(解放军电子工程学院 合肥 230037)

1 引言

在数字通信中，信道编码可以提高信息传输的可靠性，保证通信质量。目前信道编码主要包括线性分组码、卷积码、LDPC码和Turbo码等。卷积码具有纠错能力强和编译简单等优点已广泛应用于卫星系统测控链路、深空探测系统和第3代移动通信系统等，这也使得卷积码识别成为了信息对抗和智能移动通信 AMC(自适应调制编码)技术中实现信息恢复所亟需解决的问题。目前，国外针对信道编码识别研究的公开文献资料相对较少，国内对线性分组码的研究方法主要有文献[1,2]中的秩函数求解、码根统计等；对卷积码识别主要有文献[3]中的基于快速双合冲算法、文献[4]中的欧几里德算法、文献[5,6]中的构建分析矩阵法和文献[7]中的Walsh-Hadamard变换法。欧几里德算法和基于快速合冲算法计算复杂度低、所需数据量小，但只适于无记忆的(2,1,m)卷积码码字序列识别；构建分析矩阵法只对(n,1,m)卷积码和系统卷积码进行了相关的识别分析，且所需数据量非常巨大，在不知子码长度n的情况下一般需要几万比特；Walsh-Hadamard变换法具有较好的容错性能，同时需要参数n、码字起始位置等先验条件和巨大的数据存储空间。可见，现有的卷积码识别方法一般具有应用范围受限、数据利用率低和所需先验条件较多等不足。

(n,1,m)卷积码具有良好的纠错性能，是卫星通信、深空探测等常用的低码率信道编码方式[8]。本文针对该类卷积码提出了一种新的盲识别方法，该方法计算复杂度较低，能够在参数n和码字起始位置均未知的情况下有效完成识别。

2 (n,1,m)卷积码识别问题的描述

本文讨论卷积码是建立在二元域F2上，卷积码是把信源输出的信息序列，以k个码元分为一组，通过编码器输出长为n(n＞k)的一组码字，该码组的n-k个校验元不仅与本组的信息元相关，而且还与先前的m组信息元有关。因此，卷积码一般表示为：(n,k,m)，称k为信息子组长度，n为子码长度，m为编码记忆长度，n(m+ 1 )为卷积码的约束长度[9]。现只讨论k=1的卷积码。

2.1 (n,1,m)卷积码

设I和C分别为(n,1,m)卷积码的信息序列和码字序列，在环F2[x]上二者可以表示为

定义1[9](n,1,m)卷积码的生成多项式矩阵G(x)定义为

则I(x)和C(x)之间满足如下关系：

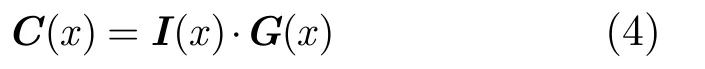
定义2[9]与线性分组码相似，对于卷积码定义校验多项式矩阵，设G(x)是(n,1,m)卷积码的生成多项式矩阵，H(x)为(n-1)×n的多项式矩阵，若满足

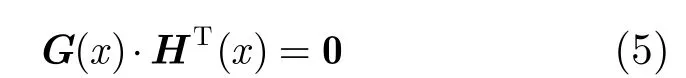
称H(x)为(n,1,m)卷积码的校验多项式矩阵(满足式(5)的H(x)不唯一，T表示矩阵转置)。

由式(3)和式(5)可知

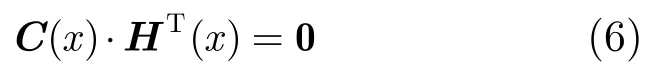
现(n,1,m)卷积码的盲识别问题可转化为求解式(5)和式(6)，本文将通过构建数据利用率高的矩阵识别模型，引入校验序列解决该识别问题。

2.2 识别问题的描述

现将卷积码的编码过程由F2[x]引申至F2上，即由标量矩阵表示，以便由截获或接收到的0, 1序列建立识别模型。

定义3[9](n,1,m)卷积码码字序列C定义为

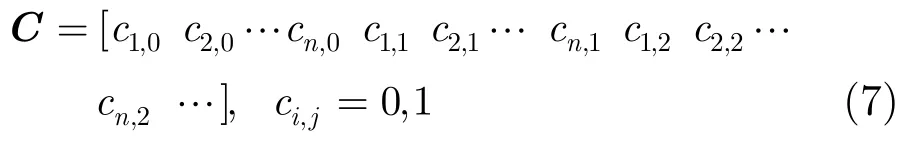
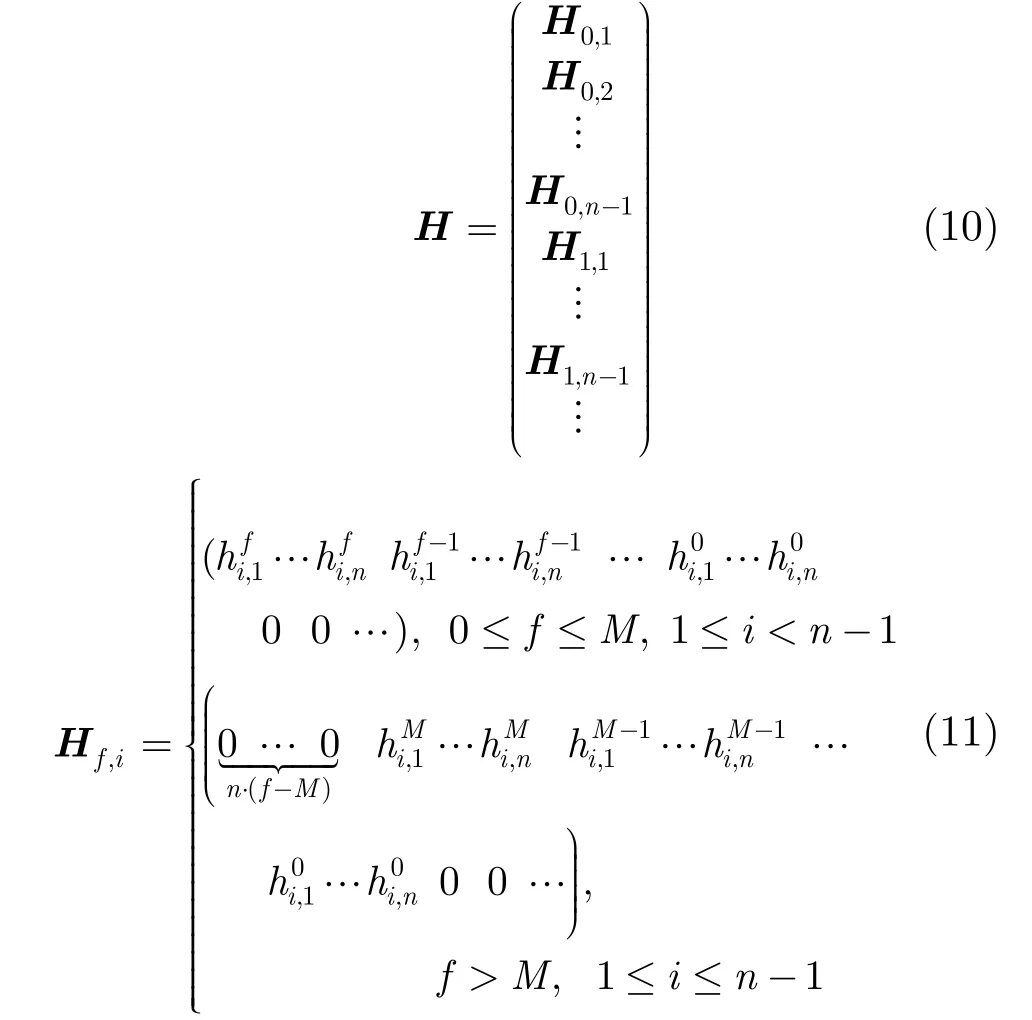
定义4[9]校验矩阵H定义为

其中ht为(n-1)×n的矩阵(0≤t≤M,M等于H(x)中元素的最高幂次的值)，可表示为

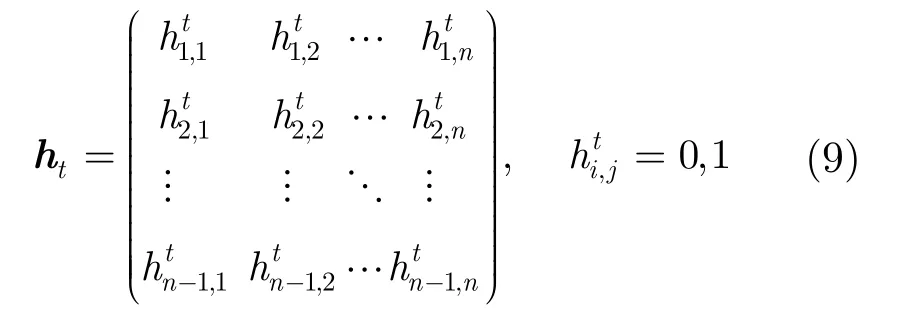
所以，校验矩阵H可看作是(n- 1 )×n(M+ 1 )维矩阵(hMhM-1…h0)的移位，可以表示为

码字序列C和校验矩阵H满足关系式[9]

由于校验矩阵H的不唯一性，故对其求解较为困难。现引入校验序列H'，能容易地由后续内容中建立的矩阵模型求解得出，进而由多个H'构造出校验多项式矩阵H(x)，并由式(5)推导出生成多项式矩阵G(x)。

定义5(n,1,m)卷积码校验序列H'定义为：H'为F2上半无限长行向量

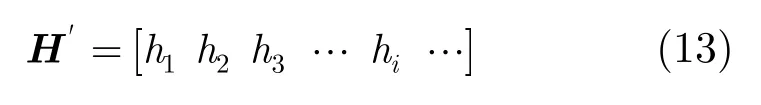
对于(n,1,m)卷积码任意输出的编码序列C，若满足

则称H'为(n,1,m)卷积码的校验序列。

可见，校验矩阵H的各行Hf,i均为校验序列，式(12)可表示为

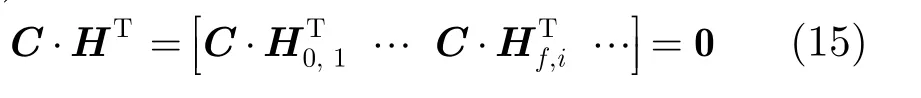
表示成二元齐次线性方程组的形式为

由已知的码字序列C根据式(16)构造求解校验序列H'的方程系数，如式(17)所示，N为[n(M+ 1 ) + 1 ]×n(M+ 1 )维的矩阵，系数矩阵的列数n(M+ 1 )要大于(n,1,m)卷积码的约束长度。由于译码复杂度的限制，卷积码约束长度通常情况下不大于48[10]，构建矩阵N时n(M+ 1 )取值为48即可。

该系数矩阵N即为识别所需的矩阵模型，由其可估计出某一校验序列H'，进而推导出生成多项式矩阵。为方便表示，令L=n(M+ 1 ),L+ 1 =n(M+ 1 ) + 1。

3 识别方法

根据以上建立的识别模型，本节提出了校验序列H'的识别算法和基于H'的生成多项式矩阵G(x)求解方法。针对(n,1,m)卷积码的该识别方法同文献[5]中的方法相比，有效地降低了所需数据量和计算复杂度。

3.1 校验序列H'的识别方法

识别模型的建立和求解中要解决两个问题，如何预知参数(子码长度)n和确定码字起始位置即ci,j中j的数值。通过系数矩阵N的秩可判断估计的n是否正确，进而可以通过化简后的矩阵N'确定码字起始位置，具体算法步骤如下：

(1)设系数矩阵维数(L+1)×L,L=48。

(2)假设参数n依次取5,6,7和 8(实际应用中n不会超过8[5])。因为6是3的倍数，8是2和4的倍数，当估值不准确时只是码字序列多移位整数个子码长，故构建的矩阵N每一行仍满足式(16)。

(3)根据步骤(2)中n的值由已知码字序列C构造系数矩阵N，所需数据量为：(n·49 + 4 8) bit，当n=8时所需数据量最多，为440 bit小于500 bit。

(4)把N化成行最简形N'，计算出N的秩K，判断K是否等于列数L，若等于则表明式(16)只有全0解，N'除最后一行外为单位阵，此时返回步骤(2)改变n的取值；若小于L则表明具有非0解，化简后的矩阵即为要分析的结果，执行步骤(5)。

(5)秩K不等于列数L时，矩阵化简结果如下[5,6]：

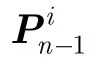
3.2 生成多项式的求解

由上一节可识别出卷积码的参数n和若干个(记为r个)校验序列H'的部分序列，现介绍由识别出的r个部分序列推导出生成多项式矩阵方法的具体步骤：

(3)将方程组式(19)转化为F2上的方程组，利用高斯消元法求解。方程组求解过程中可能存在q(q≥1)组解，由q组解中幂次最小的一组构成生成多项式矩阵G(x)，完成识别。

3.3 计算复杂度分析

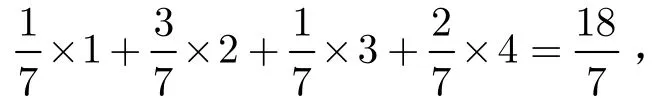
4 仿真实验与容错性分析

本节以常用的(3,1,5)卷积码和(4,1,5)卷积码为例，对该识别方法的有效性进行了验证，同时在蒙特卡洛仿真实验的基础上分析了该识别方法的容错性能，即在码字序列含有误码情况下能够正确识别的能力。

4.1 实例仿真

例1(3,1,5)卷积码的生成多项式矩阵用八进制数分别表示为[11]：G(47 53 75)，即

下面是该卷积码非码字同步的 500 bit编码数据：1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 0 1 0 1 … 0 0 1 1 0 1 0 1 1 1 1 0 0 1 0 1 1 1 0 1。按照2.1节和2.2节的方法建立校验序列识别模型N，估计参数n= 6 时，矩阵模型化简后的N'形式如图1所示。

图1 矩阵模型化简结果

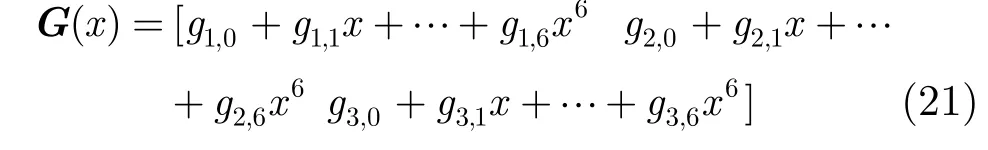
由3.1节推导生成多项式矩阵方法的步骤(2)建立F2上的齐次线性方程组A·GT=0，其中G=[g1,0g1,1…g1,6g2,0g2,1…g2,6g3,0g3,1…g3,6],A为F2上22×21维矩阵，方程组如式(22)所示。

利用消元法求解方程组A·GT=0得解为：G1=[1 0 0 1 1 1 0 1 0 1 0 1 1 0 1 1 1 1 0 1 0],G2=[0 1 0 0 1 1 1 0 1 0 1 0 1 1 0 1 1 1 1 0 1]。可见G2只是G1的移位，所以识别出该码字序列为(3,1,5)卷积码编码序列，生成多项式矩阵为： [1 +x3+x4+x51+x2+x4+x51 +x+x2+x3+x5]，与式(20)相同，识别准确有效。

例2(4,1,5)卷积码的生成多项式矩阵用八进制数分别表示为[11]：G(53 67 71 75)，即

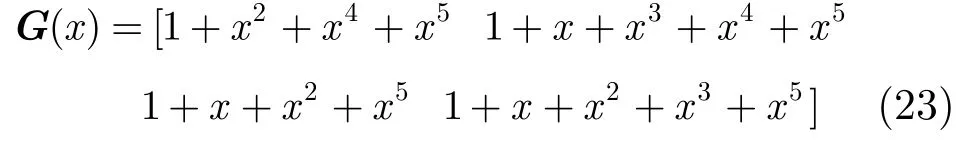
4.2 容错性能分析

在假设子码长度n估值准确情况下，分析该识别方法的容错性能，即能够正确识别不同误码率的码字序列的概率。以4.1节中的(3,1,5)和(4,1,5)卷积码为例，通过蒙特卡洛仿真实验统计正确识别的次数。每次仿真实验从10000 bit的码字序列中随机选取连续的500 bit进行识别，识别概率如图2所示。由图可见，随着子码长度n的增大识别概率有明显的下降，这是因为n的增大增加了约束长度，使长度为n(m+ 1 )的序列含有错误码元的可能性增加；但在误码率高达 1 0-2时，对以上两种卷积码的成功识别率仍可以达到90%以上，所以该方法具有较好的容错性能和较高的实际应用价值。

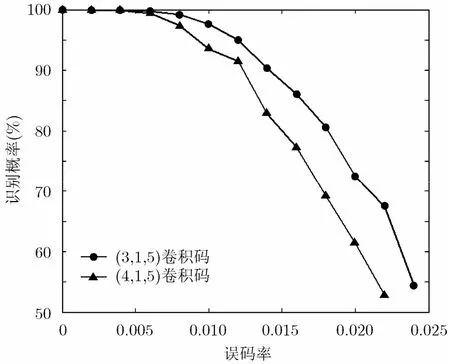
图2 两种卷积码的识别概率

5 结论

本文通过改进的分析矩阵构造方法，在仅需不到500 bit数据量的情况下能够识别出所有(n,1,m)卷积码的子码长度n、码字起始位置和校验序列H'，在对记忆长度进行估计的基础上由校验序列H'的部分序列构造了生成多项式矩阵G(x)的识别方程组，进而利用高斯消元法求解该方程组，准确有效地完成了(n,1,m)卷积码的识别。该识别方法不需任何先验条件，数据利用率高，克服了卷积码现有识别方法的不足，同时具有较好的容错性能，在卫星通信、深空探测及航天控制的通信体制识别、智能通信及信息恢复等领域都有重要应用意义。

[1]闻年成, 杨晓静, 白或. 一种新的 RS码识别方法[J]. 电子信息对抗技术, 2011, 26(2): 36-40.

Wen Nian-cheng, Yang Xiao-jing, and Bai Yu. A new recognition method of RS codes[J].Electronic Information Warfare Technology, 2011, 26(2): 36-40.

[2]闻年成, 杨晓静. 采用秩统计和码根特征的二进制循环码盲识别方法[J]. 电子信息对抗技术, 2010, 25(6): 26-29.

Wen Nian-cheng and Yang Xiao-jing. Blind recognition of cyclic codes based on rank statistic and codes roots characteristic [J].Electronic Information Warfare Technology,2010, 25(6): 26-29.

[3]邹艳, 陆佩忠. 关键方程的新推广[J]. 计算机学报, 2006,29(5): 711-718.

Zou Yan and Lu Pei-zhong. A new generalization of key equation[J].Journal of Computers, 2006, 29(5): 711-718.

[4]Wang Feng-hua and Huang Zhi-tao. A method for blind recognition of convolution code based on Euclidean algorithm[C]. IEEE International Conference on Wireless Communications, Shanghai: IEEE Press, 2007: 1414-1417.

[5]薛国庆, 常逢佳, 柳卫平, 等. 1/n卷积码盲识别[J]. 无线通信技术, 2009, 38(3): 38-42.

Xue Guo-qing, Chang Feng-jia, Liu Wei-ping,et al.. Blind identification of 1/nconvolutional codes[J].Wireless Communication Technology, 2009, 38(3): 38-42.

[6]薛国庆, 李易, 柳卫平. 系统卷积码盲识别[J]. 信息安全与通信保密, 2009, 54(2): 57-60.

Xue Guo-qing, Li Yi, and Liu Wei-ping. Blind identification of system convolutional codes[J].Information Security and Communications Privacy, 2009, 54(2): 57-60.

[7]刘健, 王晓君, 周希元. 基于Walsh-Hadamard变换的卷积码盲识别[J]. 电子与信息学报, 2010, 32(4): 884-888.

Liu Jian, Wang Xiao-jun, and Zhou Xi-yuan. Blind recognition of convolutional coding based on Walsh-Hadamard transform[J].JournalofElectronics&Information Technology, 2010, 32(4): 884-888.

[8]CCSDS/131. 0-B-1-2003, CCSDS Recommendation for TM Synchronization and Channel Coding[S]. Washington:CCSDS Secretariat, 2003.

[9]赵晓群. 现代编码理论[M]. 武汉: 华中科技大学出版社, 2008:154-189.

[10]陈占计. (2,1,4)卷积码的逻辑代数译码方法研究[D]. [硕士论文], 四川大学, 2006.

[11]Katsiotis A, Rizomiliotis P, and Kalouptsidis N. New constructions of high-performance low-complexity convolutional codes[J].IEEETransactionson Communications, 2010, 58(7): 1950-1961.