分布式视频编码中拉普拉斯-柯西混合分布相关噪声模型研究
2012-07-25杨春玲谢小兰
杨春玲 谢小兰
(华南理工大学电子与信息学院 广州 510640)
1 引言
分布式视频编码(Distribution Video Coding,DVC)是建立在 Slepian-Wolf 理论[1]和 Wyner-Ziv(WZ)理论[2]基础上的一种新型的视频编码框架。与传统的视频编码(MPEG-x, H.26x等) 相比,这种视频编码结构编码简单、解码复杂,适合应用于计算能力和内存容量都受限的无线视频终端。
基于 Turbo码的 Discrete Cosine Transform(DCT)域的Wyner-Ziv编码系统TDWZ[3]是当前最典型有效的 DVC系统之一,本文的研究基于TDWZ。
在分布式视频编码中,原始WZ帧与相应边信息间相关噪声模型的准确度对编码效率有很大影响,相关噪声模型越准确,Turbo码成功解码需要的校验位就越少,一方面降低了码率,提高了压缩效率;另一方面,减少了Turbo码解码的计算量。所以,解码端相关噪声的准确建模是分布式视频编码的一个关键技术。
现有的 DVC系统一般采用拉普拉斯分布来描述原始WZ帧和边信息之间的噪声关系,近年来许多研究者对相关噪声模型的研究主要在于如何获得更精确的拉普拉斯参数[4,5]。文献[4]利用残差置信度,提出了子带级、系数级两种不同级别的拉普拉斯参数估计算法。文献[5]利用已经成功解码的部分 WZ帧子带来估计更精确的拉普拉斯参数。文献[6]提出利用拉普拉斯概率密度函数的加权和(利用相应的统计运动矢量场的概率作为权重)对相关噪声进行建模。子带级的拉普拉斯分布模型由于在计算复杂度和精确度上具有良好的折中得到了广泛认可。
本文通过研究发现DVC系统中的DCT残差系数统计分布不完全符合拉普拉斯分布这个假设,而是具有更尖的峰值特性和更长的尾部,为适应残差系数的这两个特性,本文提出拉普拉斯-柯西混合分布(LCMD)模型对TDWZ中的相关噪声进行建模。该混合模型用改进参数的拉普拉斯分布来描述小残差系数的分布,而用柯西分布来描述大残差系数的分布。同时,本文创新性地提出一种简单有效的柯西分布参数估计方法和更精确的拉普拉斯分布参数估计法。
2 TDWZ中DCT残差系数特性分析
本节首先分离线和在线两种情况介绍最典型的子带级拉普拉斯噪声分布模型,然后深入分析TDWZ中的DCT残差系数特性。
2.1 相关噪声概率分布模型
在TDWZ中,原始WZ帧信息与边信息之间的统计特性通常用子带级的拉普拉斯分布来描述,即每一帧的每一子带的残差系数对应一个不同的拉普拉斯参数。
(1)离线的子带级相关噪声模型 文献[4]所提出的离线(理想)的相关噪声模型是假设在解码端可以准确知道原始WZ帧信息,并利用原始WZ帧和边信息的差值作为残差样本来进行拉普拉斯参数估计。其具体步骤如下:
步骤 1 通过式(1)计算WZ和SI 的残差帧:


步骤 3 子带bk中残差系数的分布用参数为αbk的拉普拉斯概率密度函数描述:


(2)在线子带级相关噪声模型 与采用式(1)来估计拉普拉斯噪声模型不同,文献[4]所提出的在线(实际)的相关噪声模型是利用前后两个关键帧之间的运动补偿残差RME来估计的。
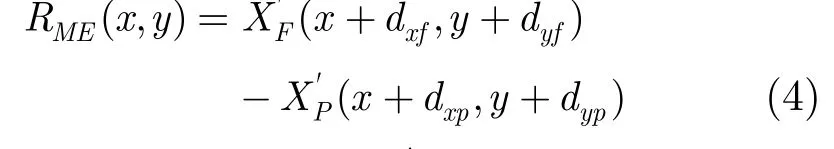
2.2 DCT残差系数特性分析
在分布式视频压缩中,如果残差系数的绝对值比较小,说明此位置的边信息与对应位置的原始WZ帧较相似,因此该位置的边信息置信度较高。拉普拉斯参数本质上是对边信息置信度的一个描述,参数越大,说明边信息置信度越高。然而,在子带级拉普拉斯分布噪声建模方法中,由于同一子带的残差系数对应相同的拉普拉斯参数,因此这种噪声建模方法赋予同一子带边信息相同的置信度,可能会导致DVC解码时,对高置信度边信息(具有小残差系数)赋予较低置信度,而对于低置信度边信息(具有大残差系数)赋予了较高置信度,这种参数估计的不合适会得到不准确的拉普拉斯分布噪声模型,使得拉普拉斯分布不能准确描述残差分布,从而降低了DVC的压缩效率。另一方面,由于拉普拉斯密度以指数率衰减,其尾部衰减与实际 DCT系数直方图统计中在重尾分布上有很大区别[7,8],所以它不能很好地描述大残差系数的分布特征。由以上分析可以看出,由于子带级的拉普拉斯参数估计法不准确以及拉普拉斯概率密度的尾部衰减方式与DCT重尾分布特性的不相符,因此,子带级的拉普拉斯分布模型不能很好地描述DVC中DCT残差的大系数和小系数的分布,或者说它不能精确地刻画出残差系数的重尾和尖峰分布特性。
图1给出了foreman序列的第88帧中的第1个AC (Alternating Current)子带的残差系数的直方图统计分布和相应拉普拉斯分布的比较,从图中可以看出,相应拉普拉斯分布模型跟真实的噪声分布相比,有很大的差异。相比拉普拉斯分布,DCT残差系数具有更陡峭的峰值特性和更长的尾部。
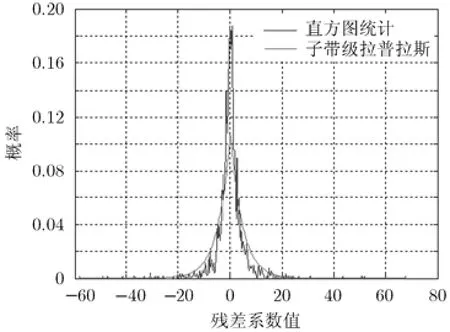
图1 foreman序列第88帧中的第1个AC子带残差系数直方图统计分布和相应的拉普拉斯分布比较
文献[7, 8]指出,柯西分布的尾部衰减很慢,具有重尾特性,更能逼近 DCT系数的尾部形态。根据柯西分布具有重尾特性这一特点,本文提出利用柯西分布来描述DVC中DCT残差系数分布的尾部特征,从而弥补拉普拉斯分布其尾部衰减方式的不足。针对子带级拉普拉斯分布由于其参数估计的不合适,使得高置信度边信息(具有小残差系数)被赋予较低置信度,导致拉普拉斯分布峰值不够尖锐这一缺点,本文提出了一种改进拉普拉斯参数估计法,从而提出一种新的残差系数分布模型,拉普拉斯-柯西混合分布(LDMD)模型。
3 LCMD相关噪声模型
由于在解码端利用原始的WZ帧信息来估计相关噪声模型可以达到性能的上界,因此,本节先介绍离线LCMD模型,然后再讨论在线LCMD噪声模型。
(1)离线LCMD噪声模型 在LCMD模型中,每个子带的DCT残差系数首先被分成小系数和大系数两类,大系数的分布用柯西分布来描述,小系数的分布用拉普拉斯分布描述,然后根据混合模型的特点计算出柯西分布和拉普拉斯分布的参数。该算法主要有如下4个实现步骤。
步骤1系数分类
在每个子带中,DCT残差系数被分成两个集合,小系数集S0和大系数集S1,其分类准则如下:
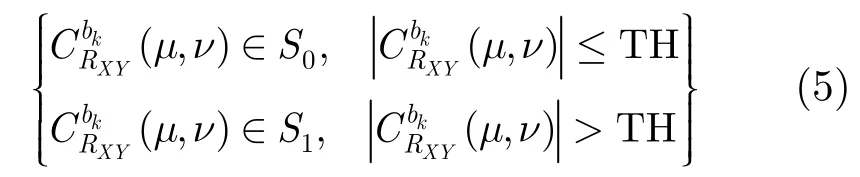
其中TH是分类阈值,它由式(6)获得:

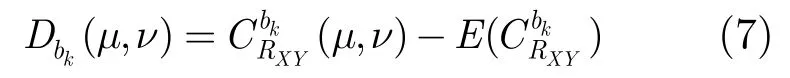
步骤2柯西分布参数估计
柯西分布可以表示为

其中λ和μ分别为形状和位置参数。考虑到视频压缩中残差系数基本关于0值对称,所以令μ=0。在本文中就只剩下参数λ需要估计。假设每个子带的系数分布可以由柯西概率密度或者拉普拉斯概率密度来描述,对于柯西分布,总可以找到一个λ,使得其概率密度在[-TH,TH]区间内的积分值等于拉普拉斯概率密度在[-TH,TH]区间内的积分值而依然可以保持它的重尾特性。以此思想为出发点,λ按如下过程估计:
令PL(TH)表示拉普拉斯概率密度在[-TH,TH]内的积分值,它可以按式(9)计算:

令PC(TH)表示柯西概率密度在[-TH,TH]内的积分值,按式(10)计算:

λ由式(11)计算:

步骤3LCMD中拉普拉斯分布参数的改进
按式(12)给属于S0集合的残差系数重新计算拉普拉斯参数:

步骤4LCMD噪声模型
本文所提的LCMD模型如式(13)所示:
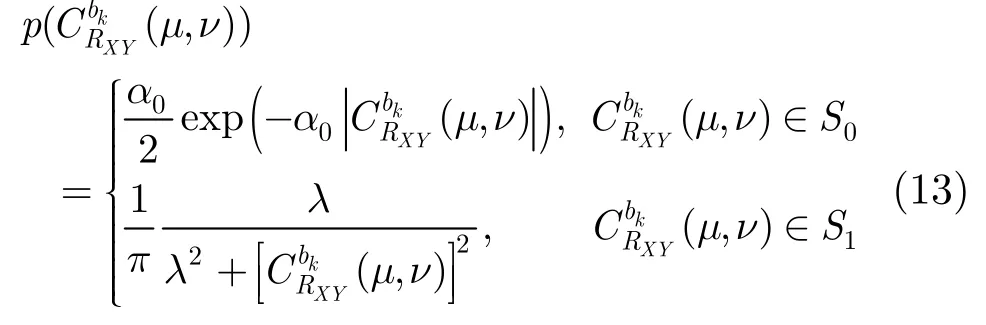
图2(a)为soccer序列的第88帧中的第1个AC子带的残差系数的直方图统计分布、子带级拉普拉斯分布、使用文中所提的柯西分布、以及本文改进后的拉普拉斯分布的比较,图中的阈值 TH=27 为使用文中分类方法求得。为更清楚的看出大系数的分布,图2(b)给出该子带中系数值大于阈值27时的几种分布的比较。从图2可以看出,相比子带级拉普拉斯分布,文中柯西分布更逼近真实 DCT残差系数的尾部分布形态(图中落在区间[-27, 27]外的系数为大残差系数,即对应重尾部分)。而调整后的拉普拉斯分布在[-27,27]之间具有很陡峭的峰值,非常接近真实残差系数的分布。
(2)在线LCMD噪声模型 由于在实际的DVC系统中,在解码端没有原始WZ帧数据,为了使所提相关噪声模型更实际,由式(4)所示的运动补偿残差帧RME被用来估计相关噪声模型,其他步骤则与离线情况下的LCMD模型相同。

图2 残差系数比较
4 实验结果及分析

图3给出了不同相关噪声模型下WZ帧的率失真(RD)曲线。由图3可见,无论是离线还是在线情况,本文所提LCMD噪声模型相比拉普拉斯噪声模型,DVC压缩性能都有所提高,而离线情况下的性能改善更加明显,文中提出的离线LCMD模型对3个序列的平均质量最大可以提高0.9 dB此外,与离线的拉普拉斯模型对比,在线的LCMD模型都能够获得较好的增益。
由实验还可以看出,3个序列中运动复杂度越高,其增益越大,原因是:运动越复杂的视频序列,其边信息的各个像素的质量差异越大,而LCMD模型中调整后的拉普拉斯分布由于更精确地描述了高精度边信息的置信度,所以高精度边信息置信度的描述跟真实的置信度的差异被大大缩小。此外,LCMD模型中的柯西分布较好地捕获了大残差系数分布的尾部信息,所以总体性能上运动复杂序列(如soccer序列)的增益就越大。由此也可以看出,运动越复杂,边信息质量越差,文中的LCMD模型对系统性能的提升越大。
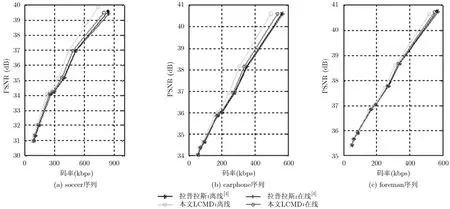
图3 本文LCMD模型对soccer, carphone和foreman序列的压缩性能
在计算复杂度上,分布式视频编码的解码计算量主要集中在边信息生成和Turbo码的迭代译码。由于利用所提出的 LCMD模型能更精确的计算出边信息与原始WZ帧的噪声模型,因此译码器只需较少的校验位和较少的迭代次数就可以纠正边信息错误而恢复出原始WZ帧,因此减少了计算量。与采用文献[4]的拉普拉斯模型相比,表1给出了不同序列在采用LCMD模型后译码时间的节省率。由实验结果可以看出,采用LCMD模型后,系统译码消耗时间对于不同运动复杂度的序列都有不同程度的减少。

表1 采用LCMD后系统译码时间的节省率(LCMD:所提模型,Lap:拉普拉斯模型)
5 结束语
本文提出了一种新的拉普拉斯-柯西混合分布噪声模型。在LCMD模型中,根据残差系数的绝对值将残差系数分成两类:小系数和大系数。小系数的分布由拉普拉斯分布来描述,大系数由柯西分布来描述。同时,提出两种确定分布参数的方法,一种是简单有效的柯西分布参数估计法,另一种是拉普拉斯参数改进方法。仿真结果表明,与典型的拉普拉斯模型相比,本文所提的离线和在线的LCMD模型均能产生较高的编码增益,尤其是对于较高运动强度的序列,其增益更明显。此外,采用LCMD模型可以降低TDWZ系统的解码复杂度。
[1]Slepian D and Wolf J. Noiseless coding of correlated information sources [J].IEEE Transactions on Information Theory, 1973, 19(4): 471-480.
[2]Wyner A and Ziv J. The rate-distortion function for source coding with side information at the decoder[J].IEEE Transactions on Information Theory, 1976, 22(1): 1-10.
[3]Brites C, Ascenso J, Pedro J Q,et al.. Evaluating a feedback channel based transform domain Wyner-Ziv video codec [J].Signal Processing:Image Communication, 2008, 23(2):269-297.
[4]Brites C and Pereira F. Correlation noise modeling for efficient pixel and transform domain Wyner-Ziv video coding[J].IEEE Transactions on Circuits and Systems for Video Technology, 2008, 18(9): 1177-1190.
[5]Huang X and Forchhammer S. Improved virtual channel noise model for transform domain Wyner-Ziv video coding[C]. IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), Taipei, China, 2009: 921-924.
[6]Martins R, Brites C, Ascenso J,et al.. Statistical motion learning for improved transform domain Wyner-Ziv video coding[J].IET Image Processing,2010, 4(1):28-41.
[7]Sergio S and Manuel D. Cauchy-density-based basic unit layer rate controller for H.264/AVC[J].IEEE Transactions on Circuits and Systems for Video Technology, 2010, 20(8):1139-1143.
[8]Chen L, Yang G B, and Ho A T. A Cauchy distribution based video watermark detection for H.264/AVC in DCT domain[C]. IEEE International Symposium on Circuits and Systems (ISCAS), Changsha, China, 2011: 2665-2668.
[9]Li Z, Liu L, and Delp E J. Rate distortion analysis of motion side estimation in Wyner-Ziv video coding [J].IEEE Transactions on Image Processing, 2007, 16(1): 98-113.
