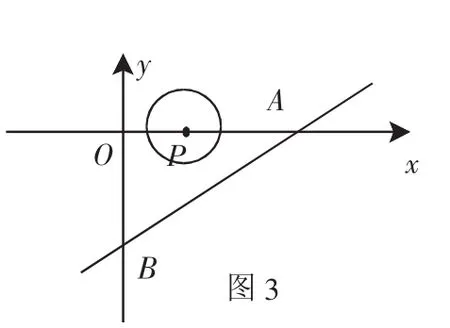
中考中有关动态圆问题解析

☉江苏省南京市江宁区铜井初级中学 朱宝庆

圆一直是中考考核的重点内容，近年来有关圆的动态变化已成为中考热门考点内容之一.在解题过程中只要抓住图形的变化规律与变化特点，灵活运用多种知识不难解决问题.下面分几种情况举例分析.

一、有关圆的滚动过程中特殊点的路线长

在中考中圆的滚动变化时，常会求某些特殊点的运动的路线长，其求解方法是能够描绘出该点运动过程的轨迹图形.

例1（2011年甘肃兰州市）已知一个半圆形工件，未搬动前如图1所示，直径平行于地面放置，搬动时为了保护圆弧部分不受损伤，先将半圆作如图1所示的无滑动翻转，使它的直径紧贴地面，再将它沿地面平移50m，半圆的直径为4m，则圆心O所经过的路线长是_______.（结果用π表示）

图1

分析：圆的运动包括三个部分，第一部分圆心平行移动；第二部分圆心围绕一点旋转；第三部分圆心沿地面再次进行平行移动，所以圆心O经过的路线长为三部分之和.

点评：此类问题关键要分析、掌握所求点的运动变化轨迹，并运用圆的相关知识进行求解.在本题中圆心两次围绕点进行旋转运动，根据它们各自特点进行求解.

二、有关圆的运动过程中图形的位置关系

有关圆的位置关系是中考考点中的重点内容，此类问题中要注意分类讨论思想的运用，考虑多种可能性的存在.

例2（2010年江苏泰州市）如图2在8×6的网格图（每个小正方形的边长均为1个单位长度）中，⊙A的半径为2个单位长度，⊙B的半径为1个单位长度，要使运动的⊙B与静止的⊙A内切，应将⊙B由图示位置向左平移_____个单位长度.

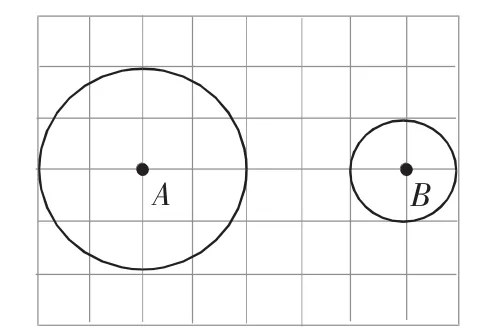
图2

分析：本题主要考查圆与圆的位置关系，在⊙B的运动过程中，有两次机会与⊙A相内切.当⊙B由图示位置向左平移4个单位时，第一次内切；6个单位时，第二次内切，所以本题答案为4或6.

点评：在圆与圆的位置关系中，相切是比较重要的概念，是考查的重点内容，它包括外切与内切.本题由于大圆半径为小圆半径的2倍，所以在运动过程中相内切时有两种可能，需要分类讨论.

分析：本题考查直线与圆的位置关系，在圆的运动过程中，圆的位置及大小都在变化，满足一定的变化规律.当圆与直线相切时，可以借助相似三角形的知识来求解线段的长度，最后根据线段长度和点运动的速度得到圆运动的时间.另外，在圆的运动过程中，圆有两次机会与直线相切，所以本题需要分类讨论进行求解.

但与工程管理专业的其他课程相比，该课程具有较强的专业知识综合性和复杂性，知识体系具有显著的系统性和抽象性。特别是对于一些砌体结构和钢筋混凝土结构中构件的构造设计，这些需要靠实际工程经验积累的，就需要学生具有一定的工程实践经验与体会，因此，这就给学生在工程结构课程中的学习带来了一定的难度。

图4

图5

点评：本题结合圆的运动、直线与圆的位置关系与相似知识求解.本题圆的运动变化不仅是圆的位置发生变化，圆的半径也同时变化，图形的变化比较灵活.

三、有关圆滚动的路程

求圆滚动的路程也是中考常会出现的题型，解决此类问题要综合分析圆在数学情境中的运动特点，结合几何图形性质综合求解.

例4（2010年山东威海市）如图6，在▱ABCD中，∠DAB=60°，AB=15cm.已知⊙O的半径等于3cm，AB，AD分别与⊙O相切于点E，F.⊙O在▱ABCD内沿AB方向滚动，与BC边相切时运动停止.试求⊙O滚过的路程.

分析：求圆滚动过的路程，只要求出两圆心间的距离即可.由于圆与平行四边形两边相切，所以过圆心作平行四边形的一边的垂线即可得出⊙O滚过的路程的线段.

因为AB，AD分别与⊙O相切于点E，F，

所以OE⊥AB，OE=3.

由∠DAB=60°可得∠OAE=30°.

图7

因为AD∥BC，∠DAB=60°，所以 ∠ABC=120°.

设当运动停止时，⊙O与BC，AB分别相切于点M，N，连接ON，OB.

点评：把求圆的滚动路程问题转化为求线段的长度，综合运用平行四边形、直线与圆相切、三角函数等相关知识求解，体现中考命题的综合性特点.

综上所述，解决与圆有关的滚动变化问题的关键要明确圆运动变化的特点，巧妙结合图形性质特点综合进行求解.