例说一道习题在中考试题中的演变

☉湖北省襄阳诸葛亮中学 韩春见

课本中重要的例题和习题、数学活动材料等反映数学理论的本质属性，通过类比、延伸、迁移、拓广，提出新的问题加以解决，能有效地巩固基础知识、发展数学能力.事实上，许多中考试题都源于课本，因此，注重课本中例习题的练习与变式，不仅能训练学生的理解和表达的能力，而且能训练学生审题和触类旁通的能力.本文以人教版八年级上册《轴对称》第58页第11题为例加以说明.

原题回顾：如图1，△ABD、△AEC都是等边三角形，求证：BE=DC.

分析：要证BE=DC，只需给线段BE和DC寻找到三角形，证明其所在三角形全等即可.从图1看，含有线段BE的三角形有△ABE和△CBE，含有线段DC的三角形有△ADC和△BDC.分辨后知需证△BAE≌△DAC.由等边三角形的性质可知这两个三角形有两边分别对应相等（即AB=AD，AE=AC），因此，只要证出两边的夹角（即∠BAE=∠DAC）相等.

证明：因△ABD、△AEC都是等边三角形，

所以AB=AD，所以AE=AC，∠BAD=∠EAC=60°.

所以∠BAD+∠BAC=∠BAC+∠EAC，即∠BAE=∠DAC.

在△BAE与△DAC中，

评注：本题以△ABC的AB、AC为边作等边△ABD和等边△AEC，构成了有共同顶点的两个等边三角形的基本图形.由于其具有典型性，所以在《轴对称》习题中，占有十分重要的地位.之所以这样说，是因为在全国各地中考中，以此题为背景，进行变式而新生的题目，十分普遍，考查方式类形也十分灵活，体现了课本原型题是中考命题的源泉.下面以2011年中考相关试题加以说明.

变式1：变换图形

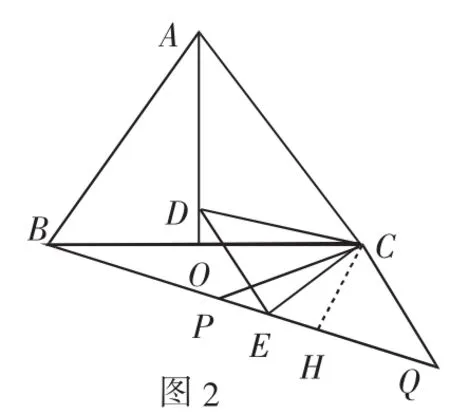
例1（2011年重庆綦江区）如图2，等边△ABC中，AO是∠BAC的角平分线，D为AO上一点，以CD为一边且在CD下方作等边△CDE，连接BE.

（1）求证：AD=BE.

（2）延长BE至Q，P为BQ上一点，连接CP、CQ使CP=CQ=5，若BC=8时，求PQ的长.

分析：要证AD=BE，就是证明△ACD≌△BCE.（2）由条件等边△ABC中，AO是∠BAC的角平分线，由三线合一，可知∠CBH=∠CAO=30°.PQ的长是等腰△CPQ的底边长，故可考虑过点C作CH⊥BQ，利用30°角所对的直线边等于斜边的一半，求得CH=4.在Rt△CHQ中，利用勾股定理可得HQ=3，从而可得PQ=2HQ=6.

（1）证明：因为△ABC和△CDE均为等边三角形，

所以AC=BC，CD=CE.且∠ACB=∠DCE=60°，

所以∠ACB-∠DCB=∠DCE-∠DCB，∠ACD=∠BCE.

所以△ACD≌△BCE（SAS），所以AD=BE.

（2）解：作CH⊥BQ交BQ于点H.

因为CP=CQ=5，所以PQ=2HQ.

因为△ABC为等边三角形，所以∠BAC=60°.

图3

评注：本题和课本原习题的构图方式一样，即以△BCD的边BC和CD分别为等边△ABC和等边△CDE的边，得出了比原习题更复杂更深刻的结论，其实质是课本例习题的拓广与延伸.通过本题说明，这种课本例习题的变式，是图形的位置发生了改变，但相关的线段仍具有相同的数量关系和位置关系.解决以有共顶点的两个等边三角形为基本构图的问题，寻找到题目中的全等三角形，进而寻找到对应角和对应线段是解答问题关键.

变式2：改变条件

例2（2011年浙江义乌市）如图3，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，四边形ACDE是平行四边形，连接CE交AD于点F，连接BD交CE于点G，连接BE.下列结论中：

①CE＝BD；②△ADC是等腰直角三角形；

③∠ADB＝∠AEB；④CD·AE＝EF·CG.

其中一定正确的结论有（ ）.

A.1个 B.2个 C.3个 D.4个

分析：（1）证明CE＝BD，就是证明线段CE和BD所在的三角形全等，即△ACE≌△ABD；（2）证明△ADC是等腰直角三角形，可借助四边形ACDE是平行四边形，证明△ADC≌△DAE；（3）证明∠ADB＝∠AEB，可证明∠ADB和∠AEB所在的三角形全等，即△ABD≌△ABE；（4）证明CD·AE＝EF·CG，就是证明这四条线段所在的三角形相似，利用三点定（三角形）型法，只需证明△CDG∽△EFA即可得到结论.

解：（1）因为△ABC和△ADE是等腰直角三角形，∠BAC＝∠DAE＝90°，

所以AB＝AC，所以AD＝AE，∠BAC＋∠CAD＝∠CAD＋∠DAE，即∠BAD＝∠CAE.

所以△BAD≌△CAE（SAS），所以CE＝BD.

（2）因△ADE是等腰直角三角形，所以∠ADE＝∠AED＝45°.

因四边形ACDE是平行四边形，所以∠ACD＝∠AED＝45°，AC∥DE，CD∥AE0.

所以∠ADC＝∠DAE＝90°，∠CAD＝∠ADE＝45°，所以△ADC是等腰直角三角形.

（3）由（2）知∠CAD＝∠ADE＝45°，

所以∠BAD＝∠BAC＋∠CAD＝90°＋45°＝135°.

∠BAE＝360°－∠BAC－∠CAD－∠DAE

＝360°－90°－45°－90°＝135°.

所以∠BAD＝∠BAE＝135°.

又AB＝AB，AD＝AE，所以△BAD≌△BAE（SAS），所以∠ADB＝∠AEB.

（4）由（1）知△BAD≌△CAE，所以∠ADB＝∠AEC，

所以∠CGD＝∠ADB＋∠GFA

＝∠AEC＋∠AFE＝180°－∠DAE＝180°－90°＝90°，

所以∠CGD＝∠FAE＝90°.

由（2）知，CD∥AE，所以∠DCG＝∠AEF，

所以△CDG∽△EFA，

评注：和原习题相比较，我们可以清楚的看到，本题是将原习题的等边三角形改为等腰直角三角形，合理而巧妙地变换了原题的条件.另外，本题作为结论开放题，一方面说明原习题改变后其考查方式和结论较多，较好地体现了课本是变式的基础，另一方面要注重结论开放题的解法 （即采用 “执果索因”的方法），需要学生根据所掌握的知识进行逆向思维逐步解答.这种题不仅可以考查不同层次学生的能力水平，而且对分层教学起着导向作用.

变式3：互换因果

例3 （2011年湖北荆州市）如图4，P是矩形ABCD下方一点，将△PCD绕P点顺时针旋转60°后恰好D点与A点重合，得到△PEA，连接EB.

（1）问△ABE是什么特殊三角形.请说明理由.

（2）连接DE、PB，求证：DE＝PB.

图4

分析：（1） 从△ABE的形状看，应猜想为等边三角形.由△PEA是将△PCD绕P点顺时针旋转60°后得到的可知，△APD为等边三角形.结合矩形ABCD，得到BE＝DC＝AB，∠EAP＝∠PAB＝∠CDP＝30°，可知∠EAB＝60°，从而证明△ABE为等边三角形.（2）证明DE＝PB，就是证明△ADE≌△APB.

（1）解：△ABE是等边三角形.理由如下.

因为△PEA是将△PCD绕P点顺时针旋转60°后得到的，

所以△PEA≌△PCD，且∠DPA＝60°，因为AE＝DC，PD＝PA，∠EAP＝∠CDP，

所以△ADP为等边三角形，所以∠PDA＝∠PAD＝60°.

又因为四边形ABCD是矩形，所以∠CDA＝∠BAD＝90°，DC＝AB，

所以AE＝AB，∠EAP＝∠CDP＝90°－∠PDA＝30°，

∠PAB＝90°－∠PAD＝30°，

所以∠EAB＝∠EAP＋∠PAB＝60°，△ABE是等边三角形.

（2）证明：由（1）知△ADP和△ABE均为等边三角形，

所以∠DAP＝∠EAB＝60°，AD＝AP，AE＝AB.

所以∠DAP－∠EAP＝∠EAB－∠EAP，所以∠DAE＝∠PAB.所以△ADE≌△APB（SAS），DE＝PB.

评注：本题是以有共顶点的两个等边三角形为基本构图，和基本习题不同的地方在于，原习题的条件是有共顶点的两个等边三角形，而本题是条件已知一个等边三角形，结论要求证一个等边三角形，即把原习题中的一个条件交换到结论中去，属原习题的变式问题.解题的关键在于观察试题与原习题的相同点与不同点、找准其内在规律，调整推理的顺序.

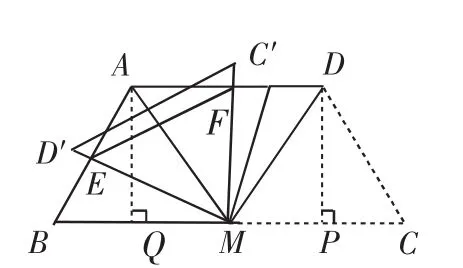
图5

变式4：增加条件

例4（2011年四川南充市）如图5，等腰梯形ABCD中，AD∥BC，AD＝AB＝CD＝2，∠C＝60°，M是BC的中点.

（1）求证：△MDC是等边三角形.

（2）将△MDC绕点M旋转，当MD（即MD′）与AB交于一点E，MC即MC′）同时与AD交于一点F时，点E，F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值.

分析：（1）要证△MDC是等边三角形，只需证明其有两条边相等.（2）本小题的关键在于如何转化.利用△BME≌△AMF，知△MEF为等边三角形，从而△AEF周长的最小值只需EF最小的问题，转化为求ME（或MF）最短的问题，利用垂线线最短，可求得MF的最小值为点M到AD的距离，故△AEF的周长的最小值为2+.

（1）略证：过点D作DP⊥BC于点P，过点A作AQ⊥BC于点Q.

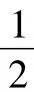
又因ADPQ是矩形，AD=PQ，所以BC=2AD.

由已知，点M是BC的中点，所以BM=CM=AD=AB=CD，

即△MDC中，CM=CD，∠C=60°，故△MDC是等边三角形.

（2）略解：△AEF的周长存在最小值，理由如下.

连接AM，由（1）平行四边形ABMD是菱形，△MAB，△MAD和△MC′D′是等边三角形.

∠BMA=∠BME+∠AME=60°，∠EMF=∠AMF+∠AME=60°，所以∠BME=∠AMF.

在△BME与△AMF中，BM=AM，∠EBM=∠FAM=60°，

所以△BME≌△AMF（ASA），所以BE=AF，ME=MF，AE+AF=AE+BE=AB.

因为∠EMF=∠DMC=60°，所以△EMF是等边三角形，EF=MF.

MF的最小值为点M到AD的距离.

△AEF的周长=AE+AF+EF=AB+EF，所以△AEF的周长的最小值为2+.

评注：本题进一步将原习题深化.试题中，以M为等边三角形一个点，共出现5个等边三角形.找到合适共顶点M的等边三角形，并寻找到全等三角形（△BME≌△AMF）是解决问题的关键.这就要求学生在平时学习时要围绕某些典型问题进行集中训练，以培养以点带面，触类旁通的能力.

变式5：改变图形的呈现方式

例5（2011年湖北孝感市）如图6，等边△ABC内接于⊙O，P是弧AB上任一点（点P不与点A、B重合）.连AP、BP，过点C作CM∥BP交PA的延长线于点M.

（1） 填空：∠APC=______度，∠BPC=______度.

（2）求证：△ACM∽△BCP.

（3）若PA=1，PB=2，求梯形PBCM的面积.

图6

分析：（1）利用同弧所对圆周角相等和等边△ABC，可得∠APC和∠BPC度数均为60°.（2）利用CM∥BP，知∠M=60°，故∠M=∠BPC.利用同角的补角相等，知∠MAC=∠PBC，可证△ACM∽△BCP.（3）证△PCM为等边三角形，可求出梯形的上下底长分别为1和3，过点P作PH⊥CM，可得PH长，从而求出梯形PBCM的面积.

（1）60，60.

（2）证明：因CM∥BP，所以∠BPM+∠M=180°，∠PCM=∠BPC=60°.

所以∠M=180°-∠BPM=180°-（∠APC+∠BPC）=60°，解得∠M=∠BPC=60°.

因四边形APBC内接⊙O，所以∠PBC+∠PAC=180°.

又∠PAC+∠MAC=180°，所以∠MAC=∠PBC，所以△ACM∽△BCP.

（3）解：由（1）（2）知∠APC=∠PCM=∠M=60°，△ACM∽△BCP，

所以△PCM为等边三角形，∠BCP=∠ACM，所以CP=CM=PM.

因△ABC为等边三角形，所以BC=AC，所以△ACM≌△BCP（SAS），所以AM=BP=2，

所以CP=CM=PM=AP+AM=1+2=3.

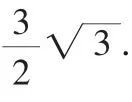
评注：本题将等边△ABC与等边△PCM用圆作为背景呈现出来，加大了寻找基本构图（有公共顶点的两个等边三角形）的难度.因此，从图形中找到△ACM≌△BCP，是解决问题的关键.通过本题说明，解答改变了课本例习题的文字叙述或图形的呈现方式的试题，从复杂的试题背景中找到基本图形或基本例习题，对于解决问题很重要，它能为解题提供思路.

变式6：加大问题的深度和广度

例6（2011年浙江义乌市）如图7，在等边△ABC中，点D是边AC的中点，点P是线段DC上的动点（点P与点C不重合），连接BP.将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P，连接AA1，射线AA1分别交射线PB、射线B1B于点E、F.

图7

图8

（1）如图7，当0°＜α＜60°时，在α角变化过程中，△BEF与△AEP始终存在关系______（填“相似”或“全等”），并说明理由.

（2）如图8，设∠ABP=β.当60°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由.

（3）如图9，当α=60°时，点E、F与点B重合.已知AB=4，设DP=x，△A1BB1的面积为S，求S关于x的函数关系.

分 析：（1） 要 证 △BEF∽△AEP，只需证明这两个三角形有两对对应角相等即可.（2）由（1）△BEF与△AEP相似，若全等，只需对应边BE=AE，可得∠BAE=∠ABE.从而找到α=2β+60°.（3）由于△APB≌△A1PB1知A1B1=AB=4，且A1B1∥AC，故连接BD交A1B1于点G，则BG为△A1BB1的高.

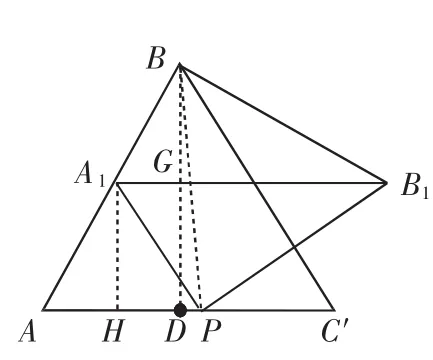
图9

解：（1）相似.理由如下.

由题意得：∠APA1=∠BPB1=α，AP=A1P，BP=B1P，

因∠PBB1=∠EBF，所以∠PAE=∠EBF.又因∠BEF=∠AEP，所以△BEF∽△AEP.

（2）存在，理由如下易得：△BEF∽△AEP.

若要使得△BEF≌△AEP，只需要满足BE=AE即可，所以∠BAE=∠ABE.

（3）连接BD，交A1B1于点G，过点A1作A1H⊥AC于点H.

因∠B1A1P=∠A1PA=60°，所以A1B1∥AC.

在Rt△ABD中，BD=2，所以BG=BD-DG=BD-A1H=

评注：本题第（3）小问有两组有共公顶点的等边三角形，一组是等边△BAC和等边△BPB1，另一组是等边△PAA1和等边△PBB1作为试题背景，将判断说理、结论开放与函数问题有机地结合起来，覆盖面广，运用知识和方法之多是一般综合题无法比拟的.这种题主要考查学生基本概念、图形的清晰程度和分析问题的全面性等.在平时的学习中，学生除了应学会解题外，还要利用重要习题编题并能提出问题，它比纯粹解决问题更能训练思维的缜密性和严谨性，也更有利于学生在水平测试中迅速看出试题在课本中的影子，并找到问题解决的突破口.