蹊跷的压轴题答案

☉陕西省洋县黄安初中 邓文忠

原题（2012年陕西压轴题）如图1，正三角形ABC的边长为3+.

（1）如图1，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上.在正三角形ABC及其内部，以A为位似中心，作正方形EFPN的位似正方形E′F′P′N′，且使正方形E′F′P′N′的面积最大（不要求写作法）；

（2）求（1）中作出的正方形E′F′P′N′的边长；

（3）如图2，在正三角形ABC中放入正方形DEMN和正方形EFPH，使得DE、EF在边AB上，点P、N分别在边CB、CA上，求这两个正方形面积和的最大值及最小值，并说明理由.

标准答案（1）如图1，正方形E′F′P′N′即为所求.

（2）设正方形E′F′P′N′的边长为x.

因△ABC为正三角形，

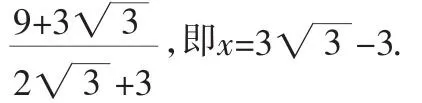
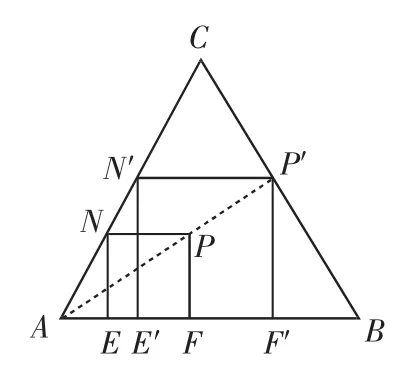
图1

（3）如图2，连接NE，EP，PN，则∠NEP=90°.

设正方形DEMN、正方形EFPH的边长分别为m、n（m≥n），它们的面积和为S，则NE=m，PE=n.

所以PN2=NE2+PE2=2m2+2n2=2（m2+n2）.

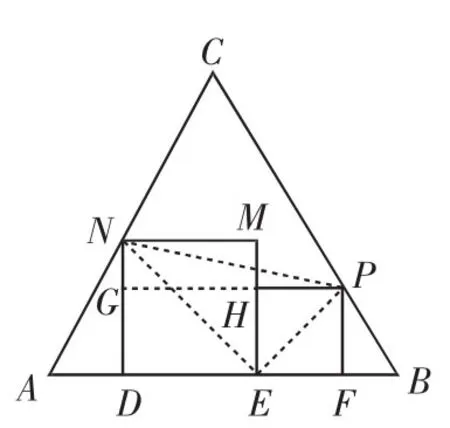
图2

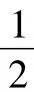
延长PH交ND于点G，则PG⊥ND.

在Rt△PGN中，PN2=PG2+GN2=（m+n）2+（m-n）2.

所以①当（m-n）2=0时，即m=n时，S最小.

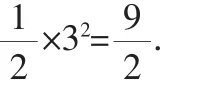
②当（m-n）2最大时，S最大.即当m最大且n最小时，S最大.

笔者为此进行了专门的研究，特别是注意到S=m2+n2和m+n=3两式，灵机一动，此题可消元转化为二次函数模型.

简解：设正方形DEMN、正方形EFPH的边长分别为m、n（m≥n），它们的面积和为S.

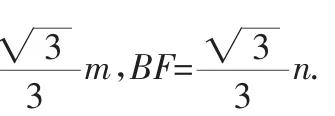
因AB=3+，所以.所以m+n=3.

因m≥n，由（2）知，m最大=3-3，所以≤m≤3-3.

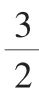
当m=3-3时，S最大=

一个细节：在上面设法中注明了m≥n，原题上没有，若去掉这个条件又怎样求m的取值范围？

因m+n=3，

所以n=3-m.

又0＜m≤3-3， ①

所以由对称性知0＜n≤3-3，即0＜3-m≤3-3. ②

只需求S=m2+n2=m2+（3-m）2=2m2-6m+9（6-3≤m≤3-3）的最值了.

此时当m=6-3或3-3时，S最大=99-54

到此，孰优孰劣，一看便知.

由此可见，解决数学问题应尽量分清主次，捕捉和把握题目本质，突出通性通法，揭示规律，同时，选择一个合适的方向确实能起到四两拨千斤之效，以最简捷、明了的方法达到解决问题之目的，使人一目了然、心旷神怡，令人豁然开朗.追求简易，享受数学简洁之美，让我们记住单墫先生的话吧“：解法应以简单，自然为止，避免‘废招’”.