新课标下初中数学要强化思想方法的教学

☉江苏省盐城市明达中学 刘国成

数学中考题要体现义务教育性质，要面向全体学生，关注每一个学生的发展.试题的设计充分重视原创，体现能力立意，不考死记硬背.在解题方法上重视对数学通性通法的考查，努力体现新课程的理念，在学生已有知识经验和与知识体系相关的现实背景中，考查基础知识和基本技能、数学活动过程、数学思考、解决问题能力，突出考查了学生运用数学知识解决实际问题的能力，加大对学生后继学习潜能的考查，对学生的情感、态度、价值观的形成起到了积极的影响，让学生切实感受到了现实生活中有大量的数学信息.本文以2012年几道关于等腰三角形边的中考数学试题为例说明.

例1（1）（黑龙江省绥化市）若等腰三角形两边长分别为3和5，则它的周长是_______.

解析：已知条件中并没有指明3和5谁是腰长，因此应由三角形的三边关系进行分类讨论.当3是腰长时，这个等腰三角形的底边长就是5，此时的等腰三角形的周长等于11；当5是腰长时，这个三角形的底边长就是3，此时周长等于13.故这个等腰三角形的周长等于11或13.

（2）（江苏省常州市）已知三角形两条边长分别为4，9，则这个等腰三角形的周长为_________.

A.13 B.17 C.22 D.17或22

解析：已知条件中并没有指明4和9谁是腰长，因此应由三角形的三边关系进行分类讨论.当4是腰长时，这个等腰三角形的底边长就是9，此时的等腰三角形不存在；当9是腰长时，这个三角形的底边长就是4，此时周长等于22.故这个等腰三角形的周长等于22.

（3）（贵州省遵义市）一个等腰三角形的两条边长分别为4cm和8cm，则这个三角形的周长为______cm.

解析：已知条件中并没有指明4和8谁是腰长，因此应由三角形的三边关系进行分类讨论.当4是腰长时，这个等腰三角形的底边长就是8，此时的等腰三角形不存在；当8是腰长时，这个三角形的底边长就是4，此时周长等于20.故这个等腰三角形的周长等于20.

例2（湖北省随州市）等腰三角形的周长为16，其一边长为6，则另两边为______.

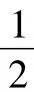
例3（辽宁省沈阳市）如图1，正方形ABCD中，对角线AC，BD相交于点O，则图中的等腰直角三角形有（ ）.

A.4个 B.6个

C.8个 D.10个

图1

解析：已知条件中并没有指明等腰直角三角形哪是底哪是腰，因此要分类讨论.当AD、DC、AB、BC为腰时，等腰直角三角形有 △ACD、△ABD、△BCD、△ABC共4个；当AD、DC、AB、BC为底时，等腰直角三角形有△ABO、△ADO、△BCO、△CDO共4个.所以图中的等腰直角三角形有8个.答案选C.

例4（江苏省苏州市）在3×3的方格纸中，点A、B、C、D、E、F分别位于如图2所示的小正方形的顶点上.从A、D、E、F四个点中任意取一点，以所取的这一点及点B、C为顶点画三角形，则所画三角形是等腰三角形的概率为______.

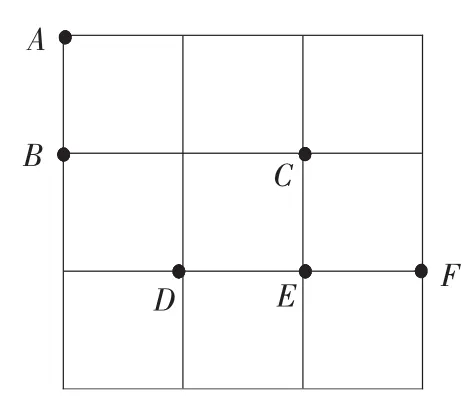
图2

解析：根据从A、D、E、F四个点中任意取一点，一共有4种可能：△ABC、△DBC、△BCE、△BCF.只有选取D点时，所画三角形△DBC是等腰三角形，取A、E、F点所画三角形△ABC、△BCE、△BCF不是等腰三角形.故所画三角形是等腰三角形的概率为0.25.

例5（辽宁省丹东市）如图3，边长为6的正方形ABCD内部有一点P，BP=4，∠PBC=60°，点Q为正方形边上一动点，且△PBQ是等腰三角形，则符合条件的Q点有_____个.

图3

解析：本题的实质是已知等腰△PBQ的一边为BP，要我们在正方形边上找一动点Q，使△PBQ为等腰三角形，题目的条件中并没有指明BP是腰还是底，因此要分别就BP是腰、底两种情况进行讨论.当BP是底时，这个等腰三角形的顶点Q就是BP的垂直平分线与正方形ABCD的交点，有2个；当BP是腰时，Q就是分别以B、P为圆心、BP为半径画弧与正方形ABCD的交点，共5个（重合的算1个）.

对于有关等腰三角形边的问题，当底和腰不等时，若条件中没有明确哪是底哪是腰时，应在符合三角形三边关系的前提下分类讨论，这类内容虽然不难，但是失分率较高.因此我们在今后的初中数学教学过程中要根据2011版初中数学课程标准的要求将“数学学习”和“数学教学”两条合并成一条“教学活动”，

通过操作、观察、归纳等数学活动获得数学结论并准确地表达自己的思考过程，进行重点强化教学，不仅注重对学生基本知识、基本技能的教学，而且特别要注重数学的基本思想与方法、思考过程与思考能力的教学，促进学生的全面发展.

1.沈文选.中学数学思想方法.长沙：湖南师范大学出版社，1999.

2.郑金洲.教师如何做研究.上海：华东师范大学出版社，2005.

3.2012年各省市中考数学真题汇编，中考资源网.

4.义务教育数学课程标准（2011版）.北京：北京师范大学出版社，2012.