平淡中见素质 细节中见功底——对解一元一次方程一节课的反思

☉江苏省扬州大学附属中学东部分校 许 苗

我们每天的教育实践虽然平凡、繁琐，但是只要我们在实践中反思，在反思中实践，那么每一件小事都会富有价值和意义，这是教育家区别于教书匠的根本所在.我们只要勤于反思、善于反思，才能使自己的思维始终处于年轻活跃的状态，才能不断产生新的思想，才能点燃学生心中那求知的欲望.反之，一个不会思考或者懒于思考的教师，他只能机械地搬运现成的、僵化的知识来讲授，来说教，而这在充满好奇、渴望探索的学生面前，自然显得那样乏味，没有任何学习的魅力.学生会滋生出失望、不满、懈怠，甚至也会像老师那样懒于思考.失去了思考，就失去了学习的兴趣和探索的乐趣，也就没有的灵魂，没有了个性.书本上的知识只有在思考者的手中才能化成真正的智慧，教师的思考使书本上的知识增加了“附加值”，增加了“情感动力”.

下面是对解一元一次方程这样一节普普通通数学课的反思，求教于一线老师，若我的反思能给你带来一点收益，那正是笔者行文价值之所在！

一、移项——朝哪个方向移？是左移还是右移？一定右移吗

解法一：去分母，得4（x+14）=7（x+20）；

去括号，得4x+56=7x+140；

移项、合并同类项，得-3x=84；

方程两边同除以-3，得x=-28.

解法二：去分母，得4（x+14）=7（x+20）；

去括号，得4x+56=7x+140；

移项、合并同类项，得-84=3x；

方程两边同除以3，得-28=x；

即：x=－28.

反思：法一是教材讲的方法，在移项时一般是把含有未知数的项移到等号的左边，把常数项移到等号的右边.这样做的好处是：除去系数后即得习惯答案，但它的缺点是除去系数时容易出错.法二是笔者的方法，在移项时一般是把含有未知数的项移后使系数为正，这样做的好处是：未知数的系数为正除去后不易出错；但它的缺点是除去系数后时常需要转化习惯答案，这样往往多一步运算.比较这两种做法，我们既体会到法一因习惯做法固化后带来的通性通法的力量，又体会到法二不拘常规的解法带来思维的灵性.

二、移项后变号变得是什么符号——是运算符号还是数的符号

例2解方程：5x－2=8（鲁教版六年级上册课本109页）.

解法一：移项，得5x=8+2；

合并同类项，得5x=10；

方程两边同除以5，得x=2.

解法二：移项得：5x=8－（－2）；

合并同类项，得5x=10；

方程两边同除以5，得x=2.

解法三：由原题得，5x+（－2）=8；移项，得5x=8-（-2）；

合并同类项，得5x=10；

方程两边同除以5，得x=2.

反思：根据移项的定义，把原方程中的项改变符号后，从方程的一边移到另一边，改变的是运算符号还是数的符号？从解法一的过程来看，改变的是运算符号！但解法二、三改变的是数的符号！解法一更简洁明了，解法二、三更另类新奇.

三、一元一次方程的解法有几种？——两种？还是三种

例3解方程：5x－2=8.

解法一：由减法的逆运算，得5x=8+2；

合并同类项，得5x=10；

方程两边同除以5，得x=2.

解法二：把原方程两边都加上2，得5x－2+2=8+2；

即5x=8+2；

合并同类项，得5x=10；

方程两边同除以5，得x=2.

解法三：移项得，5x=8+2；

合并同类项，得5x=10；

方程两边同除以5，得x=2.

反思：法一用的是加减法的逆运算，方法原始而古老；法二用的是等式的性质，啰嗦而固执；法三是总结了前两种解法的精华，简洁而灵巧.

四、移项法解一元一次方程的步骤是几步？——四步？还是五步

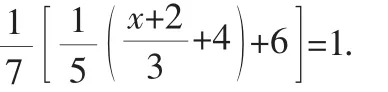
两边同乘以3，得x=1.

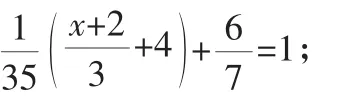
两边同乘以35×3，得x=1.

反思：移项法解一元一次方程的步骤常见的有五步：去分母、去括号、移项、合并同类项、系数化为1.法一就是按照这五个步骤来求解的.当然每一个题目求解的步骤不一定是五步，有的步骤可以省略，顺序可以改变.很明显法二缺少去分母一步，因为它与系数化为1这一步有点重复.智者见智，仁者见仁，移项法解一元一次方程的步骤不管采用四步法还是五步法，都要牢固掌握该步骤下的相关知识，顺利准确地求解.

我们的教学工作虽然平淡，但在平淡的工作中更见一个人的素质——天下难事，必成于易；我们的课堂教学虽然平凡，但在平凡的细节中更见一个人的功底——天下大事，必做于细；我们的工作范围狭小，但你的心有多宽，梦就有多远，根就有多深，你的天地就有多大，你的事业就有多辉煌，你的生命就有多精彩！

如果你这么想，更重要的是你长期这样做了——甘于平淡，认真做好每一个细节，或许我们听不到你生命中拔节的声音，但我们可以预言，一个有思想的教师——一个教育名家——一代宗师即将诞生！