例析用不等式组模型解决现实生活中的方案设计问题

2012-07-25江苏省江阴市利港中学

中学数学杂志 2012年20期

☉江苏省江阴市利港中学刘杰

不等式组与方程组一样，是解决现实生活中的重要模型，主要涉及经济类、劳力分配、方案设计等方面的问题，是中考的热点题型，下面精选几例加以分析.

一、服装生产方案问题

例1下岗职工王阿姨利用自己的一技之长开办了“爱心服装厂”，计划生产甲、乙两种型号的服装共40套投放到市场销售.已知甲型服装每套成本34元，售价39元；乙型服装每套成本42元，售价50元.服装厂预计两种服装的成本不低于1536元，不高于1552元.问服装厂有哪几种生产方案.

分析：首先阅读题意，抓住关键词：“不低于”、“不高于”来建立不等式，组成不等式组，然后解不等式组.

解：设甲型服装x套，则乙型服装为（40-x）套，由题意得1536≤34x+42（40-x）≤1552.

解得16≤x≤18.

因x是正整数，

所以x=16或17或18.有以下三种生产方案：

生产甲型服装16套，乙型24套或甲型服装17套，乙型23套或甲型服装18套，乙型服装22套.

点评：用不等式组解决应用问题，关键是分析题意，寻找不等关系，列出不等式组.要善于将题目中的数量关系转化为不等式组，并且解不等式组所得的结果通常为一解集，需要从解集中再找出符合题意的答案.

二、商店进货方案问题

例2某商店需要购进一批电视机和洗衣机，根据市场调查，决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表：

类别洗衣机进价（元/台） 1800 1500电视机

计划购进电视机和洗衣机共100台，商店最多可筹集资金161800元.

请你帮助商店算一算有多少种进货方案.（不考虑除进价之外的其他费用）

分析：本题中提供了电视机和洗衣机的进价，由于不考虑进价之外的其他费用，因此，设购买其中一个物品的台数为x，那么根据题意，列出两个一元一次不等式，组成不等式组.由于要求的是进货方案，因此x的值应取正整数.

解：（1）设商店购进电视机x台，则购进洗衣机（100-x）台，根据题意，得

即购进电视机最少34台，最多39台，商店有6种进货方案.

点评：本题是以表格的形式展示数字信息，根据题目中的关键词“不少于”和“最多”来建立不等式，组成不等式组，然后加以解决.

三、租车方案问题

例3某校准备组织290名学生进行野外考察活动，行李共有100件.学校计划租用甲、乙两种型号的汽车共8辆，经了解，甲种汽车每辆最多能载40人和10件行李，乙种汽车每辆最多能载30人和20件行李.

（1）设租用甲种汽车x辆，请你帮助学校设计所有可能的租车方案.

（2）如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元，请你选择最省钱的一种租车方案.

分析：（1）通过阅读题目，不难发现题目中存在这样的不等关系“：载客量总和应该达到或超过290名”“、载行李量总和应该达到或超过100件”.根据这两个不等关系建立不等式组，从而可求出x的取值范围，最后再确定所有可能的租车方案；（2）计算（1）中的每一种租车方案所需要的费用，然后进行比较，从中选择出最省钱的租车方案.

解：（1）由于租用甲种汽车x辆，则租用乙种汽车（8－x）辆.由题意得

因为x取整数，所以x=5，6.

所以共有两种租车方案：第一种是租用甲种汽车5辆，乙种汽车3辆；第二种是租用甲种汽车6辆，乙种汽车2辆.

（2）第一种租车方案的费用为5×2000＋3×1800=15400（元）；第二种租车方案的费用为6×2000＋2×1800=15600（元）.所以，第一种租车方案更省费用.

点评：本题文字较多，关系较复杂，解决本题需要仔细读题，理解题意，从而挖掘出题目中所隐含的不等关系，从而建立不等式组模型来进行求解.

四、工厂生产方案

例4（2012年湖南常德）某工厂生产A、B两种产品共50件，其生产成本与利润如下表：

利润（万元/件）A种产品0.6 B种产品0.9利润（万元/件） 0.2 0.4

若该厂计划投入资金不超过40万元，且希望获利超过16万元，问：工厂有哪几种生产方案？哪种生产方案获利最大？最大利润是多少？

分析：根据“投入资金不超过40万元，获利超过16万元”可列出不等式组，求得不等式组的整数解即可确定生产方案，再通过计算，确定获利最大的生产方案.

解：（1）设生产A种产品x件，则生产B种产品（50－x）件，根据题意，得

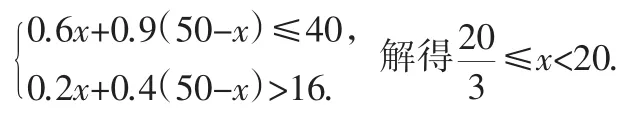
因为x取正整数，所以x＝17，18，19.

所以有三种生产方案：

方案一：生产A种产品17件，生产B种产品33件；

方案二：生产A种产品18件，生产B种产品32件；

方案三：生产A种产品19件，生产B种产品31件.

（2）（法一）因为B种产品每件获得的利润多，所以应多生产B种产品.

即生产A种产品17件，生产B种产品33件，获利最大，最大利润是17×0.2＋33×0.4＝16.6（万元）.

（法二）方案一：获利是17×0.2＋33×0.4＝16.6（万元）；

方案二：获利是18×0.2＋32×0.4＝16.4（万元）；

方案三：获利是19×0.2＋31×0.4＝16.2（万元）.

因为16.6＞16.4＞16.2，所以方案一获利最大.

即生产A种产品17件，生产B种产品33件，获利最大，最大利润是16.6万元.

（法三）设获得总利润y＝0.2x＋0.4（50-x）＝-0.2x＋20.

因为-0.2＜0，y随x的增大而减少，

所以当x＝17时，获得利润最大，最大利润是：-0.2×17＋20＝16.6（万元）.

即生产A种产品17件，生产B种产品33件，获利最大，最大利润是16.6万元.

点评：本题考查了利用一元一次不等式组来解决最优方案问题，解题的关键是根据题意列出不等式组.解答这类问题，要正确地将实际问题转化为不等式组数学模型，得到切实可行的解题策略，并将求出的不同结果转化为具有现实意义的各种方案进行选择，最终确定最佳方案.本题综合考查学生的阅读能力、分析推理能力和数学建模思想.