变截面臂架腰绳系统优化
2012-07-25高顺德孙吉产
高顺德,周 杨,孙吉产,王 欣
(1.大连理工大学 机械工程学院,辽宁 大连 116024;2.中石化集团 第十建设公司,山东 淄博 255000)
追求起重量的不断增大、工作幅度的扩大是起重机发展的必然趋势.为提高起重量,扩大作业幅度,同时减少臂架的自重,重轻组合臂架是一种行之有效的组合结构,在许多大臂长臂架中都得到了应用.这种臂架较之以往统一规格的臂架,自重较轻,从倾覆稳定性角度更易实现自起臂.但由于自重轻,截面小,尤其是轻型臂,臂架整体刚度弱,易产生较大变形.而较大变形通常发生在重轻臂节过渡处,此处还易产生应力集中,是起臂过程中的危险截面.
目前,大多数结构的有限元分析都采用商用软件来完成.这种计算固然准确,但建模时间较长,计算过程会花费大量的时间与精力.因此研究在满足精度前提下的简化计算方法势在必行.对于细长梁结构,主要影响其吊载能力的是稳定性因素[1],较早期的有针对刚度进行的等效[2],但是其适用范围太小.现在较常采用的方法为等效惯性矩法,可以根据位移比较得到惯性矩等效公式[3],也可使结构长细比相等,求得惯性矩等效公式[4].
对于结构优化则可以分为尺寸优化、形状优化以及拓扑优化[5],利用不同优化方法对桁架结构进行优化的研究也有很多,有利用蚁群算法对桁架结构进行的优化[6],也有利用粒子群算法进行的尺寸优化[7].同时随着计算机技术的发展,也出现了利用商用有限元软件中的优化方法对结构进行的优化[8].
本文在相关文献理论和方法的基础上,进行深入研究,提出了针对变截面臂架的由建模到优化的一套完整的腰绳系统优化方法.针对具有明显变截面结构特征的臂架系统,特别是重轻组合臂架,就需要在简化时对变截面进行合理处理,以最大程度保留变截面结构的几何特征;本文利用等效惯性矩法,将格构式臂架等效成变截面梁结构,而且鉴于带腰绳的臂架系统呈现出了比较明显的几何非线性特征[9],故采用二次加载[10]的方法进行计算;同时将有限元软件的零阶、一阶优化方法与其有机结合,实现优化;最后通过优化结果的对比分析,表明此种建模、优化方法的合理性与可行性.
1 变截面臂架系统的简化
由于格构式结构抗剪能力弱,则必须考虑剪力对其稳定性的影响.而剪力主要是由腹杆来承担,所以在计算等效惯性矩时必须考虑腹杆对其的影响.如前所述,关于惯性矩等效的方法较多,由于本文优化的目标与位移有关,所以选择利用位移比较得出的惯性矩等效公式为


由于过渡臂节是变截面臂架,所以在对其简化时需要分别对臂节两端的截面分别进行等效,等效成箱型结构,如图1所示,两端的截面高度与宽度分别是hx1,hy1和hx2,hy2.为使结构协调,中间截面的尺寸由两端截面唯一确定.简化后的结构如图2所示.

图1 过渡臂节截面尺寸图Fig.1 Dimensions of sections of tansitional boom
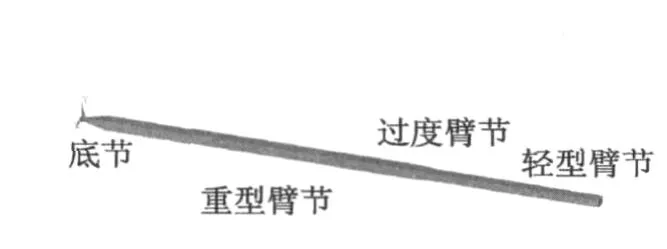
图2 简化后的有限元结构图Fig.2 Simple finite element model of boom
2 臂架系统的优化方法
利用ANSYS优化模块,以参数化模型描述整个优化分析过程,从而实现可变参数的有限元优化设计[11].
2.1 确定变量

2.2 约束条件
对于设计变量D,γ,由于腰绳一般都设置在过渡臂节前后,由此可以确定D的约束范围;在起臂、吊载工况下,拉板与臂架的夹角γ的约束范围也可以根据具体工况给出.如图3所示,则D必须满足Dmin≤D≤Dmax的要求;γmax为前后拉板为一条直线时的拉板与臂架的夹角;γmin则为此臂长臂架在各种工况(包括起臂和工作工况)下,拉板和臂架之间最小角,由于臂架和拉板之间的夹角理论上可以无限小,所以γmin可设为0;则γ必须满足γmin≤γ≤γmax.
2.3 目标函数
挠度是衡量腰绳作用的主要指标之一,而且在分析中可以直接提取节点的位移从而求出臂架的整体下挠.腰绳最主要的作用是保证起臂工况下是臂架挠度不超过许用挠度,而且在吊载工况下臂架不会产生反弯.所以一根腰绳必须同时满足上述两种情况.鉴于此,特构造分段函数并采用臂架的挠度值作为腰绳系统优化的目标函数.
2.4 惩罚函数
由于在吊载工况下,带腰绳的臂架可能会产生反弯,这种反弯在优化过程中无法自动排除,所以需要引进其他方法进行区别.本文利用惩罚函数的方法[12],构造惩罚函数.在臂架产生反弯时进行惩罚,迫使设计域向着不反弯的方向搜索.
构造的惩罚函数具体如下:
式中:Fc为产生反弯时,对臂架挠度进行惩罚后的计算结果;丨f0丨为求函数f0的绝对值,f0为臂架在计算过程中的挠度值,反弯时为正,正常下挠时为负;引入惩罚因子设为1010.
2.5 数学模型
目标函数为minf=F(α,D)+Fc(α,D),F为正常工况下未产生反弯时的挠度,约束条件为s.t.γmin≤γ≤γmax;Dmin≤D≤Dmax;设计变量为γ,D.
ANSYS的优化方法可分为一阶方法和零阶方法,也被称为间接方法和直接方法.其中一阶方法使用设计变量和目标函数的一阶偏导数,在每次迭代中梯度计算确定搜索方向.由于该方法在每次迭代中要产生一系列的子迭代,它所占用的时间较多,计算精度要高.这种方法精度很高,尤其是在因变量变化很大,设计空间也相对较大时,但是其最优解的求解与初始值的选取有关,所以只能保证取得局部最优解;零阶方法是一种相对比较完善的方法,是对所有状态变量和目标函数的逼近,通过调整设计变量的值,采用曲线拟合的方法去逼近状态变量和目标函数,该方法适合于大多数工程问题[13].为保证求解精度,本文首先采用零阶方法中的随机序列法产生随机序列组,在其中找到最优序列,将此序列作为初始值,代入一阶方法中进行子迭代,以求得最优解.具体优化流程如图4所示.
由于重轻组合臂架臂长较长,所以具有明显的几何非线性特征,这种特性在计算中必须被考虑进去.而且考虑到臂架在起臂、工作过程中产生二次变形,所以在进行迭代计算时采用二次加载的方法处理,以期能够使所求的挠度值与实际情况接近,达到更好的优化效果.
3 实例分析
本文中采用660t履带起重机的120m臂架,因为起臂和最小幅度两种工况对于腰绳的长度和位置影响最为明显:起臂工况中,臂架平铺在地面上,此时由于重力而产生的下挠较为明显,增加腰绳可有效减少挠度;最小幅度工况下,臂架受轴向力影响较大,中间臂节受到腰绳拉力影响,极易产生反弯.所以案例分析中选用此两种工况作为确定腰绳长度和位置的迭代工况.
120mm臂架具体参数为臂节长度L1=6mm,L2=71mm,L3=6mm,L4=37mm;拉板铰点位置x=18 299mm,y=26 605mm;重型臂节截面尺寸hx1=2 750mm,hy1=2 600mm;轻型臂节截面尺寸hx2=2 300mm,hy2=2 100 mm;臂架自重为73t;最小幅度起重量为124t,拉板横截面积为2 600mm2.根据式(1)、式(2),所计算出的等效惯性矩见表1.
设定初始设计变量:γ=0.12rad(0.004rad≤γ≤0.19rad),D=37 000mm(33 000mm≤D≤39 000mm).

表1 臂节等效惯性矩Tab.1 Equivalent inertia moments mm4
首先利用随机法,对此带腰绳臂架进行计算迭代,搜索出优化初值.所求得最后结果如表2所示.

由表2—表4可以看出,在不反弯的前提下,前拉板与臂架之间的夹角很大程度上决定了臂架的挠度,随着夹角的增大,挠度也在增大;夹角小到一定程度时会导致臂架的反弯.这是由于拉板与臂架的夹角直接决定了腰绳的长度,而腰绳的长度直接决定了臂架的挠度与是否反弯.这与实际情况相符;当前拉板与臂架夹角相差无几时,腰绳挂点距臂头的距离就会决定腰绳的长度,距离越短,腰绳长度越小,从而臂架的下挠程度也越小(由表2中第4,28行可以看出).

表2 随机法优化结果Tab.2 Result for random iterations

表3 一阶优化方法结果Tab.3 Result stemmed from first-order method

图5 最优情况下臂架位移图Fig.5 Displacement of boom in optimized case
如表2—表4所示,分别利用不同的方法进行优化,所求的结果略有差异.为保证优化后结果最优,采用本文中所提出的方法,即首先利用随机法生成较优序列,将此序列作为初始值代入一阶优化方法中进行子迭代,即:首先设定变量初始值γ=0.12rad,D=37 000mm,利用随机法优化的结果挠度为1 182.1mm,然后将此时的最优序列γ=0.143 95rad,D=37 756 mm作为初始值赋给设计变量,运用一阶优化方法优化得到结果为1 178.3mm,具体见表5所示.

表4 各部件受力Tab.4 Load for every part kN

表5 最优挠度值Tab.5 Optimal value
4 结论
本文通过现有的等效惯性矩方法,对臂架模型进行简化,对简化后的变截面实腹梁模型进行分析,可以在保证计算精度的同时节约计算时间,避免计算过程发散.利用APDL(ANSYS Parametric Design Lang uage)对简化后的实腹梁建模,在计算过程中考虑了臂架的二次变形效应,优化过程中直接调用了ANSYS的优化模块,使整个建模、分析、优化过程考虑因素完整,符合实际工作状况,而且避免了手动计算臂架挠度的繁琐,也不需要设计者编写大量优化算法即可得出较优的腰绳长度,为腰绳系统设计提供了一种可行的设计方法.
[1]DRAZUMERIC R,KOSEL F.Optimization of geometry for lateral buckling process of a cantilever beam in the elastic region[J].Thin-Walled Structures,2005,43:515-529.
[2]吴亚平.变截面压杆稳定性计算的等效刚度法[J].力学与实践,1994,16(1):58-60.
WU Yaping.Equivalent stiffness method to stability computation of non-uniform section pressure beam[J].Mechanics and Practise,1994,16(1):58-60.
[3]陆念力,王佳,兰朋.格构式构件整体稳定性分析的等效惯性矩法[J].建筑机械,2008,8(8):79-84.
LU Nianli,WANG Jia,LAN Peng.Equivalent inertia moment method to the overall stability analyse of lattice type beam[J].Construction Machinery,2008,8(8):79-84.
[4]王欣,马青,滕儒民,等.基于ANSYS的履带起重机臂架弹性稳定性计算的简化模型研究[J].起重运输机械,2009(11):15-19.
WANG Xin,MA Qing,TENG Rumin,et al.Elastic stability analysis of crawler crane boom system based on ANSYS[J].Hoisting &Conveying Machinery,2009(11):15-19.
[5]SU R,WANG X,GUI L,et al.Multi-objective topology and sizing optimization of truss structures based on adaptive multi-island search strategy[J].Struct Multidisc Optim,2011,43:275-286.
[6]LUH G,LIN C.Optimal design of truss structures using ant algorithm[J].Struct Multidisc Optim,2008,36:365-379.
[7]SCHUUTE J,GROENWOOD A.Sizing design of truss structures using particle swarms[J].Struct Multidisc Optim,2003,25:261-269.
[8]SONG Shijun,LI Lei,WANG Jiyong,et al.APDL language-based optimization of tower crane[C]∥International Conference on Digital Manufacturing & Automation.New Jersey:IEEE-CPS,2010:248-251.
[9]ZIENKIEWICZ O,TAYLOR R.The finite element method for solid and structural mechanics[M].Singapore:Elsevier Pte Ltd.,1998.
[10]王欣,辛宏彦,孙丽.基于有限元的腰绳系统设计方法[J].中国工程机械学报,2005,4(4):452-455.
WANG Xin,XIN Hongyan,SUN Li.Auxiliary bracing’s arithmetic based on finite element method[J].Chinese Journal of Construction Machinery,2005,4(4):452-455.
[11]龚曙光,谢桂兰.ANSYS操作命令与参数化编程[M].北京:机械工业出版社,2004.
GONG Shuguang,XIE Guilan.ANSYS and parametric programme[M].Beijing:China Machine Press,2004.
[12]唐焕文,秦学志.实用最优化方法[M].大连:大连理工大学出版社,2004.
TANG Huanwen,QIN Xuezhi.Paractical methods of optimization[M].Dalian:Dalian University of Technology Press,2004.
[13]余联庆,梅顺齐,杜利珍,等.ANSYS在结构优化设计中的应用[J].中国水运,2007,3(3):76-77.
YU Lianqing,MEI Shunqi,DU Lizhen,et al.The application of ANSYS in structural design[J].China Water Transport,2007,3(3):76-77.
