行波超声波电动机混沌建模与分析

李文娟，史敬灼

(河南科技大学，河南洛阳471003)

0 引 言

混沌是一类典型的非线性运行状态，普遍存在于鼠笼式异步电动机、同步磁阻电动机、无刷直流电动机等电磁电机驱动控制系统中。对电机系统的混沌运行进行研究，从一个新的角度认识这一非线性现象，有助于维持电机系统的稳定运行，亦可为混沌运动控制提供必要基础。

作为一种基于逆压电效应实现机电能量转换的特种电机，超声波电动机的运行机理完全不同于传统的电磁电机，并具有一些独特的性能特点，这使它不仅已经应用于家用电子、微型机器人、航天等领域，而且在其它众多运动控制领域有着广阔的应用前景。由于包含压电能量转换、摩擦能量传递等非线性过程，超声波电动机表现出强非线性和强耦合性。文献［1］的研究已验证了超声波电动机中存在混沌行为。为了分析超声波电动机本身的混沌特性，确定其混沌区域，从而抑制电机的混沌行为，还需要建立一个能够用来对超声波电动机混沌运行状态进行分析的电机模型。

本文针对Shinsei USR60型行波超声波电动机，采用自制的驱动控制电路，分析了超声波电动机系统的混沌运行状态。为了分析超声波电动机系统是否存在混沌特性，本文根据理论分析建立了超声波电动机转速控制系统的混沌分析模型，调节电压幅值－转速控制器参数来研究超声波电动机的运行特性。通过仿真，获得了电机转速相对于控制参数的Lyapunov指数谱、分岔图及电压相对于转速的轨迹图，结果表明行波超声波电动机在一定工作情况下将呈现出混沌运动，并给出了混沌运动区域对应的控制参数取值范围。

1 行波超声波电动机的混沌分析模型

超声波电动机的运行涉及两部分相互联系的能量转换过程。一是在电机定子内部，由压电陶瓷利用逆压电效应将外加电能激励转换为定子的微幅机械振动;二是在定子和转子的接触面上，利用摩擦作用将定子表面质点振动的机械能转换为转子的旋转运动。因此，相互作用的定子振动模型和定、转子接触模型是超声波电动机非线性模型的两个主要环节。

超声波电动机的基本动力学模型［2］:

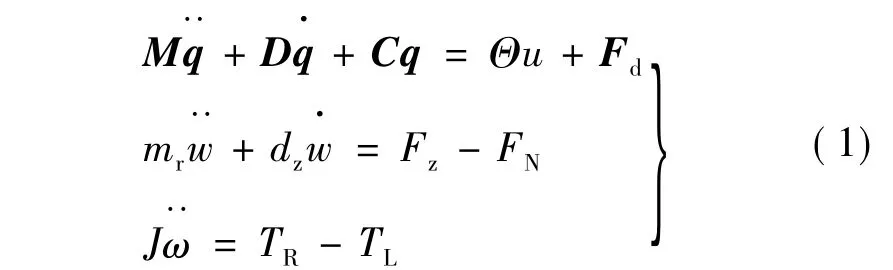
式中:M为定子模态质量矩阵;D为定子振动阻尼矩阵;C为模态刚度矩阵;q为定子模态坐标矩阵;mr为转子质量;w为定子表面到中性层的距离;Fz为定子对转子的轴向压力;FN为预压力，dz为电机轴向阻尼系数;ω为转子角速度;TR为输出转矩;TL为负载力矩;J为转动惯量。Fd为转子对定子的模态力矩阵:

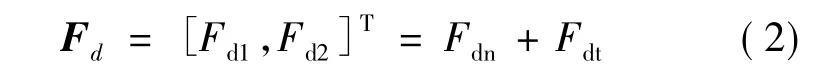
式中:Fdn为转子对定子的法向模态力;Fdt为转子对定子的切向模态力。

由于超声波电动机具有强耦合性，定子对转子产生作用力的同时，转子也会产生对定子的作用力，下面来计算转子对定子的模态力矩阵Fd。令:

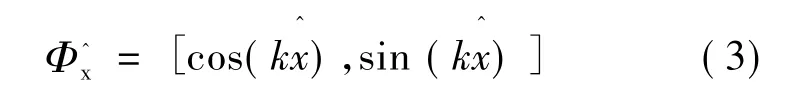
则转子对定子的法向模态压力:

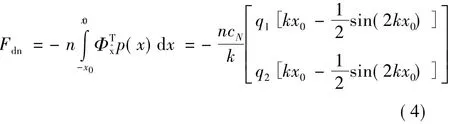
转子对定子的切向模态压力:

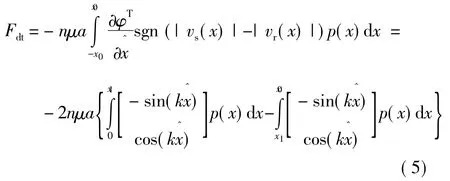
令:

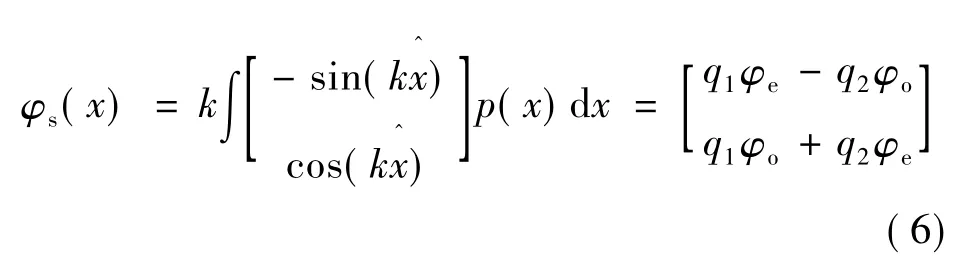
式中

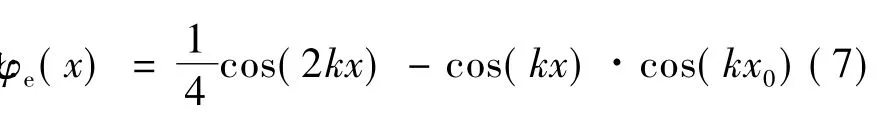
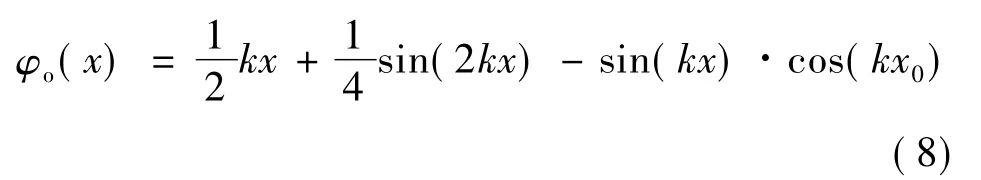
将式(6)、式(7)、式(8)代入式(5)，得:

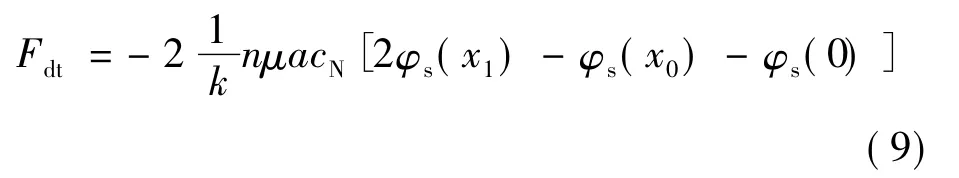
由式(2)、式(4)、式(5)，得:

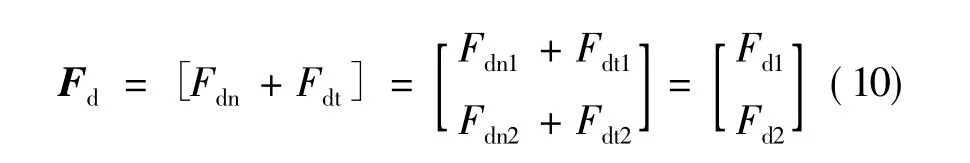
至此，建立起了超声波电动机的混沌分析模型，编写程序就可实现仿真计算。由于超声波电动机工作频率高，计算中取步长为1×10－6s。

2 行波超声波电动机转速控制系统混沌分析

本文对图1的转速控制系统进行混沌分析。超声波电动机有驱动电压幅值、频率、相位差等三个可控变量。考虑到改变频率可得到较宽的调速范围，而改变电压幅值能得到较高的调速精度，但调速范围有限，该系统采用频率和电压幅值两个控制变量对转速进行控制，设计了两个可互相切换的转速控制器。电压－转速控制器通过调节电压幅值来实现对转速的控制，用于转速误差较小情况下的精细调速，输出控制量为电压幅值的给定值;频率－转速控制器则以电机驱动频率为控制量，用来对转速进行大范围调节。为实现对电机两相驱动电压幅值的有效控制，图1系统还包含电压幅值闭环控制器，作为电压－转速控制的内环控制器。

图1 超声波电动机转速闭环控制结构框图

由于超声波电动机运行特性的限制，驱动电压幅值的调节存在上、下限值。超过上限值，电机定子压电陶瓷片可能损坏;低于下限值，电机会突然停转。图1中的“限幅”环节用来限制电压幅值的给定值在合理范围内。系统中，电压－转速控制器和频率－转速控制器均采用PI(比例积分)控制，电压幅值控制器为P(比例)控制［3］。电压幅值控制器输出为PWM占空比，通过PWM信号发生器给出PWM控制信号作用于H桥驱动电路，驱动电路实现逆变电压放大功能，输出高频高幅的驱动电压给超声波电动机。在仿真分析中，为了突出超声波电动机的运行特点，将PWM信号发生器和驱动电路等效为一个比例环节KD，与电压幅值控制器的比例环节KV一同并入转速PI控制器中的比例环节，于是得到系统仿真框图如图2所示。

图2中，频率－转速控制器与图1完全相同，输出为电机驱动频率值。仿真过程中，保持频率－转速控制器参数和电压－转速控制器的比例系数不变，调节电压－转速控制器积分系数KI进行转速阶跃响应仿真，得到不同KI时的电机驱动电压和转速变化波形。随后，采用互信息量法和Cao法计算延迟时间τ和最小嵌入维数m，进而用最小数据量法计算转速变化波形的最大Lyapunov指数［4］，得到转速相对KI的分岔图，并对系统的运动特性进行分析以确定其混沌区域。

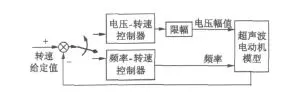
图2 超声波电动机转速控制系统仿真框图

在［1，20］范围内调节KI，仿真得到Lyapunov指数谱图和分岔图，如图3所示。由于在转速周期1行为过程中，一个周期内有两个极大值，所以在分岔图中表现出两个分支。表1给出了系统状态与KI取值之间的对应关系。图3中当 KI≤14.22时，Lyapunov指数均为负值，并且在分岔图中可以看出，该区域中转速表现为固定点和周期1运动。当KI＞18.2时，Lyapunov指数均为正数，系统表现出混沌行为，且转速波动幅度较大。而在14.22＜KI≤18.2区域中，Lyapunov指数主要为正数，但是存在Lyapunov指数为负数的小区域，如表1所示。

图3 转速相对于KI的分岔图及Lyapunov指数

表1 超声波电动机周期运动和混沌运动区域

这种现象反映出超声波电动机运动特性的复杂性。由于该区域中系统表现出周期行为的小区域比较分散且范围窄，所以在分岔图中该区域的周期行为不明显。

由表1 可知，在区域17.72 ＜KI≤18.2 内，超声波电动机转速表现为周期3运动。李天岩和Yorke J指出，只要3周期点存在，就有一切周期点存在，即周期3意味着混沌［5］。此观点进一步证明了超声波电动机运行过程中会表现出混沌特性。当KI=17.82时，输出电压峰峰值时域波形及相电压对于转速的轨迹如图4和图5所示。

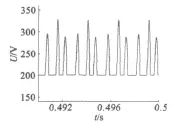
图4 KI=17.82 时，输出电压峰－峰值

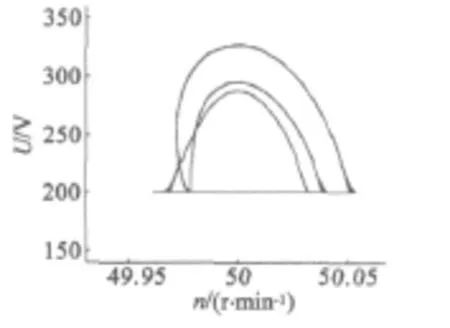
图5 KI=17.82 时，电压相对于转速的轨迹

图6和图7为KI=15.02时的仿真波形。很明显，转速、电压和转矩均出现了貌似随机而有界的不规则行为，电压相对转速的轨迹、正的Lyapunov指数和系统的分岔图均表明控制系统表现出了混沌行为。电机处于混沌状态时，转速限定在有限范围［49.92 r/min，50.07 r/min］之内，电压限定在［200 V，345 V］之内。

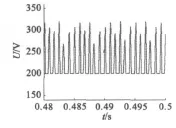
图6 KI=15.02 时，输出电压峰峰值

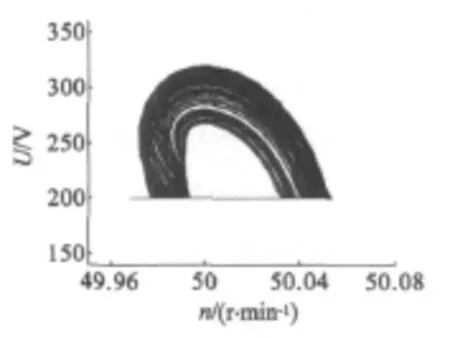
图7 KI=15.02 时，电压相对于转速的轨迹

3 结 语

本文根据超声波电动机的运行机理，通过理论分析，建立了超声波电动机转速控制系统的混沌分析模型。采用该模型对系统进行不同控制参数情况下的动态运行过程分析，表明了两相行波超声波电动机混沌运行的复杂性，这主要源于超声波电动机运行机理的复杂性。同时，给出了控制参数取值范围与混沌运动区域之间的对应关系，为进一步的混沌控制研究提供了必要基础。

［1］ 史敬灼，李文娟.基于相空间重构的两相行波超声波电机混沌运行分析［J］.微特电机，2011，39(3):14－16.

［2］ Mass J，Ide P，Frhleke N，et al.Simulation model for ultrasonic motors powered by resonant converters［C］//Conference Record of the 1995 IEEE Industry Applications Society 30th Annual Meeting.Orlando，USA，1995，3:111 －120.

［3］ 王海彦，史敬灼.基于CPLD的超声波电机H桥相移PWM控制［J］.电气自动化.2009，31(2):48－50.

［4］ 吕金虎，陆君安，陈士华.混沌时间序列分析及其应用［M］.武汉:武汉大学出版社，2002.

［5］ Li T Y，Yorke J A.Period three implies chaos［J］.The American Mathematical Monthly，1975，82(10):985－992.