一个力学问题的一对内力做功的探讨

何述平

（西北师范大学教育学院物理教育研究所，甘肃 兰州730070）

1 引言

质点系的一对内力做功与否对解决质点系问题至关重要，但就一对内力做功与否的论证存在欠严谨或令人费解甚至不合理，如下述典型力学问题中认为，m、M及水平面间无摩擦力，故机械能守恒；［1］m和M 的相互作用力具有相同的位移，做功之和为零，因此系统的机械能守恒.［2］那么，此力学问题的一对内力做功否？做的总功等于零否？怎样合理推证？解决此类问题的方法如何？本文就此进行相应的探讨，以期获得合理的解释，并为此类问题的解决提供物理学方法论的基础.

2 探讨

2.1 问题

如图1，质量为M、斜边长为L、倾角为θ的直角劈位于光滑水平面上，质量为m的小物块自光滑直角劈的顶部滑下，最初直角劈和小物块均处于静止状态.求小物块滑至直角劈底部时直角劈的速度大小，［1，2］小物块的速度和直角劈移动的距离.［3］

2.2 解析

为了明晰起见，采用隔离法解析此问题，且不局限于此题设问题，以获得关于此问题的尽可能完备的信息.

水平面为参照系（惯性系），分别以小物块、直角劈为研究对象，受力如图2.

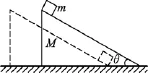
图1

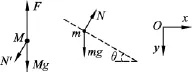
图2

在水平面沿水平x方向、竖直y方向建立坐标系O－xy.依据牛顿第二定律，分别对m、M有

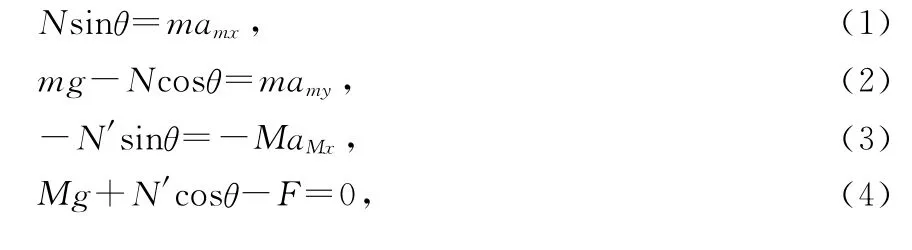
依据牛顿第三定律有（大小关系）

由（1）～（5）式知，m、M 应分别相对水平面做初速度为零的匀变速直线运动（x、y方向）.对m有

对M有

t为m自M 顶部滑至底部的时间，此时有位移大小关系

由（1）、（3）、（5）、（6）、（8）、（9）式得

（11）、（12）式分别为m自M 顶部滑至底部时的水平位移大小.

由（1）、（2）、（6）、（7）、（10）、（11）式得

此式表明弹性力N为恒力，再联系（1）～（5）式可佐证，m、M分别相对水平面做匀变速直线运动（x、y方向）.

由（1）～（5）、（13）式得

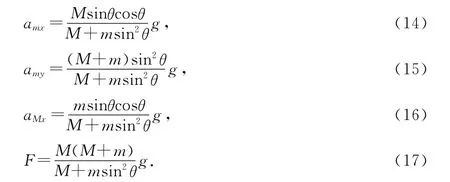
（13）、（14）、（16）、（17）式与运用动量守恒定律、非惯性系牛顿定律推得的结果［4］一致.（14）～（16）式再次表明，m、M分别相对水平面做匀变速直线运动（x，y方向）.对m有

对M有

由（10）～（12）式和（14）～（16）式及（18）～（20）式得

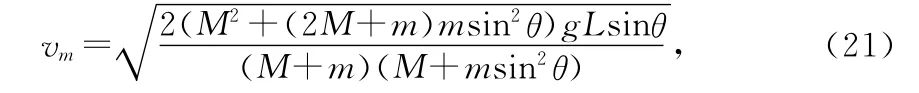
vm方向与水平面的夹角为

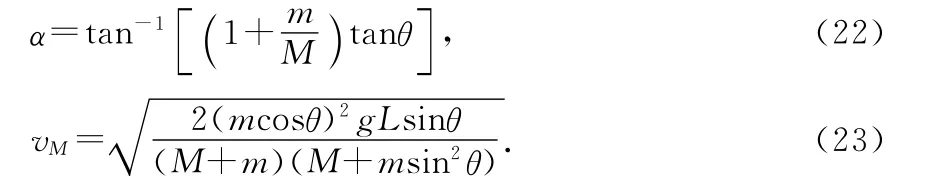
vM方向沿水平方向.（21）、（23）式分别为m自M 顶部滑至底部时的速度大小.

2.3 讨论

2.3.1 一对内力的功

由（10）～（12）式和（5）式可推证质点系（m＋M）的一对弹性内力N、N′做的总功等于零，即

Nsinθ·xm－Ncosθ·ym＋N′sinθ·xM＝0. （24）

由（9）、（10）式知，m对M 的相对位移与M 对m 的弹性力N正交，则由质点系一对内力做功的特点——一对内力做的总功仅决定于相互作用力和相对位移［3］知，一对弹性内力N、N′做的总功等于零.

由（21）、（23）式可验证系统（m＋M＋地球）的机械能守恒，即

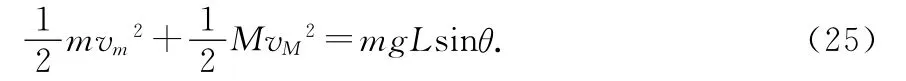
从而佐证系统的一对弹性内力N、N′做的总功等于零.

虽然一对弹性内力N、N′做的总功等于零，但由（24）式知，这对弹性内力却做了功，其效果是使系统的机械能发生了转化（m的重力势能转化为竖直方向m的动能和水平方向m、M的动能），从而使系统的机械能守恒.

2.3.2 释疑解惑

由（10）～（12）式知，m、M 分别相对水平面的位移大小不相等，由（9）、（10）式知，m相对M 的位移大小不为零.因此，认为m和M的相互作用力具有相同的位移、做功之和为零，［2］这是一种想当然的错误.

2.3.3 方法

一对弹性内力N、N′做的总功等于零，具有约束力的特点——约束力不做功，［5］因此，可将这对弹性内力视作质点系的内约束力，进而考虑运用机械能守恒定律解决问题.

设u为m相对M 的速度大小（方向沿直角劈的斜面向下），系统（m＋M）水平方向动量守恒，以水平面为参照系，m 运动方向为正向，有［1，2］

系统（m＋M＋地球）机械能守恒，有［1，2］

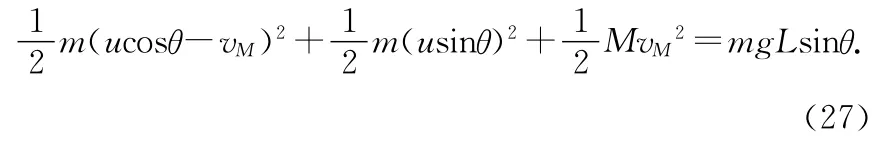
由（26）、（27）式得到与（21）～（23）式相同的结果；（26）式对0～t（m自M 顶部滑至底部的时间）积分，再结合（9）式，得同（11）、（12）式的结果.

比较上述隔离法和系统法知，隔离法虽有些繁琐，但解析透彻、过程清晰；而系统法不涉及物理过程的具体细节和质点间可能复杂的相互作用，直接考虑质点系的始末态物理量——动量、能量（状态量），因此，系统法具有简捷性.

鉴于上述，解决涉及质点系内力做功的力学问题时，应首先依据质点系一对内力做功的特点［3］定性判定一对内力做功与否；其次依据所要解决问题的性质运用隔离法或系统法或两者的有机结合进行定量推演.

另外，若从中学物理层次仅仅求此题设问题的水平位移大小，［6，7］则其合理方法之一如下.系统（m＋M）水平方向动量守恒，以水平面为参照系、m运动方向为正向，对m自M顶部滑至底部时的状态有

且有位移大小关系式（9）；再依据m、M分别相对水平面做初速度为零的匀变速直线运动，则位移大小为

t为m 自M 顶部滑至底部的时间.由（28）、（9）、（29）、（30）式可得同（11）、（12）式的结果.

3 结语

本文就一个典型力学问题的一对内力做功的问题进行了详细的探讨，不仅从功与能两个层次合理推证了质点系中质点间有相对运动时一对弹性内力做的总功等于零，功的层次上又给出了概念性和特点性的两个等效的推证方法；而且分别运用隔离法细致地和系统法简捷地分析解决了问题，比较了这两种方法的优劣，为依据问题的性质便捷地选择方法提供了根据；同时指明了推证此典型力学问题的一对内力做的总功等于零的不合理性，并提出了解决涉及质点系内力做功的力学问题的一般方法.本文不仅从大学普通物理层次细致地解析了此典型力学问题，而且给出了仅仅求解此问题的水平位移大小的中学物理的合理方法之一.

1 恽瑛，朱君哲，舒素珍.哈里德物理学习题解答（第1卷）.北京：科学出版社，1985.207－208

2 胡盘新，孙迺疆.普通物理学（第5版）习题分析与解答.北京：高等教育出版社，2003.83－84

3 漆安慎，杜婵英.力学基础.北京：高等教育出版社，1982.182，195－196

4 谢宝田，周友明，冯麟保.理论力学教程习题解.北京：中国科学技术出版社，1991.89－91

5 Kleppner D，Kolenkow R J.力学引论.宁远源等译.北京：人民教育出版社，1980.196

6 刘炳升.走进高中新课改：物理教师必读.南京：南京师范大学出版社，2005.150

7 陈刚.物理教学设计.上海：华东师范大学出版社，2009.145