高中物理模型教学中存在的若干问题
2012-07-19翁以忠
翁以忠
(江苏省泗阳中学,江苏 泗阳 223700)
物理模型的构建可以帮助学生对型异质同的问题迅速找出解题思路,摆脱情境的干扰,很快抓住问题的关键,从而提高解题的效率.但在实际教学中如果忽略对模型内涵的深刻理解,往往会带来负面效应,产生思维僵化,容易使人不注意题中条件的变化而套用已有的物理模型得出错误的结论.这一问题暴露出物理模型教学中的一些弊端,也引发了笔者的深刻反思.对存在的问题就以下几个方面进行探讨:
1 套用模型,知识迁移不恰当
例1.如图1所示,“翻滚过山车”是一种在离心轨道上运动的娱乐设施,有一列长为L的无动力列车,以初速度v0进入半径为R的离心轨道,若列车总长度超过数只圆轨道的周长,且轨道是光滑,则v0至少为多大才能保证列车顺利通过轨道的最高点?
参考答案:当过山车充满圆轨道时速度最小,此时在最高点速度应满足,由机械能守恒定律得
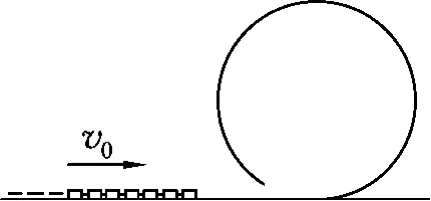
图1
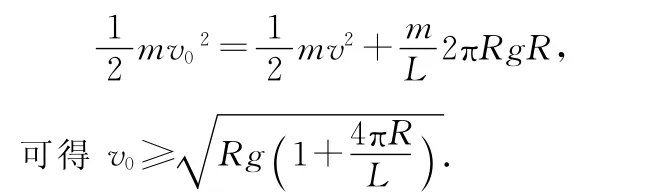
分析:本题套用了质点在竖直平面内圆形轨道中作圆周运动的运动规律,但这种迁移是不恰当的.原因在于一个孤立的质点在竖直轨道内运动时临界点在最高点,且只有重力提供向心力,而过山车充满圆形轨道后临界点也在最高点,但最高点的那部分不是孤立的,而是与两侧都有张力作用,所以向心力的最小值除了重力之外,还有张力也提供向心力.
当过山车充满竖直轨道后速度最小,且在离开轨道前作匀速圆周运动,选圆形轨道上一小段为研究对象,如图2,切线方向合力为0,T为张力,则有
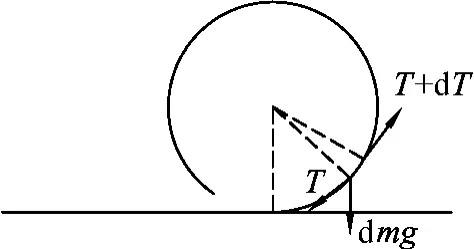
图2

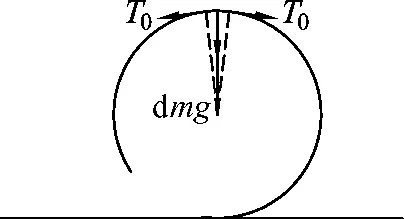
图3
T0=(T0为最高点的张力)
选最高点一小段为研究对象,如图3,此时轨道的弹力为0,则有

又根据机械能守恒定律有


2 忽视细节,模型建构不合理
所以,过山车要能顺利通过轨道最高点,需满足
例2.如图4所示,半径为R的圆弧形轨道的圆心在O点,在其最低点C附近的A处,由静止释放一个半径为r的均匀小球,小球将在ACB范围内来回滚动,则小球从释放起再次返回到A点所经历的时间为____________.
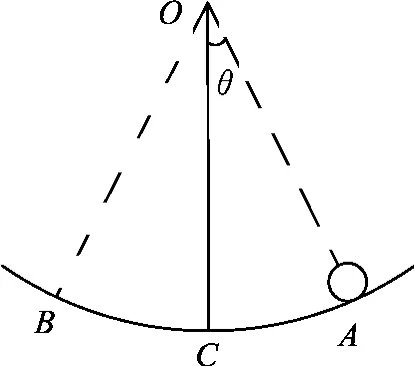
图4

分析:这是一道简谐运动中命制的习题.命制者的命题思路中误把相应的物理模型当作“单摆模型”.其实若圆弧光滑,小球在C点附近沿圆弧“滑动”而不是“滚动”,则相应的背景模型就可视为“单摆模型”,其周期应为


图5
但试题中小球是在圆弧ACB范围内滚动,故在滚动过程中应受到滚动摩擦力,其受力情况如图5所示.于是,在所谓“小角度”的近似条件下,相应的回复力可表达为
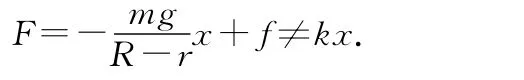
可见,以单摆为物理模型,得出了运动的周期是错误的.单摆在运动中不存在摆球的转动问题,而小球在轨道内来回滚动,这种情况下运动比较复杂,摩擦力和滚动对运动周期的影响不可忽视,通过以下计算来说明.
设小球离平衡位置的位移为x,小球球心与O的连线和竖直方向的最大夹角为θm,小球绕球心转过的角度为φ,在切线方向有
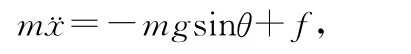
又有rφ=(R-r)(θm-θ),即

因为角度θ很小,故有sinθ≈θ.由上面各式可得
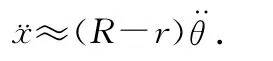

3 拼凑数据,题设条件不相容
例3.如图6所示,在光滑绝缘水平面上,一个半径r=0.1 m,电阻R=1Ω,质量m=0.1 kg的金属圆环,以v0=10m/s的速度滑向有理想边界的匀强磁场,磁场方向竖直向下,磁感应强度B=0.5T,在圆环的一半进入磁场的过程中,圆环内产生的焦耳热为Q=3.2J.求此时圆环的速度v、加速度a及圆环中感应电流的瞬时功率P.
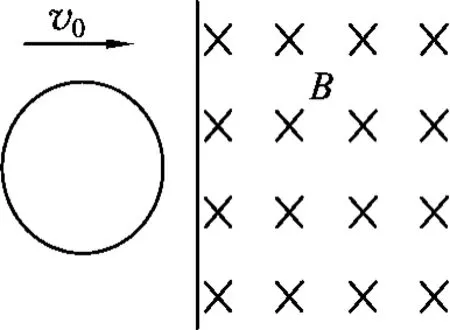
图6
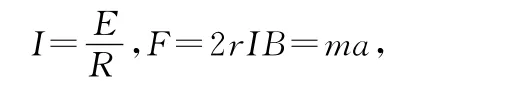
所以a=0.6m/s2.
由法拉第电磁感应定律得E=2rvB,又可得P=0.36W.
分析:这是一道在高中物理教学经常被引用的电磁感应中的变速问题.圆环进入磁场时切割磁感线的有效长度是从0逐渐增至2r,而圆环的速度则是从v0逐渐减至v.为了便于计算,使得圆环一半进入磁场时速度为整数,便凑出产生的焦耳热为3.2J.实际上当圆环一半进入磁场时所产生的焦耳热并不是这个数值,可通过下面计算来说明.
设圆环进入磁场中的长度AE为x,如图7所示.由几何知识有x=AE=r(1-cosθ),则
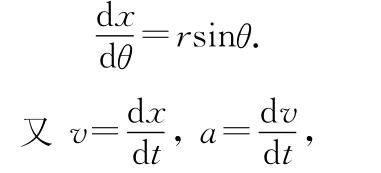
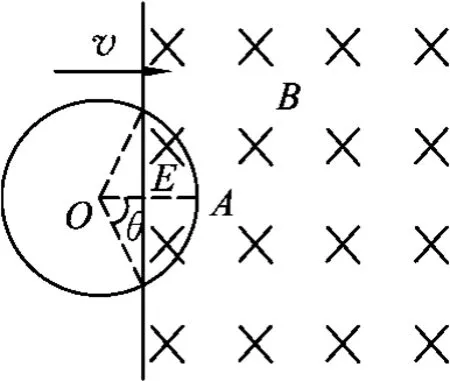
图7
根据法拉第电磁感应定律得
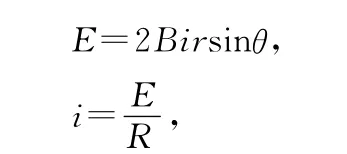
由牛顿第二定律知
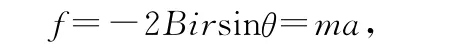
以上各式化简可得

根据能量守恒定律得

代入数据 Q=6.4×10-3J<3.2J.
可见,题中给出的焦耳热与题中的条件是不相容的,环中产生的焦耳热与磁场、圆环的电阻、圆环的开始速度及进入磁场中的长度密切相关.这种随便凑数据的做法在实际教学中经常出现,所造成的负面效应影响深远.它会让学生忽视对物理过程的分析,养成不注重事实的坏习惯.
4 缺乏比较,规律类比不正确
物块由细绳通过定滑轮拴在汽车上,如图8所示,车从A点由静止开始向左以加速度a做匀加速直线运动,当到达B位置时汽车的速度为v,则此时物块的速度和加速度分别为多少?
参考答案:通过矢量分解可得物块速度为v1=vcosθ,加速度为a1=acosθ
分析:题中对速度的分解是正确的,但对加速度分解是错误的.主要原因是把求解速度时所用的方法完全迁移到了求解加速度的问题中,将速度分解与加速度分解进行类比,认为既然沿绳子方向的速度大小是相同的,那么沿绳方向的加速度大小也是相同的.这种看法是有问题的.下面通过数学方法来说明:
由上面得v1=vcosθ,用微积分知识可得物块的加速度为
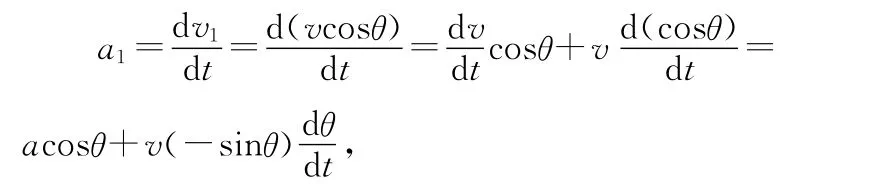
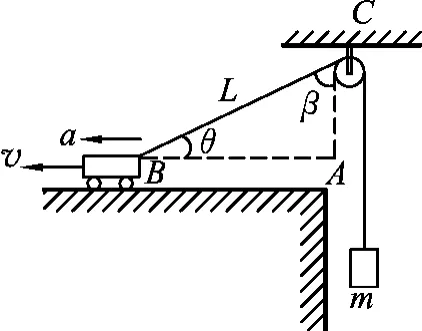
图8
式中ω为绳绕C点旋转的角速度.由速度分解知识可知,汽车在垂直绳子方向的速度分量为vsinθ,从而
将以上各式化简得

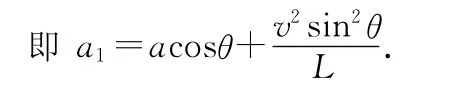
此式表明,物块的加速度不仅与a、θ有关,还与v、L有关.因加速度与速度的物理意义不同,所以二者分解时不能简单类比.
因此,在构建物理模型的教学过程中不能把它机械化,教条化、绝对化,因为任何物理问题都有其特殊性的一面.对待具体问题,一定要善于具体分析,不能简单的套用模型,生搬结论.只有这样才能对物理模型的应用得心应手.
