基于OpenFOAM的螺旋桨敞水性能预报方法

郑巢生 张志荣

中国船舶科学研究中心，江苏无锡214082

基于OpenFOAM的螺旋桨敞水性能预报方法

郑巢生 张志荣

中国船舶科学研究中心，江苏无锡214082

为深入研究螺旋桨周围的粘流问题，基于面向对象的开源CFD计算平台OpenFOAM，选择DTMB P4119桨作为对象，利用RANS方程计算了桨的敞水性能，并分别考察了网格依赖性和离散格式的影响。同时分析了不同半径处叶剖面的压力分布及桨前后的流场速度分布。为保证对流项离散的稳定性和高精度性，采用了二阶NVD格式Gamma混合差分格式，选取k－wSST模型作为湍流模型，压力速度耦合采用SIMPLE松弛算法。计算结果与试验数据吻合较好。研究建立了基于OpenFOAM的螺旋桨敞水性能预报方法。

粘流；螺旋桨；OpenFOAM；RANS；敞水性能；湍流模型

0 引 言

随着现代船舶性能的快速发展，能否准确预报螺旋桨性能至关重要。20世纪80年以来，基于RANS方程求解的粘流方法开始被广泛应用于模拟螺旋桨周围的粘流［1-2］。目前，国内进行螺旋桨方面的计算主要通过CFD商业软件Fluent和自编程序来实现，而OpenFOAM与前两者相比具有完全开源性、面向对象性和良好的继承性等优点。作为一款开源CFD计算平台，凭其灵活高效的C++模板自定义功能，OpenFOAM越来越受到CFD研究人员的关注。

本文基于OpenFOAM开源平台，将选用多参考系MRFSimpleFoam稳态求解器进行螺旋桨敞水性能预报方法的研究。

1 数值模拟

1.1 控制方程

在惯性参考系中，螺旋桨以设定的角速度绕固定轴旋转，流场是非定常的。因本文中只存在单一螺旋桨旋转，不存在定子的情况，所以既可以采用整个流场坐标建立在桨叶上的单一旋转坐标系SRF方法，也可以采用多参考系MRF方法建立N－S方程，即在桨叶附近区域采用建立在桨叶上的旋转参考系，在桨叶远场区域采用惯性参考系，再在两者交界面上通过将速度换算成绝对速度的形式进行流场数据交换。为便于今后考虑螺旋桨和定子同时存在的情况，本文采用MRF方法。

其惯性参考系下的N－S方程为：

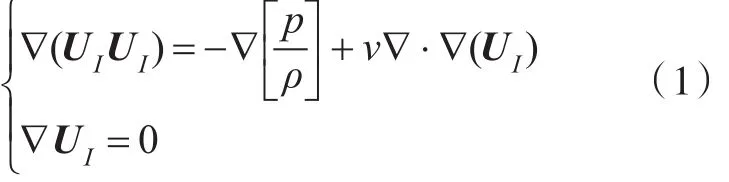
其旋转参考系下绝对速度形式的N-S方程［3］为：

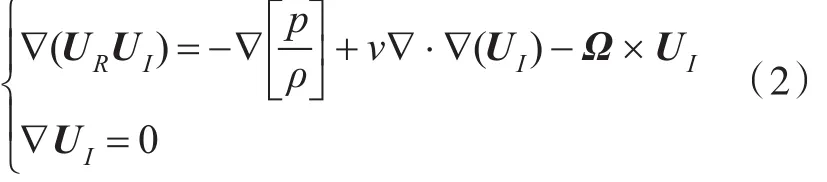
式中，UI和UR分别为绝对速度和相对速度；p为压力；ρ为密度；Ω为旋转角速度；Ω×UI为包含向心力的广义柯氏力项。

OpenFOAM中多参考系MRFSimpleFoam稳态求解器即根据式（2）求解旋转参考系下的绝对速度。

1.2 湍流模型

为了求解湍流应力项，引入了k－wSST湍流模型［4］，其中，湍动能k和涡量脉动强度w的输运方程为：

令 ϕ1表示常数 (α1，β1，σk1，σw1)，ϕ2表示常数(α2，β2，σk2，σw2)，ϕ 表示常数 (α，β，σk，σw)，它们之间关系为：

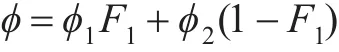
式中，α1=5/9；α2=0.44；β1=3/40；β2=0.082 8；σk1=0.85；σk2=1；σw1=0.5；σw2=0.856；β*=9/100。

1.3 离散方法

采用有限体积法求解任意多面体非结构网格离散下的RANS方程。选取的控制体单元如图1所示，图中P为控制体单元中心，N为邻近单元中心，f为单元界面。

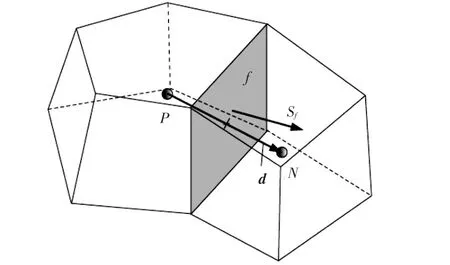
图1 有限体积离散Fig.1 The finite volume discretization

对流项在控制体上的积分和线性化如下：

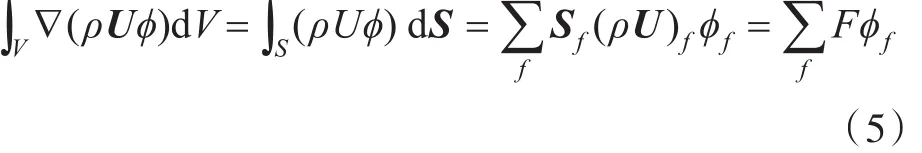
式中，面场ϕf采用Jasak提出的非结构网格下的Gamma混合差分格式：

通过权重系数γ混合二阶中心差分(ϕf)CD和一阶迎风差分(ϕf)CD，其表达式分别为：

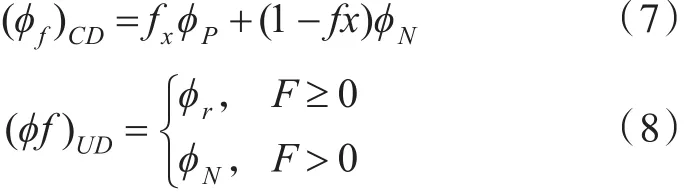
由文献［5］可知 γ∈（0 1），且由式（6）可知 γ越大，精度越高，但稳定性越差；γ越小，精度越低，但稳定性越好。本文中γ取值为0.2。

扩散项在控制体上的积分和线性化如下：

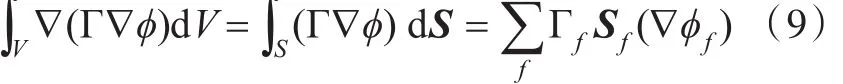
正交网格时，控制体单元中心P和N的位移向量d与平面 f正交，即平行于 Sf时，面梯度为隐式离散。

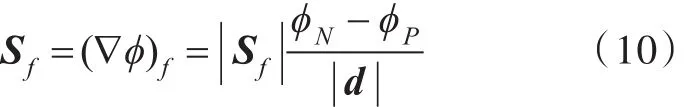
非正交网格时，先通过中心差分单元中心值得到单元中心梯度，再插值单元中心梯度引入显式补偿项。

在方程组求解过程中，压力与速度耦合采用SIMPLE松弛算法，其中 p，U，k和w的松弛因子分别为0.3，0.5，0.5和0.5。

1.4 几何模型

本文选取DTMB P4119桨作为计算对象。它是一个无倾斜、无纵倾的三叶桨，桨叶直径D＝0.314 8 m（图2）。

图2 DTMB P4119桨Fig.2 DTMB P4119 propeller

由于桨绕轴旋转具有周期性，因此文中采用的周期边界条件只需计算单桨流道，计算区域为如图3所示的1/3圆柱区域：上游入口位于桨前3.6D处，下游出口位于桨后5D处，侧边位于桨轴心3.8D处。

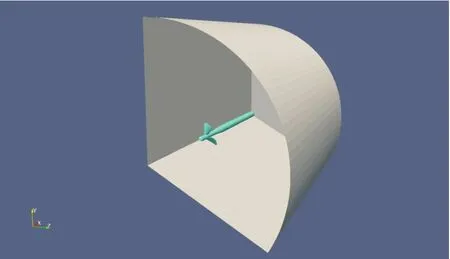
图3 计算区域Fig.3 Computational region

1.5 网格生成

由于采用多参考系，利用GAMBIT分块划分网格时，将旋转参考系下的区域划分为直径d＝1.08D，高h＝0.86D的1/3圆柱区域，采用非结构网格，并在桨叶表面均匀加密。惯性参考系下的区域采用结构网格，并向外逐渐稀疏。整个区域网格总数为1 086 986（图4）。

图4 分块网格划分Fig.4 Multi-block grid partition

为了方便OpenFOAM自动捕捉和处理滑移壁面及旋转边界条件，将旋转部分和固定部分分别命名为rotor和stator，然后再通过终端输入fluent⁃MeshToFoam即可。

1.6 边界条件

在OpenFOAM中，变量的初始化需要在每个以变量名命名的文本中进行，其初始化分别如下：

速度U ：入口为固定值U＝（5.078 0 0），出口为零梯度，桨叶、桨毂和侧边为固定值U＝（0 0 0）；

压力 p：入口为零梯度，出口为固定值 p＝0，桨叶、桨毂和侧边为零梯度；

湍动能 k：入口为固定值 k=3.87×10-5，出口为零梯度，桨叶、桨毂和侧边采用壁面函数；

涡量脉动强度w：入口为固定值w＝38.5，出口为零梯度，桨叶、桨毂和侧边采用壁面函数。

其中，湍动能k和涡量脉动强度w的初始值分别由湍流密度I和涡粘比 μt/μ得到。

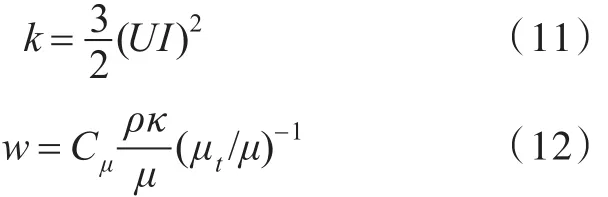
式中，I＝0.1%；μt/μ=1。

2 计算结果与分析

2.1 敞水性能

分别计算进速系数 J＝0.5，0.7，0.833，0.9和1.1工况下DTMB P4119桨的敞水性能，计算结果如图 5和表 1 所示，并与 Jessup［6］的试验结果相比较。其中：

式中，U为入口速度值；T和Q分别为桨推力值和扭矩值；ρ为密度；n为转速；D为螺旋桨直径。

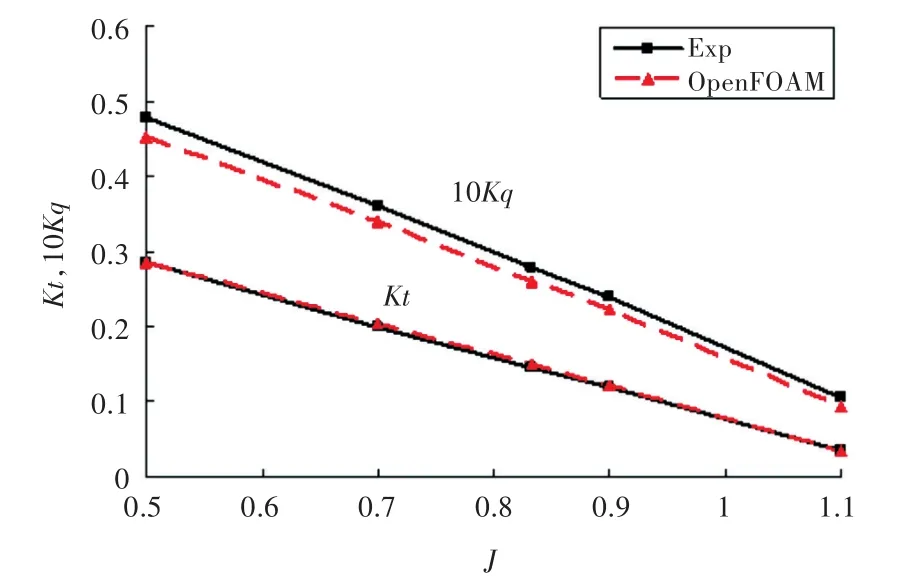
图5 DTMB P4119桨敞水性能曲线Fig.5 Open-water performance curves of DTMB P4119 propeller

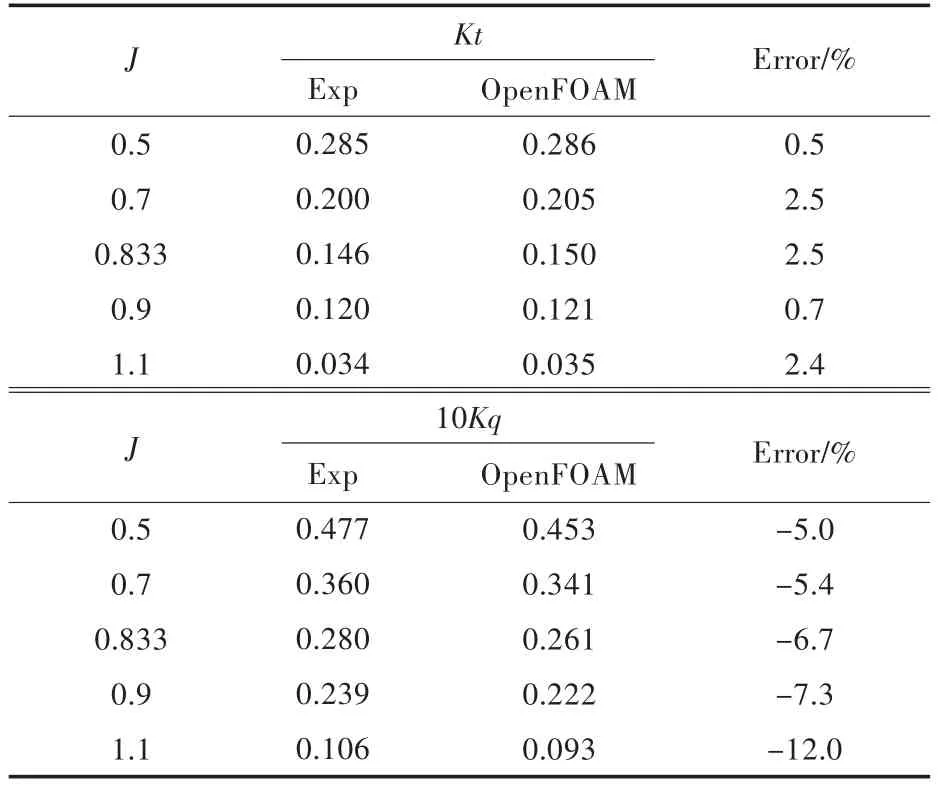
表1 DTMB P4119桨敞水性能比较Tab.1 Comparisons of the open-water performance of DTMB P4119 propeller

由图5可看出，OpenFOAM计算的桨的推力系数比实验值略大，而扭矩系数比试验结果略小一些。

从表1的具体数值看，推力系数与试验值的误差非常小，最大误差仅为2.5%，而扭矩系数与试验值的误差相对较大一些。造成较大误差的主要原因可能是混合差分格式中的权重系数γ取值较低，即应取较大的值，但同时还要兼顾计算的稳定性问题。

2.2 网格依赖性

为了研究网格的依赖性，选取更密的网格计算不同工况下的敞水性能（图6），即在桨叶表面加密，得到网格总数为1 614 109。计算表明，两种网格得到的结果几乎相同，但为了节省计算时间，本文将选取较粗的网格完成所有计算。

2.3 离散格式影响

为了研究离散格式的影响，选用一阶迎风格式计算不同工况下的敞水性能，并与试验值相比较。从图7可以看出，与Gamma格式相比，一阶迎风格式下的扭矩系数相对较小，而推力系数的误差则相对较大。

图6 网格依赖性比较Fig.6 Comparisons of grid dependence

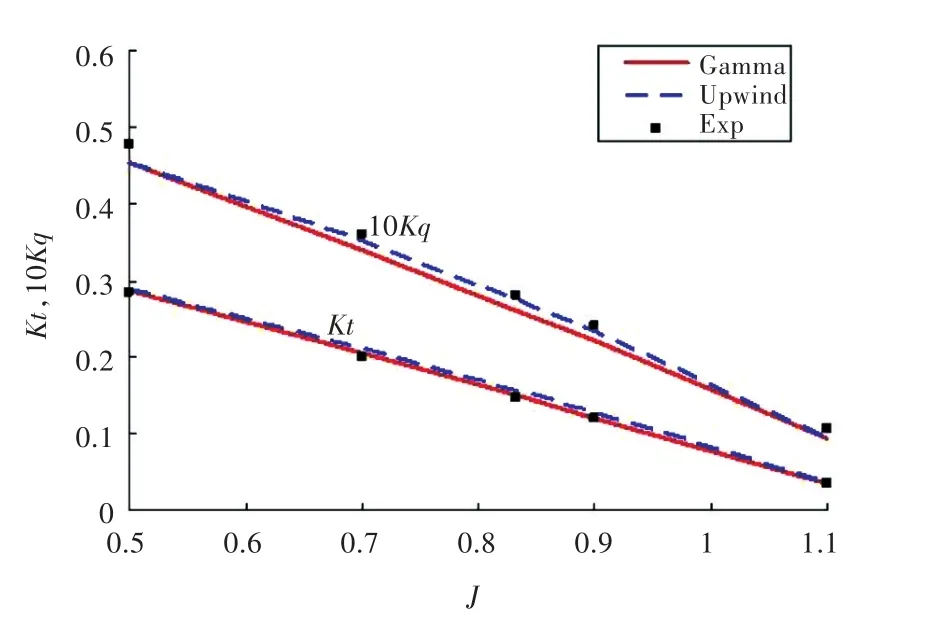
图7 离散格式比较Fig.7 Comparisons of discretization scheme

2.4 表面压力分布

Jessup利用LDV测量的速度场，通过伯努利方程换算得到不同半径上桨叶表面的压力分布。图8～图10分别给出了设计工况 J＝0.833时OpenFOAM计算得到的压力系数分布，并与经换算得到的结果进行了比较。图中，横坐标为x/C（x为叶剖面上的点沿弦长方向到导边的距离，C为叶剖面处弦长），纵坐标Cp为压力系数，定义如下：

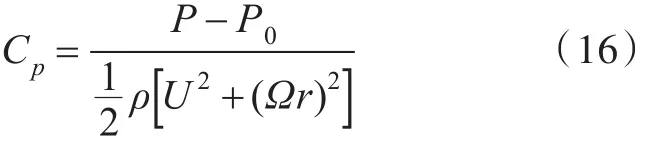
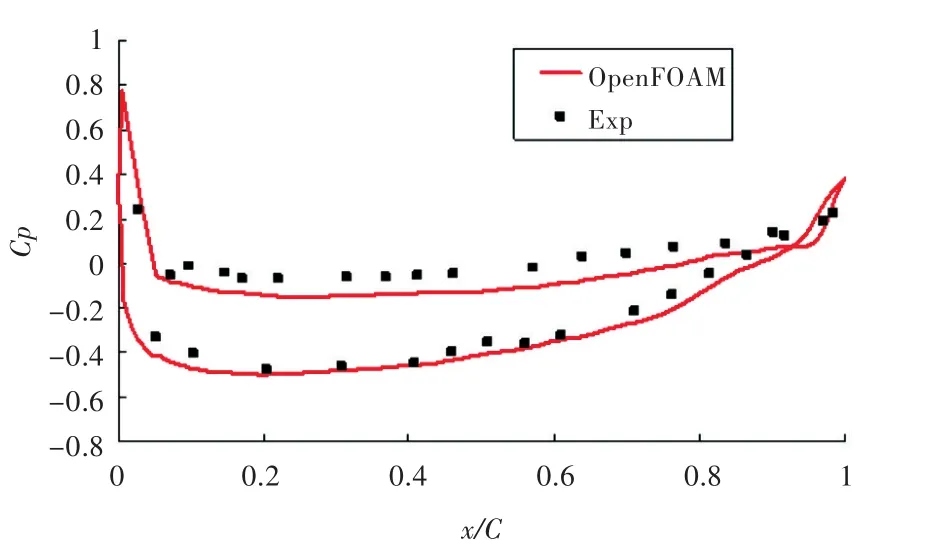
图8 r/R＝0.3处叶剖面压力系数分布Fig.8 Pressure coefficient distributions on blade section atr/R＝0.3

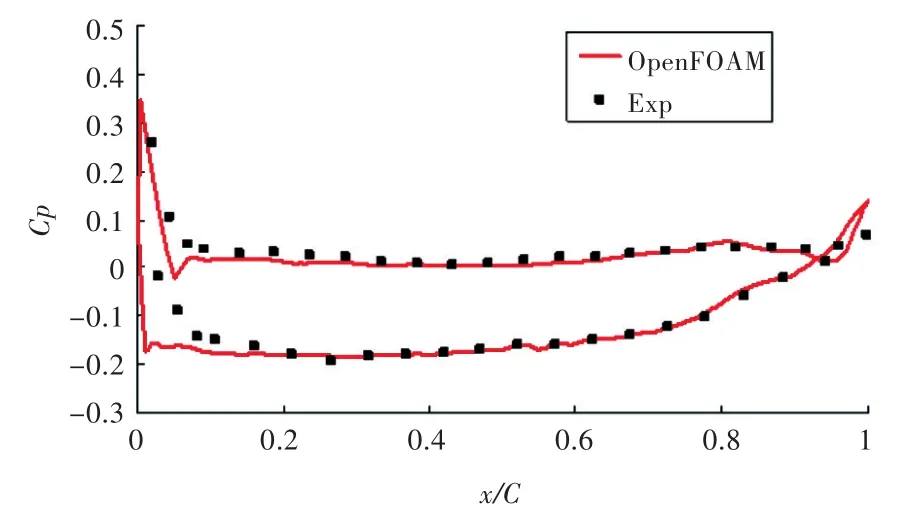
图9 r/R＝0.7处叶剖面压力系数分布Fig.9 Pressure coefficient distributions on blade section atr/R＝0.7

图10 r/R＝0.9处叶剖面压力系数分布Fig.10 Pressure coefficient distributions on blade section atr/R＝0.9

式中，P为静压；P0为远场参考压力；U为入口速度值；ρ为密度；Ω为旋转角速度值；r为叶剖面处半径。

由图8～图10可看出，OpenFOAM计算得到的不同半径叶剖面上的压力系数分布与Jessup的试验结果十分吻合，因此能准确预报推力系数和扭矩系数。经比较可以看出，导边附近的压力系数比试验值略小，这主要可能是由于导边附近的网格不够密。在叶根附近，r/R＝0.3处的叶剖面压力系数分布与Jessup的试验结果差别相对较大，这可能是因为Jessup在用伯努利方程换算时假设流体为理想流体，而没有考虑叶根处粘性及漩涡的影响。

2.5 流场分布

图11～图18分别给出了设计工况J＝0.833时桨盘面前方x＝-0.3R处和桨盘面后方x＝0.328 1R处轴向、径向和切向速度的周向平均分布。图中，横坐标为r/R，纵坐标用入口速度无量纲化：

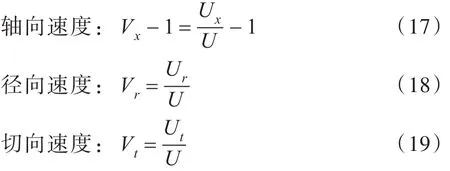
式中，U为入口速度值；Ux、Ur和Ut分别表示周向平均后的轴向、径向和切向速度值。

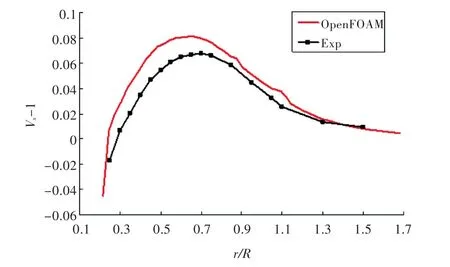
图11 桨盘面前x＝-0.3R处轴向速度的周向平均值Fig.11 Circumferentially-averaged value of axial velocity atx＝-0.3R

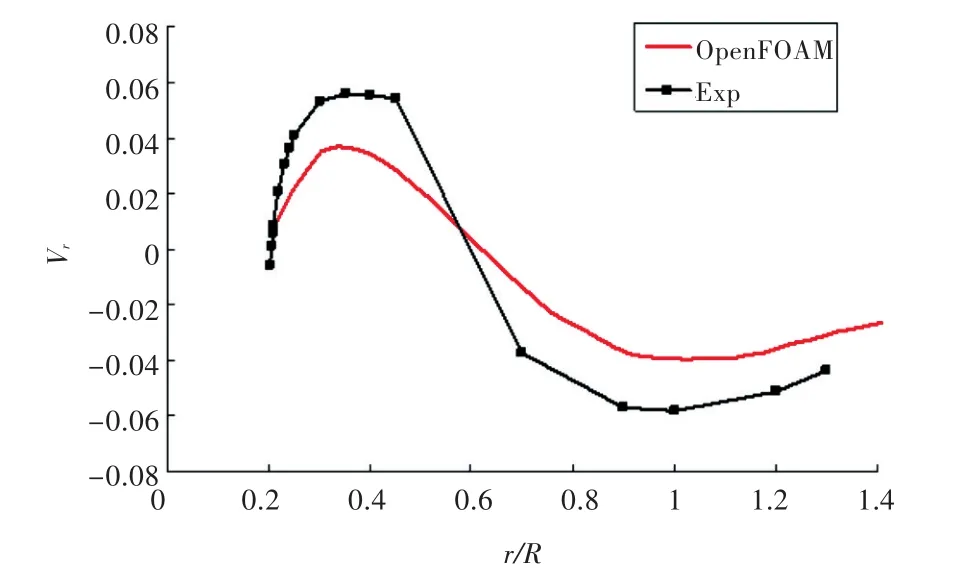
图12 桨盘面前x＝-0.3R处径向速度的周向平均值Fig.12 Circumferentially-averaged value of radial velocity atx＝-0.3R

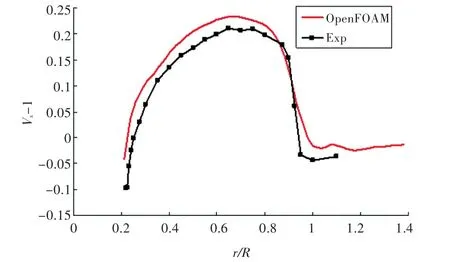
图13 桨盘面后x＝0.328 1R处轴向速度的周向平均值Fig.13 Circumferentially-averaged value of axial velocity atx＝0.328 1R

图14 桨盘面后x＝0.328 1R处径向速度的周向平均值Fig.14 Circumferentially-averaged value of radial velocity atx＝0.328 1R

图15 桨盘面后x＝0.328 1R处切向速度的周向平均值Fig.15 Circumferentially-averaged value of tangential velocity at x＝0.328 1R

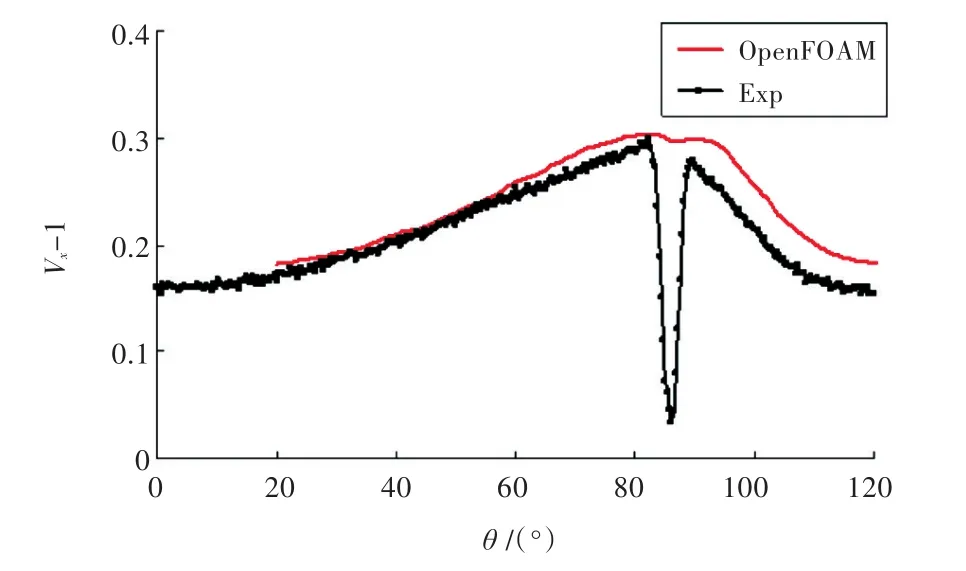
图16 桨盘面后x＝0.328 1R，r＝0.7R处轴向速度的周向分布Fig.16 Circumferential distributions of axial velocity at x＝0.328 1R，r＝0.7R

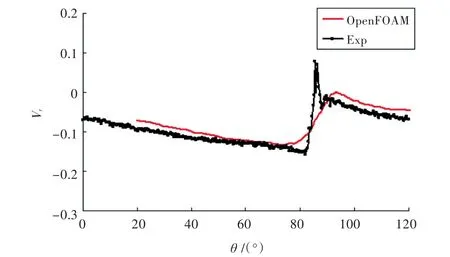
图17 桨盘面后x＝0.328 1R，r＝0.7R处径向速度的周向分布Fig.17 Circumferential distributions of radial velocity at x＝0.328 1R，r＝0.7R

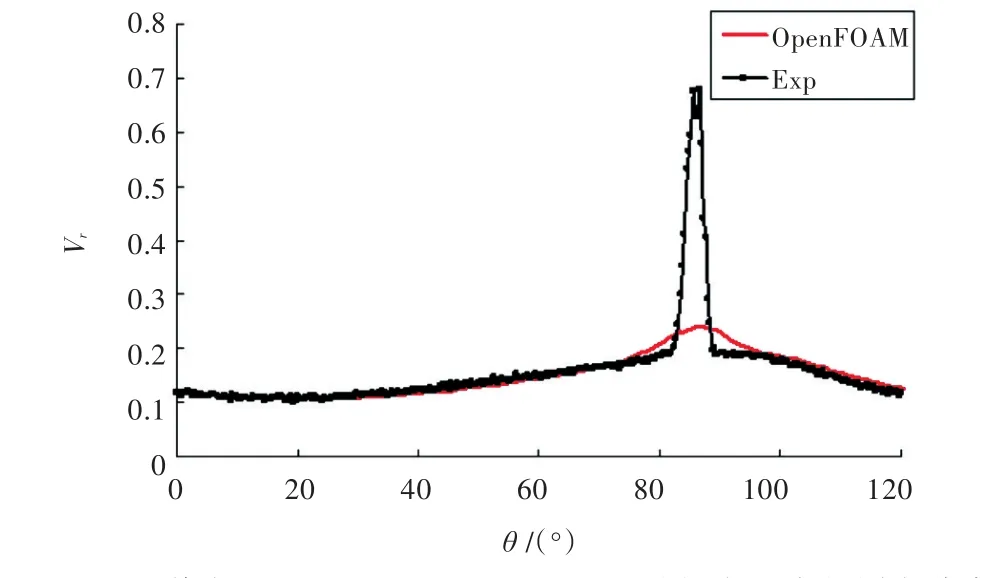
图18 桨盘面后x＝0.328 1R，r＝0.7R处切向速度的周向分布Fig.18 Circumferential distributions of tangential velocity at x＝0.328 1R，r＝0.7R

由图11～图15可看出，OpenFOAM计算得到的桨盘面前方 x＝-0.3R处及桨盘面后方 x＝0.328 1R处轴向速度和径向速度的分布与试验结果基本吻合。

图16～图18分别给出了桨盘面后方 x＝0.328 1R，r/R=0.7处轴向、径向和切向速度的周向分布。OpenFOAM的计算结果能较好地预报速度的变化趋势，但没有精确捕捉到速度峰值，这可能是由于此处网格不够密而导致数值耗散过大［7］。要捕捉峰值变化，可以通过试验测量到的伴流峰值分布，也可以根据势流方法中假设的尾涡模型，在相应的位置布置十分精细的网格。

3 结 语

本文基于开源CFD计算平台OpenFOAM，计算了不同工况下DTMB P4119桨的敞水性能、桨叶压力分布和流场速度分布，并考察了网格依赖性和离散格式的影响，计算结果与试验数据能很好地吻合，建立了基于OpenFOAM的螺旋桨敞水性能预报方法，为今后研究更复杂的粘流问题奠定了基础。

［1］TANG D H，CHEN J D，ZHOU W X.Comparative cal⁃culations of propeller performance by RANS/Panel Method［C］//22nd ITTC Propulsion Committee，Propel⁃ler RANS/Panel Method Workshop，Grenble，1998.

［2］CHEN J D，ZHOU W X，TANG D H，et al.Comparative calculations of unsteady propeller performance by pan⁃el method［C］//22nd ITTC Propulsion Committee，Pro⁃peller RANS/Panel Method Workshop，Grenble，1998.

［3］See the MRF development［EB/OL］.［2011-11-14］.http：//openfoamwiki.net.index.php.See_the_MRF_de⁃velopment.

［4］MENTER F R.Two-equation eddy-viscosity turbu⁃lence models for engineering applications［J］.AIAA Journal，1994，32（8）：1598-1605.

［5］JASAK H，WELLER H G，COSMAN A D.High resolu⁃tion NVD differencing schemes for arbitrarily unstruc⁃tured meshes［J］.International Journal for Numerical Methods in Fluids，1999，31：431-449.

［6］JESSUP S D.Experimental data for RANS calculations and comparisons［C］//22nd ITTC Propulsion Commit⁃tee，Propeller RANS/Panel Method Workshop，Gren⁃ble，1998.

［7］韦喜忠，黄振宇，洪方文.基于非结构网格的螺旋桨周围流场大涡模拟［J］.水动力学研究与进展，2008，23（4）：419-425.

WEI X Z，HUANG Z Y，HONG F W.Large eddy simu⁃lation of flow field about marine propeller on unstruc⁃tured meshes［J］.Chinese Journal of Hydrodynamics，2008，23（4）：419-425.

Prediction Method for Open-Water Performance of Propeller Based on OpenFOAM

ZHENG Chao-sheng ZHANG Zhi-rong

China Ship Scientific Research Center，Wuxi 214082，China

In order to further investigate the viscous flow around the propeller，open-water performance prediction of DTMB P4119 propeller was performed using RANS flow solver in OpenFOAM software.And the grid dependence and effects of discretization schemes were investigated.The pressure distributions on the blade sections at different radii and velocity distributions ahead and behind the propeller were also ana⁃lyzed.To ensure the stability and accuracy of convective term discretization，the approaches are as fol⁃lows：（a）adopting second order NVD Gamma blended differencing scheme；（b）using k－wSST model as the turbulence model；（c）applying the SIMPLE algorithm for pressure-velocity coupling.The predicted results agree well with the experimental data.

viscous flow；propeller；openFOAM；RANS；open water performance；turbulence model

U661.33

A

1673－3185（2012）03－30－06

10.3969/j.issn.1673－3185.2012.03.006

2011－11－14

郑巢生（1987－），男，硕士研究生。研究方向：计算流体力学。E⁃mail：zcszcs2005＠163.com

张志荣（1966－），男，博士，研究员。研究方向：计算流体力学。E⁃mail：zhangzr8＠public.wx.js.cn

张志荣。

［责任编辑：李勇群］